
- •Практикум решения задач по дисциплине «Системный анализ»
- •Решение задач Линейного программирования графическим методом
- •1.1 Задача 1
- •Задача 2
- •Задача 3
- •Задача 4
- •Задача 5
- •Задача 6
- •Решение задач Линейного программирования симплекс-методом
- •2.1 Алгоритм 1 Симплекс преобразования на основе укороченных симплекс таблиц
- •2.2 Алгоритм 2 Симплекс преобразования на основе укороченных симплекс таблиц
- •2.3 Алгоритм 3 Симплекс преобразования на основе укороченных симплекс таблиц для решения двойственной задачи Линейного программирования
- •2.4 Задача 1
- •2.5 Задача 2
- •2.6 Задача 3
- •2.7 Задача 4
- •Решение матричных игр 2 X n и m X 2 графоаналитическим методом
- •3.1 Задача 1 ( решение игры 2 X n)
- •3.2 Задача 2 ( решение игры m X 2)
- •3.3 Задача 3
-
Задача 6
Используя метод исключения переменных и геометрические построения, найти решение задачи Линейного Программирования:
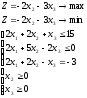
Решение
-
Из третьего ограничения
 можно выразить
можно выразить
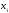 :
:

-
Подставим выражение для
 в первое ограничение
в первое ограничение
 :
:

-
Подставим выражение для
 во второе ограничение
во второе ограничение
 :
:
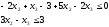
-
Таким образом, после применения метода исключения переменных от исходной задачи перейдем к задаче вида:
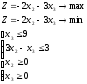
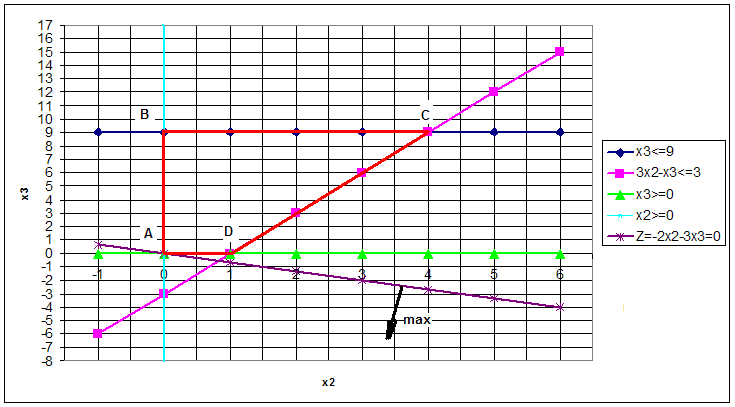
Данная задача может быть решена на плоскости графическим методом решения задач линейного программирования.
-
Необходимо на плоскости построить прямые, соответствующие заданным неравенствам.
Прямая, соответствующая неравенству
 ,
проходит через точку
,
проходит через точку
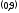 параллельно оси
параллельно оси
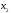
Прямая, соответствующая неравенству
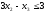 проходит через точки
проходит через точки
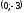 и
и
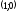
-
Строим на плоскости прямые, соответствующие данным прямым.
-
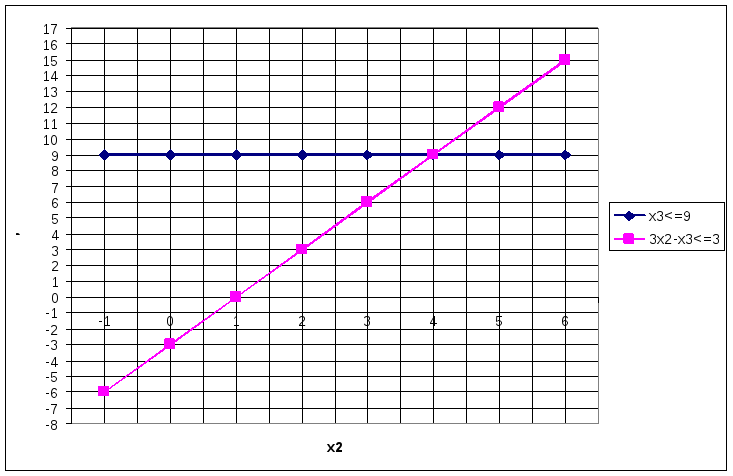
Определяем ОДЗ (Область допустимых значений) данной системы неравенств. ОДЗ- это многогранник, ограниченный заданной системой неравенств, каждая точка которого удовлетворяет всем неравенствам ( условиям).

Таким образом, ОДЗ, удовлетворяющая всем условиям следующая:
-
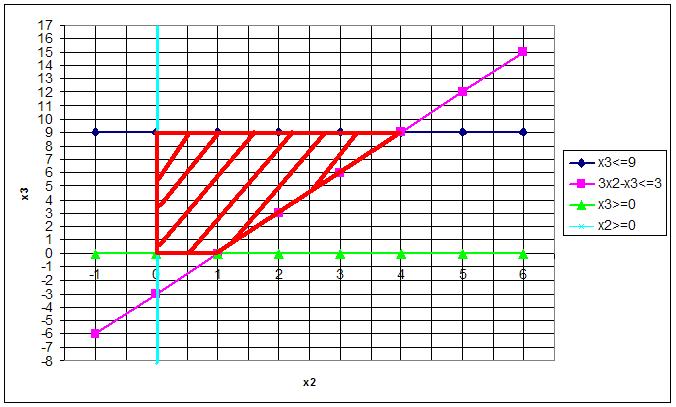
Строим вектор целевой функции
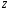 .
Для этого необходимо построить линию
уровня целевой функции, где
.
Для этого необходимо построить линию
уровня целевой функции, где
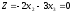 ,
а затем определить в какую сторону
целевая функция возрастает.
,
а затем определить в какую сторону
целевая функция возрастает.
Линия уровня целевой функции
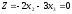 проходит через точки
проходит через точки
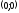 и
и
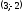 .
.
Чтобы определить градиент возрастания
целевой функции можно взять две точки
выше и ниже линии уровня целевой функции
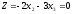 ,
подставить данные значения в уравнение
целевой функции
,
подставить данные значения в уравнение
целевой функции
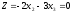 и посмотреть, в какой точке значение
и посмотреть, в какой точке значение
 больше нуля.
больше нуля.
В нашем случае можно взять две точки:
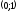 и
и
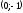 :
:


Таким образом, целевая функция возрастает вниз (см. рисунок), а вверх соответственно убывает.
-
Мысленно передвигая параллельно линию уровня целевой функции вверх, нужно определить крайнюю точку ОДЗ, которую пересекают линии уровня целевой функции.
Для данной ОДЗ целевая функция
 достигает минимума в точке С, а максимума
в точке A.
достигает минимума в точке С, а максимума
в точке A.
Определим координаты точек A и С.
Координаты точки A можно
определить из графика:
 .
Тогда, подставив координаты точки А в
.
Тогда, подставив координаты точки А в
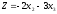 ,
получаем значение максимума целевой
функции для заданной системы неравенств:
,
получаем значение максимума целевой
функции для заданной системы неравенств:
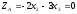
Точка С образована пересечением двух прямых
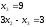
Решив данную систему уравнений, получаем
координаты точки С
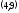 .
Подставив координаты точки С в
.
Подставив координаты точки С в
 ,
получаем значение максимума целевой
функции для заданной системы неравенств:
,
получаем значение максимума целевой
функции для заданной системы неравенств:

Ответ:
 ,
,

-
Решение задач Линейного программирования симплекс-методом
Симплекс-метод был разработан и впервые применен для решения задач в 1947 г. американским математиком Дж. Данцигом. Симплексный метод в отличие от геометрического универсален. С его помощью можно решить любую задачу линейного программирования. В основу симплексного метода положена идея последовательного улучшения получаемого решения.
Геометрический смысл симплексного метода состоит в последовательном переходе от одной вершины многогранника ограничений к соседней, в которой целевая функция принимает лучшее (или, по крайней мере, не худшее) значение до тех пор, пока не будет найдено оптимальное решение - вершина, где достигается оптимальное значение функции цели (если задача имеет конечный оптимум).
Таким образом, имея систему ограничений, приведенную к канонической форме (все функциональные ограничения имеют вид равенств), находят любое базисное решение этой системы, заботясь только о том, чтобы найти его как можно проще. Если первое же найденное базисное решение оказалось допустимым, то проверяют его на оптимальность. Если оно не оптимально, то осуществляется переход к другому, обязательно допустимому базисному решению. Симплексный метод гарантирует, что при этом новом решении целевая функция, если и не достигнет оптимума, то приблизится к нему (или, по крайней мере, не удалится от него). С новым допустимым базисным решением поступают так же, пока не отыщется решение, которое является оптимальным.
Процесс применения симплексного метода предполагает реализацию трех его основных элементов:
1) способ определения какого-либо первоначального допустимого базисного решения задачи;
2) правило перехода к лучшему (точнее, не худшему) решению;
3) критерий проверки оптимальности найденного решения.
Симплексный метод включает в себя ряд этапов и может быть сформулирован в виде четкого алгоритма (четкого предписания о выполнении последовательных операций). Это позволяет успешно программировать и реализовывать его на ЭВМ. Задачи с небольшим числом переменных и ограничений могут быть решены симплексным методом вручную.
