Міністерство освіти і науки України

Криворізький коледж Національного авіаційного університету

Опір матеріалів

Методичні вказівки

до виконання самостійної роботи курсантів

спеціальності 6.070103 «Обслуговування повітряних суден»

Частина І.

Кривий Ріг

2008

Методичні вказівки складено відповідно до програми курсу «Опір матеріалів» спеціальності 6.070103 «Обслуговування повітряних суден». Методичні вказівки містять основні теоретичні положення, запитання для самоперевірки, приклади ваконання завдання, завдання для самостійного виконання,а також список рекомендуємої літератури.

Затверджено на засіданні циклової комісії «Фундаментальних та професійно – орієнтованих дисциплін»

Протокол № 2 від 19.11. 2008р.

Укладач : Войтенко Н.В.

Рецензент : Войтенко В.А.

ВСТУП

Розв’язання переважної більшості задач опору матеріалів потребує визначення небезпечних, найбільш навантажених перерізів стрижнів, що входять до складу різноманітних конструкцій. Для визначення таких перерізів будують епюри внутрішніх силових факторів, тобто графічне зображення характеру їх змін за довжиною стрижня.

Найбільш складна побудова епюр в разі дії на стрижень поперечних навантажень у випадку розрахунку балок або рам.

Оскільки рама містить в собі декілька стрижнів, що жорстко скріплені один з одним, засвоювання прийомів побудови епюр слід починати саме з балок, тобто окремих стрижнів, на які діють поперечні навантаження. Набутий при цьому досвід значно полегшує сприйняття прийомів побудови епюр для рам.

Метою цих методичних вказівок є створення допоміжного матеріалу, який би комплексно та в подробицях освітлював процедуру побудови епюр для балок і нагадував студентам, особливо заочної форми навчання, про можливість самостійного засвоювання даного розділу. Саме такій меті і підпорядкований зміст цих вказівок. Вони містять необхідний теоретичний матеріал, ряд детально розібраних прикладів, завдання для самостійного розв’язування, відповіді до цих завдань, за допомогою яких студент зможе проконтролювати себе і виявити зроблені ним помилки.

Розділ 1. Геометричні характеристики перерізів. Основні теоретичні відомості.

Міцність і жорсткість бруса при заданих матеріалі і довжині залежать від розмірів і форми перерізу. Для кількісної оцінки цієї залежності служать геометричні характеристики перерізів.

У випадку розтягу і стисканні характеристикою перерізу, незалежно від його форми є площа, але при згині, крученні, складних деформаціях цієї характеристики недостатньо. Тому до інших геометричних характеристик перерізів, які використовуються при згині, крученні та складних деформаціях належать статичні моменти, моменти інерції, радіус інерції та момент опору.

В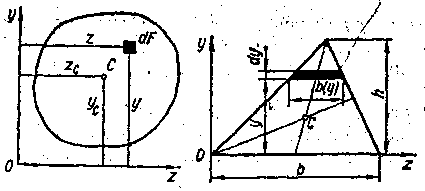міння визначати необхідні геометричні характеристики є необхідним для розрахунків брусів на міцність та жорсткість при різних видах деформацій.

Р

Рис 1.

озглянемо довільну фігуру (поперечний переріз), зв’язаний з координатними осями Оz та Оу (рис 1). Виділимо елемент площі dF з координатами z, у. за аналогією з виразом для моменту сили відносно якої – небудь осі можна записати вираз і для момету площі, який називається статичним моментом. Так, добуток елемента площі dF на відстані у від осі Оz називається статичним моментом елемента площі відносно осі Оz. Аналогічно - статичний момент елемента площі відносно осі Оу. Підсумувавши такі добутки по всій площі F фігури, дістанемо відповідно статичні моменти відносно осей z та у.

(1.1)

Статичний момент виражається в одиницях довжини в третьому степені (наприклад, см³).

Позначимо z_c, y_c координати центра ваги фігури: Продов­жуючи аналогію з моментами сил, на підставі теореми про момент рівнодійної можна записати такі вирази:

(1.2)

д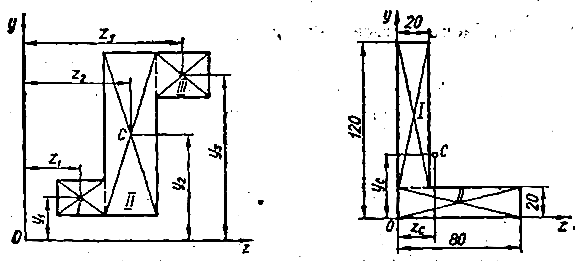е F – площа фігури;

Звідси координати центра ваги

(1.3)

Із формул (1.2) випливає, що статичні моменти площі відносно цент­ральних осей, тобто осей, що проходять через центр ваги, дорівнюють нулю.

Д

Рис 2

ля визначення статичних моментів складної фігури її розбивають на прості частини (рис. 2), для кожної з яких відомі площа F та по­ложення центра ваги z_i і у_i. Статичний момент площі всієї фігури від­носно даної осі визначається як сума статичних моментів кожної частини:

(1.4))

За формулами (1.3) та (1.4) легко знайти координати центра ваги складної фігури:

(1.5)

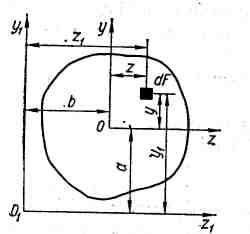
Осьовим, або екваторіальним, моментом інерції площі фігури нази­вають інтеграл добутків площ елементарних площадок на квадрати відстаней їх від розглядуваної осі, що лежить у площині фігури. Так, моменти інерції довільної фігури (рис. 3) відносно осей z та у відпо­відно

(1.6)

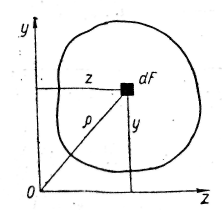
Полярним моментом інерції площі фігури відносно даної точки (полюса O) називають інтеграл добутків площ елементарних площадок на квадрати відстаней їх від полюса (рис. 3):

(1.7)

Якщо через полюс проведено систему прямокутних осей z та у, то ² = z² + у². Тоді з виразу (1.7) маємо

(1.8)

Рис 3.

Осьові та полярні моменти інерції можуть набирати лише додатних значень.

Відцентровим моментом інерції називають інтеграл добутків площ елементарних площадок на відстані їх від осей z та у.

(1.9)

Відцентровий момент інерції залежно від положення осей може бути додатним чи від'ємним або дорівнювати, нулю. Так, відцентровий мо­мент інерції площі фігури, яку показано на рис. 4, а, відносно осей z та у додатний, бо координати z, у всіх елементів площі додатні. При повороті осей навколо початку координат на 90° (рис. 4, б) знак від­центрового моменту інерції фігури змінюється на протилежний, бо в цьому положенні координати z всіх елементів додатні, а координати у від'ємні.

Очевидно, при поступовому повороті осей мож­на знайти таке положення їх, при якому відцент­ровий момент інерції дорівнюватиме нулю. Такі осі називають головними осями інерції. Дві взаєм­но перпендикулярні осі, з яких хоча б одна є віс­сю симетрії фігури, завжди будуть її головними осями інерції, оскільки в цьому разі кожній до­датній величині zydF відповідає така сама від'ємна по інший бік від осі симетрії (рис. 4, в) і сума їх по всій площі фігури дорівнює нулю.

Рис 4.

Головні осі, що проходять через центр ваги перерізу, називають головними центральними осями.

Момент інерції площі фігури виражається в одиницях довжини в четвертому степені (наприклад, см⁴).

При розв’язанні різних практичних задач часто виникає потреба визначити моменти інерції складних перерізів тих чи інших осей, що лежать у площині фігури. Для стандартних перерізів – кутових рівнобоких (рис 5,а) та нерівнобоких (рис 5, б), двотаврових (рис 5, в), швелерних (рис5, г) та інших – моменти інерції відносно різних осей наведено в таблицях сортаментів (додаток) поряд з розмірами, площами перерізів, положенням центрів ваги та іншими характеристиками.

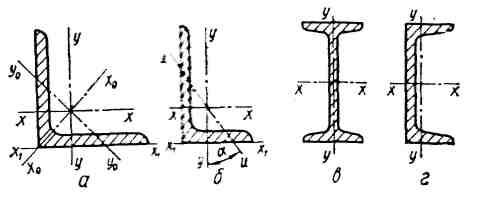
Рис 5.

При визначенні моментів інерції складних перерізів їх можна розбити на прості частини, моменти інерції яких відомі.

Якщо моменти інерції J_z, J_y, J_zy відносно центральних осей z, y відомі, то моменти інерції відносно осей, паралельних центральним (рис 6), визначають за формулами:

Рис 6

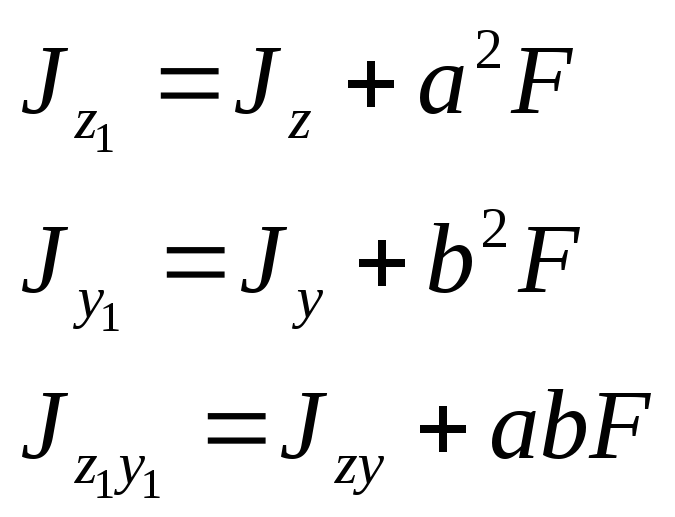(1.10)

Координати a, b у формули треба підставляти, враховуючи іхній знак.

Я кщо відомі моменти інерції J_z, J_y, J_zy відносно центральних осей z, y, то визначити моменти інерції відносно осей, які повернуто на кут  проти годинникової стрілки, вважаючи кут повороту у цьому напрямі додатним (рис 7), можна за формулами:

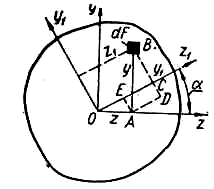
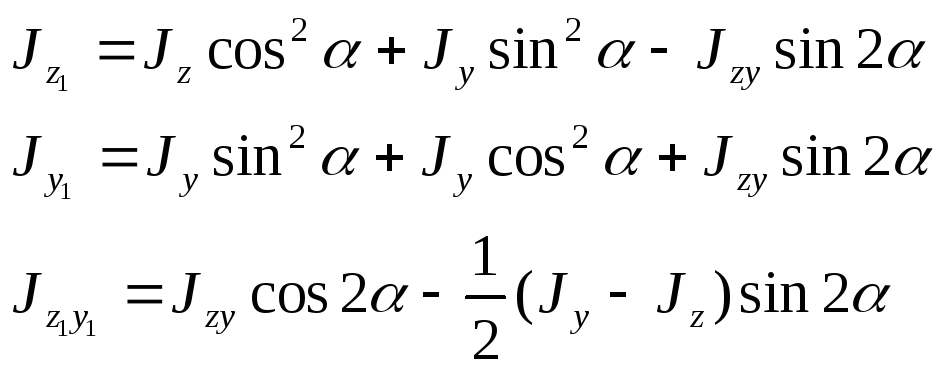(1.11)

Найбільш практичне значення мають головні ц

Рис 7

ентральні осі,відцентровий момент інерції відносно яких дорівню\ нулю. Осьові моменти інерції відносно цих осей набувають екстремальних значень.

Кут ₀, що визначає положення головних осей, обчислюється за формулою:

(1.12)

Добуті двоє значень кута  різняться між собою на 90⁰ і дають положення головних осей. Менший із цих кутів за модулем не перевищує /4 (45⁰).

Моменти інерції відносно головних осей називаються головними моментами інерції і обчислюються за формулою:

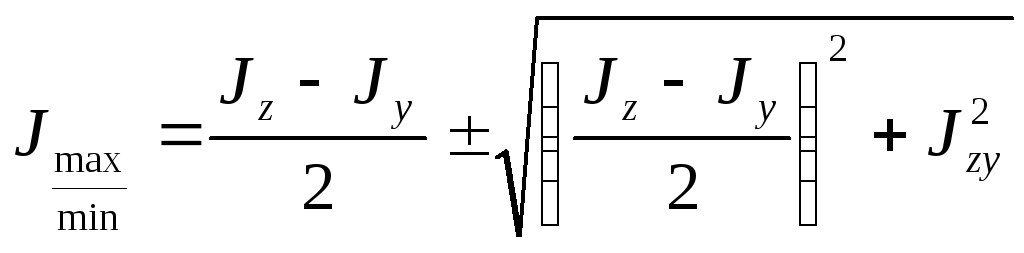(1.13)