3. Вопросы для самопроверки.

1. _{Дайте определение первообразной функции неопределённого интеграла. Приведите примеры.}

2. _{Сформулировать свойства неопределённого интеграла.}

3. _{В чём заключается геометрический смысл неопределённого интеграла?}

4. _{Назовите основные методы интегрирования.}

5. _{Решите: 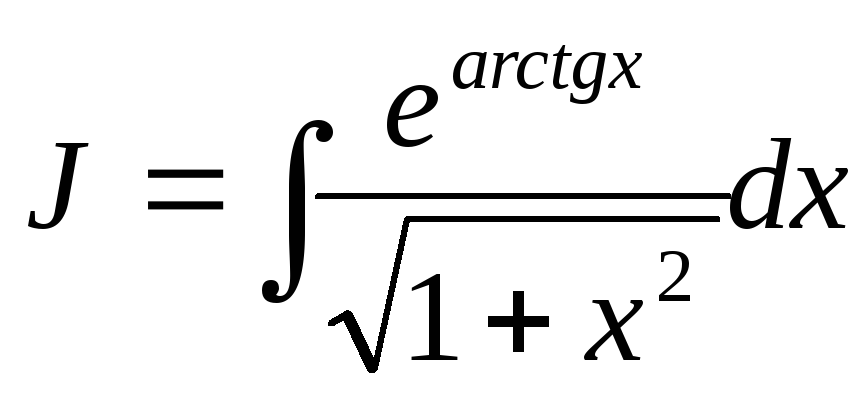методом подстановки.}

6. _{Примените формулу интегрирования по частям к интегралу:}

7. _{Объяснить, почему ∫x}²_{cos x}³_{dx решается способом подведения функции под знак дифференциала. Можно ли решить этот интеграл методом подстановки?}

Тема 8. Определённый интеграл по отрезку.

_{Определение: Определённым интегралом по отрезку a;b от функции f (x) называется предел интегральной суммы , если этот предел существует и не зависит ни от деления отрезка a;b на части, ни от выбора точек  внутри каждой из частей при условии, что длина наибольшего из частичных отрезков (∆xi) стремится к нулю, т.е}

_{Числа a,b называются соответственно нижним и верхним пределами интегрирования, т.е a;b-отрезок интегрирования.}

Свойства определённого интеграла по a;b.

_1.

_2.

_3.

_4.

_{5. С- постоянная}

Правила вычисления определённого интеграла по a;b

1

_{функция для f(x),}

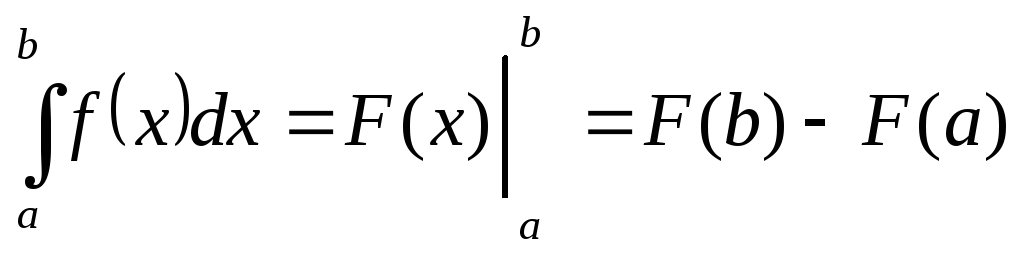. _{- формула Ньютона-Лейбница, где F(x)- первообразная}

2. _{- интегрирование по частям.}

3. _{, где x=(t) функция непрерывная вместе со своей производной}

_{на ;}

_{Например: Найти значение определённого интеграла}

Решение:

Решаем методом подстановки

x	1	e
t	0	1

Положим

Тогда

2. Несобственные интегралы.

К несобственным интегралам относятся:

1. Интегралы с бесконечными пределами интегрирования вида:

2. _{Интегралы от разрывных функций (от неограниченных функций).}

Пример 1. _{- несобственный интеграл 2) типа, т.к на отрезке -2;9 функция терпит бесконечный разрыв в точке x=0.}

_{Пример 2. Вычислить}

_{Решение}

_{Пример 3. Вычислить}

_{Решение:}

_{Т.к - чётная функция.}

_Тогда

_{Замечание. Если предел несобственного интеграла существует и конечен, то несобственный интеграл называется сходящимся.}

_{Если же предел не существует или равен бесконечности, то интеграл называется расходящимся.}

2. Приложения определённого интеграла по a;b

1. _{-площадь криволинейной трапеции, где y=f (x)- кривая, ограничивающая криволинейную трапецию, aABb- криволинейная трапеция.}

2. 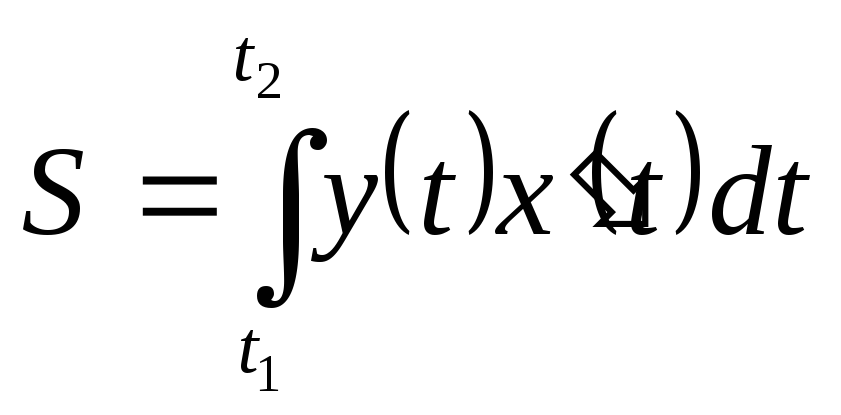_{- площадь криволинейной трапеции, если кривая задана}

_{параметрически:}

_{3. - площадь криволинейного сектора, ограниченного кривой, заданной в полярных координатах, где r = r(a) - уравнение кривой.}

4. _{вычисление длины дуги кривой y=f(x) на a;b}

_{5. Вычисления объёма тела вращения.}

Е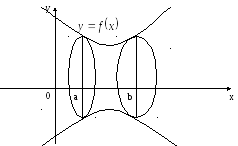сли криволинейная трапеция вращается вокруг оси OX, то объём тела вращения вычисляется по формуле:

6. Статические моменты и моменты инерции дуги плоской кривой y=f(x), (a  x  b) вычисляются по формулам (соответственно):

где - дифференциал дуги кривой y=f(x)

7. Координаты центра тяжести однородной дуги плоской кривой y=f(x) (a  x  b)

выражаются формулами:

_{где L-длина дуги.}