2.1 Операции над нечеткими множествами
Над нечеткими множествами можно производить различные операции, при этом необходимо определить их так, чтобы в частном случае, когда множество является четким, операции переходили в обычные операции теории множеств, то есть операции над нечеткими множествами должны обобщать соответствующие операции над обычными множествами. При этом обобщение может быть реализовано различными способами, из-за чего какой-либо операции над обычными множествами может соответствовать несколько операций в теории нечетких множеств.
Для определения пересечения и объединения нечетких множеств наибольшей популярностью пользуются следующие три группы операций:
-
Максиминные:
-
Алгебраические:
-
Ограниченные:
Дополнение
нечеткого множества во всех трех случаях
определяется одинаково:
Пример. Пусть A — нечеткое множество "от 5 до 8" (рис.1.3а) и B — нечеткое множество "около 4" (рис.1.3б), заданные своими функциями принадлежности:
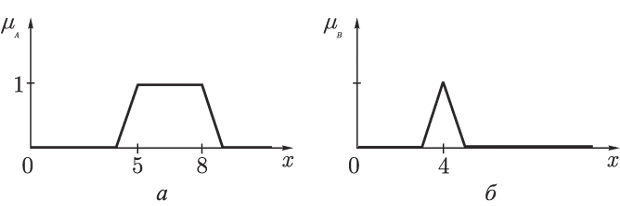
Рис. 1.3.
Тогда, используя максиминные операции, мы получим множества, изображенные на рис.1.4.
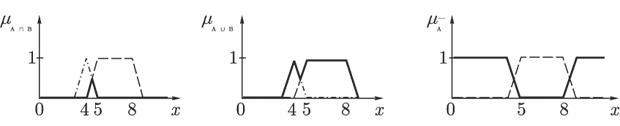
Рис. 1.4.
Заметим,
что при максиминном и алгебраическом
определении операций не будут выполняться
законы противоречия и исключения
третьего 
,
а в случае ограниченных операций не
будут выполняться свойства
идемпотентности 
и
дистрибутивности:
Можно показать, что при любом построении операций объединения и пересечения в теории нечетких множеств приходится отбрасывать либо законы противоречия и исключения третьего, либо законы идемпотентности и дистрибутивности.
Носителем нечеткого
множества A называется
четкое множество A таких
точек в U,
для которых величина 
положительна,
т.е.
Высотой нечеткого
множества A называется
величина 
Нечеткое
множество A называется нормальным,
если 
.
В противном случае оно называется субнормальным.
Нечеткое
множество называется пустым,
если
.
Очевидно, что в данном универсуме U существует
единственное пустое нечеткое множество.
Непустое субнормальное нечеткое
множество можно привести к нормальному
(нормализовать) по формуле:
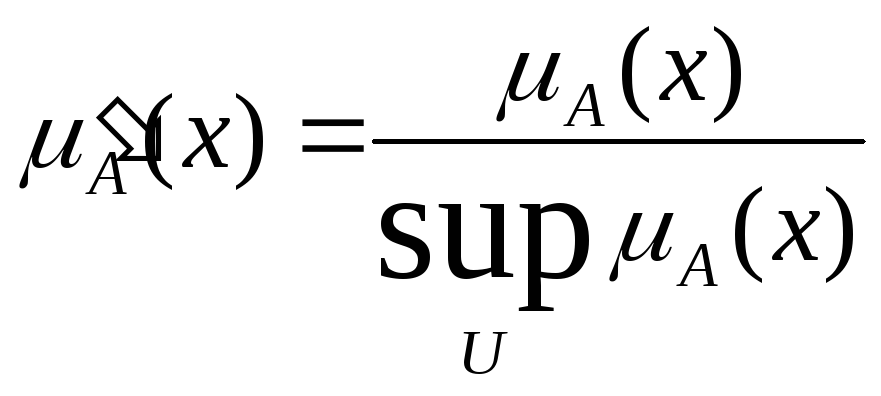
Заключение в этой работе были рассмотрены:
1) определение бинарных отношений и способы их задания в виде:
-Подмножества декартова произведения
-графа
-матрицы отношений
2) Операции над отношениями:
-пересечение
-объединение
-дополнение
-построение обратного отношения
-произведение отношений
-транзитивное замыкание
И графический и матричный способ выполнения этих операций.
3) такие свойства отношений как:
-рефлексивность
-симметричность
-транзитивность
Например рефлексивным является отношение «быть одногруппником» оно же симметрично и транзитивно;
Не симметричным будет отношение «быть руководителем»
Не транзитивным- отношение перпендикулярности на множестве прямых плоскости
4) относительно каких операций отношения сохраняют свои свойства. Например:
Объединение, пересечение, произведение отношений, обратное отношение и транзитивное замыкание сохраняют рефлексивность.
Такие операции как пересечение, обратное отношение и транзитивное замыкание сохраняют транзитивность.
5) отношения эквивалентности. Бинарное отношение α называется отношением эквивалентности на X, если α рефлексивно, симметрично и транзитивно. Например:
-отношение подобия на множестве фигур плоскости
-отношение сравнимости по модулю m
-«быть однокурсником»
Если на множестве М задано отношение эквивалентности то оно разбивает это множество на классы эквивалентности (верно и обратное утверждение); классы эквивалентности:
- не пусты
-не пересекаются
-в объединении дают всё множество М
Например в детской игре если игрушки распределить по цвету, то будет произведено разбиение множества игрушек на классы по отношению «иметь один цвет»
Отношение эквивалентности лежит в основе всевозможных классификаций;
Например иерархической:
При иерархической классификации все множество разлагается на классы эквивалентности, после чего каждый класс разлагается на классы эквивалентности по другому отношению и т. д. Такая классификация применяется, например, в биологии (царства живых существ, типы, классы, отряды, роды, виды). В математике иерархическая классификация используется, например, при классификации линий второго порядка.
6) основные понятия связанные с нечеткими множествами
Например: Нечеткое множество, функция принадлежности, степень принадлежности и прочие.
7) такие операции над нечеткими множествами как пересечение и объединение.