1.2 Операции над отношениями
Так как бинарные отношения являются множествами, то к ним применимы все понятия, которые вводятся для множеств: понятие равенства, включения, а также операции пересечения, объединения и дополнения. В этом разделе мы будем считать, что все отношения заданы на одном и том же множестве X.
Пусть α и β -
два бинарных отношения на множестве X.
Каждому из них соответствует некоторое
множество пар (подмножества 
и
).
Определение 2.1. Пересечением отношений
α
и β, заданных
на множестве X, называется
отношение 
такое,
что:
Пример 2.1. Пересечением отношений "не меньше" и "не равно", определенных на множестве действительных чисел R, является отношение "строго больше":
.
Определение 2.2. Объединением отношений α и β заданных на множестве X, называется отношение , такое, что:
Примером является отношение "быть ребенком".
Определение 2.3. Разностью отношений α и β, заданных на множестве X, называется отношение α\β, такое, что:
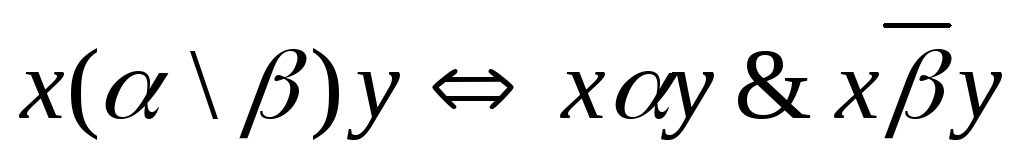
Пример 2.3. Разностью отношений "не меньше" и "не больше" на R является отношение "больше":
.
Пример 2.4. Разностью отношений "быть ребенком" и "быть дочерью", определенных на множестве всех людей, является отношение "быть сыном".
Определение 2.4. Дополнением 
отношения α,
определенного на множестве X,
называется отношение, определяемое
подмножеством пар из X
X,
не входящих в :
Пример 2.5.
Дополнением отношения "не меньше"
на R является
отношение "меньше":
Отметим, что приведенные выше определения являются просто перефразировками соответствующих определений для обычных множеств и все свойства теоретико-множественных операций пересечения, объединения и дополнения, имеющие место для произвольных множеств, выполняются и для отношений.
Кроме теоретико-множественных операций для отношений вводятся некоторые дополнительные операции, которые связаны с их специфической структурой. Мы рассмотрим две такие операции.
Определение 2.5. Если в каждой упорядоченной паре, принадлежащей отношению α, поменять местами первую и вторую компоненты, то получим новое отношение, которое называется обратным для отношения α и обозначается через α-1:
.
Пример 2.6. Обратным для отношения "не меньше" на множестве действительных чисел R является отношение "меньше":
.
Пример 2.7. Обратным для отношения "быть родителем" на множестве людей является отношение "быть ребенком".
Граф отношения α-1 получается из графа отношения переориентацией всех дуг (рис. 4).
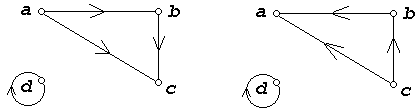
(а) Отношение α (б) Отношение α-1
Рис. 4. Графы отношений α и α-1
Если отношение задано с помощью булевой матрицы, то, поменяв в ней местами строки и столбцы, получим булеву матрицу отношения α-1 (рис 5).
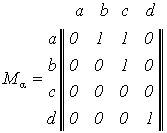
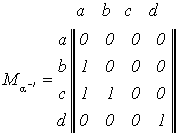
(а) Матрица отношения α (б) Матрица отношения α-1
Рис. 5. Матрицы отношений α и α-1
Определение 2.6. Произведением или композицией отношений α
и
β,
заданных на множестве X,
называется отношение α°β,
состоящее из таких кортежей (x, z),
для которых существует элемент 
,
удовлетворяющий условию 
и
:
Пример 2.8. Произведением отношений "быть братом" и "быть отцом" является отношение "быть братом одного из родителей", т. е. "быть дядей".
Если отношения α и β на некотором множестве X заданы с помощью графов, то принадлежность пары (x, z) к отношению α°β означает, что из вершины x в вершину z можно попасть точно за два шага, причем первый из них делается по дуге отношения α, а второй - по дуге отношения β.
На рисунке 6 изображены графы, представляющие отношения α (точечные дуги) и β(пунктирные дуги), и графы, представляющие произведения отношений α°β и β°α.
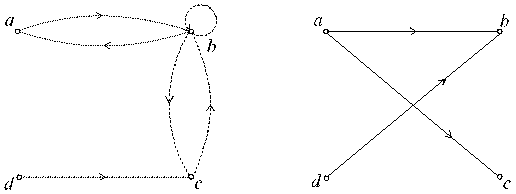
(а) Графы отношений α и β (б) Граф отношения α°β
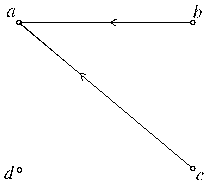
(в) Граф отношения β°α
Рис.
6.
Пример произведения отношений (α°β
β°α)
Пример, приведенный на рисунке 6, показывает, что для произведения отношений коммутативный закон не выполняется.
Для
выражения матрицы произведения двух
отношений α и β,
заданных булевыми матрицами 
и 
,
введем понятие "булево сложение"
,
определив его следующим образом:
, 
, 
,
.
Если
теперь M =(aij), M =(bjk), (i,j,k=1,2,…,n),
то
,
где cik = ai1 b1k 
…
ain bnk
Матрица 
называется булевым
произведением матриц
и 
.
Легко проверить, что
является
булевой матрицей произведения α°β.
Пример 2.9. Вычислим матрицы произведений α°β и β°α отношений α и β , представленных графами на рисунке 6.
Для
этого перемножим соответствующие
матрицы 
и 
(строки
и столбцы матриц упорядочены в соответствии
с алфавитным порядком букв a,
b, c, d,
обозначающих вершины графа).
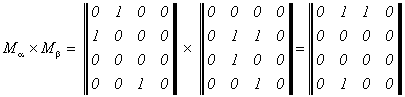
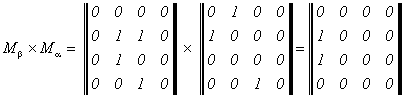
Определим еще одну унарную операцию над отношением.
Определение 2.7. Транзитивным
замыканием отношения α называется
бинарное отношение 
такое,
что
тогда и только тогда, когда существует
такая цепочка элементов из X:
z0 = x, z1, z2, ..., zn = y,
что между соседями в этой цепочке выполнено отношение α:
z0 az1, z1a z2, ..., zn-1 azn.
П
ример 2.10.
На рисунке
7
изображены графы, представляющие
отношение α
и его транзитивное замыкание 
.
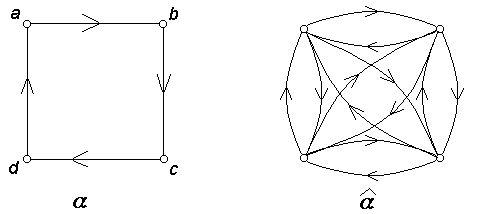
Рис.
7.
Транзитивное замыкание 
отношения α
В
матричной форме операция транзитивного
замыкания отношения α
выражается
через объединение степеней
матрицы 
отношения α:
В приведенной формуле объединение матриц понимается следующим образом:
.