
- •Глава 12 Двойной интеграл.
- •12.1. Понятие двойного интеграла.
- •12. 2. Геометрический смысл двойного интеграла.
- •12.3. Вычисление двойных интегралов в прямоугольных декартовых координатах.
- •12.4. Правила вычисления двойных интегралов и порядок приведения двойного интеграла к повторному.
- •Решение практических задач
- •Примеры для самостоятельного решения.
Решение практических задач
П р и м е р 1.
Вычислить
![]() ,
если S
ограничена линиями: у
= х,
,
если S
ограничена линиями: у
= х,
![]() ,
х =
4. Этот же интеграл вычислить, изменив
порядок интегрирования.
,
х =
4. Этот же интеграл вычислить, изменив
порядок интегрирования.
Р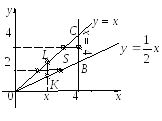 ешение.
Прежде всего, на чертеже надо представить
область S.
Определимся: внутреннее интегрирование
проводить по переменной у,
а внутреннее – по переменной х.
ешение.
Прежде всего, на чертеже надо представить
область S.
Определимся: внутреннее интегрирование
проводить по переменной у,
а внутреннее – по переменной х.
Найдем пределы интегрирования. Область S спроектируем на ось Ох. Получим отрезок [0, 4]. Этим определяются нижний и верхний пределы изменения переменной х во внешнем интеграле. Затем на оси Ох выберем произвольную точку х ∈ (0, 4), через ко-
торую проведена
прямая параллельная оси Оу
и на ней рассмотрен отрезок KL,
содержащийся в области S.
Точка К
является точкой входа в область S
и лежит на прямой
![]() точка L
является точкой выхода из области
S
и лежит на прямой у
= х.
точка L
является точкой выхода из области
S
и лежит на прямой у
= х.
Таким образом,
область S
ограничена снизу прямой
![]() ,
сверху прямой у
= х.
Следовательно, переменная у
изменяется в пределах
,
сверху прямой у
= х.
Следовательно, переменная у
изменяется в пределах
![]() .
.
Тогда получаем:
 .
.
Вычисление следует начинать с внутреннего интеграла

в котором величина х должна рассматриваться как постоянная.

Вычисляем теперь внешний интеграл.
![]()
Вычислим этот же двойной интеграл, изменив порядок интегрирования: внутреннее интегрирование будем производить по переменной х, а внешнее – по переменной у.
Из рисунка видно, что левая часть контура области S – одна линия у = х, а его правая часть состоит из двух линий ОВ и ВС определяемых разными уравнениями
(ОВ)
![]() ,
(ВС)
х
= 4.
,
(ВС)
х
= 4.
В этом случае область S следует разбить на части так, чтобы каждая из них справа ограничивалась тоже одной линией, иначе говоря, линией, определяемой одним аналитическим выражением. Такими частями будут S1 –∆OLB и S2 – ∆LВС. S1 + S2 = S.
Интеграл представляется как сумма интегралов
![]() .
.
Так как теперь внутренние интегралы будут вычисляться по переменной х, то уравнения линий, ограничивающих каждую из областей S1 и S2 должны быть решены относительно этой переменной S1 ограничена линиями: х = у, х = 2у, у = 2. Точка В имеет координаты (2; 4).
Область S2 ограничена линиями: у = 2, х = у, х = 4.
Спроектировав
каждую из областей интегрирования S1
и S2
на ось Оу
получим пределы внешних интегралов: в
первом интеграле у1
= 0 и из
 у2
= 2; во втором интеграле – у1
= 2 и из
у2
= 2; во втором интеграле – у1
= 2 и из
![]() у2
= 4. Выберем на отрезке [0; 2] произвольную
точку у
и проведем через нее прямую, параллельную
оси Ох.
у2
= 4. Выберем на отрезке [0; 2] произвольную
точку у
и проведем через нее прямую, параллельную
оси Ох.
Нетрудно видеть, что в области S1 переменная х изменяется от значения х1 = у на левой части контура (т. е. на OL), до ее значения х2 = 2∙у на его правой части (т. е. на ОВ).
Таким образом, при интегрировании области S1 во внутреннем интеграле пределами будут у и 2∙у. При вычислении внутреннего интеграла переменную у необходимо считать величиной постоянной:

![]()
При интегрировании области S2 во внешнем интеграле переменная у изменяется на отрезке [2; 4], т. е. от 2 до 4.
Определим, в каких пределах изменяется переменная х внутреннего интеграла. Для этого возьмем на интервале (2; 4) произвольную точку, проведем через нее прямую, параллельную оси Ох. Нетрудно видеть, что на левой части LC контура области S2 х имеет значение х1 = 4. Таким образом, в области S2 пределами внутреннего интеграла по переменной х будут у и 4.
![]()
Искомый интеграл равен сумме
![]()
Поскольку подынтегральная функция х3 + у3 непрерывна, то результаты вычислений, как и следовало ожидать, совпали: они не зависят от порядка интегрирования. Из этого примера видно, что выбор порядка интегрирования не безразличен. Выбрав рационально порядок интегрирования можно сократить вычисления.
П р и м е р 2. Вычислить объем тела z = 3x2 + y2; y = 2; х = 1; z = 0; у = 0; х = 0.
Решение. Найдем пределы интегрирования. Так как при z = 0 х = 0, значит 0 ≤ x ≤ 1. Тогда у изменяется от 0 до 2 (по условию задачи). Подставим найденные значения в формулу нахождения объема и получим:
![]()
![]()
