1. Коммутативность

x₁ & x₂ = x₂ & x_1.

x₁ v x₂ = x₂ v x_1.

2. Ассоциативность

x₁ v (x₂ v x₃) = (x₁ v x₂) v x_3.

x₁ & (x₂ & x₃) = (x₁ & x₂) & x_3.

3. Дистрибутивность

x₁ & (x₂ v x₃) = (x₁ & x₂) v ( x1 & x₃ ).

x₁ v (x₂ & x₃) = (x₁ v x₂) & ( x1 v x₃ ).

Отметим также важные соотношения:

X v X = X, X & X = X, X v 1 = 1, X & 1 = X,

X v 0 = X, X & 0 = 0, X v X = 1, X & X = 0.

Положим x ^ = { X , если  = 1; X , если  = 0 } .

Утверждение. Любая функция алгебры логики кроме 0 может быть представлена в форме

f(x ₁...x_n) =  x₁ ^ & x₂ ^... & x_n ^ (5.1)

При этом дизъюнкция в правой части берется только по тем наборам аргументов, на которых функция, заданная таблично, обращается в 1.

Определение. Представление функции алгебры логики в виде (5.1) называется ДСНФ - дизъюнктивной совершенной нормальной формой.

Для построения ДСНФ необходимо выполнить следующие шаги:

• выбрать в таблице истинности заданной функции все наборы аргументов, на которых функция равна 1;

• выписать соответствующие этим наборам конъюнкции, при этом, если аргумент x_i входит в данный набор как 1, то он записывается без изменений, если же как 0 , то берется ;

• все полученные конъюнкции объединяются под знаком дизъюнкции.

Утверждение. Любая функция алгебры логики кроме 1 может быть представлена в форме:

f ( x1, x2,...,xn ) = & (x₁ ^ v x₂ ^ v ... v x_n ^ ). ( 5. 2 )

Конъюнкция берется только по тем наборам , на которых функция

равна 0.

Определение. Представление функции алгебры логики в виде

формы (1. 2) называется СКНФ - совершенной конъюнктивной нормальной формой. Для ее получения используют следующие действия:

• выбрать в таблице истинности заданной функции все наборы аргументов, на которых функция равна 0;

• выписать дизъюнкции, соответствующие этим наборам аргументов , учитывая ;

• все полученные дизъюнкции соединить под знаком конъюнкции.

5.2. Булева алгебра. Функциональная полнота

Определение. Алгеброй над множеством логических функций с двумя бинарными операциями, обозначаемыми как логическое умножение & и логическое сложение v и одной унарной операцией ( отрицанием )

• называется булевой алгеброй. Будем обозначать ее символом _B.

Рассмотрим свойства булевой алгебры.

1. Замкнутость

для  A и B  _B

A v B  _B

A & B  _B

2. Коммутативность

A & B = B & A

A v B = B v A

3. Ассоциативность

A v ( B v C) = (A v B) v C

4. Дистрибутивность

A & ( B v C) = (A & B) v (A & C)

A v ( B & C) = (A v B) & (A v C)

5. Идемпотентность

A v A = A & A = A.

6. Булева алгебра содержит элементы 0,1 , такие что для всякого

элемента A  _B справедливо:

A v 0 = A, A v 1 = 1

A & 0 = 0, A & 1 = A.

7. Для каждого элемента A  _B существует элемент , такой что

A v =1

A & =0.

8. Закон поглощения

A & (A v B) = A v A & B = A.

9. Закон Де Моргана

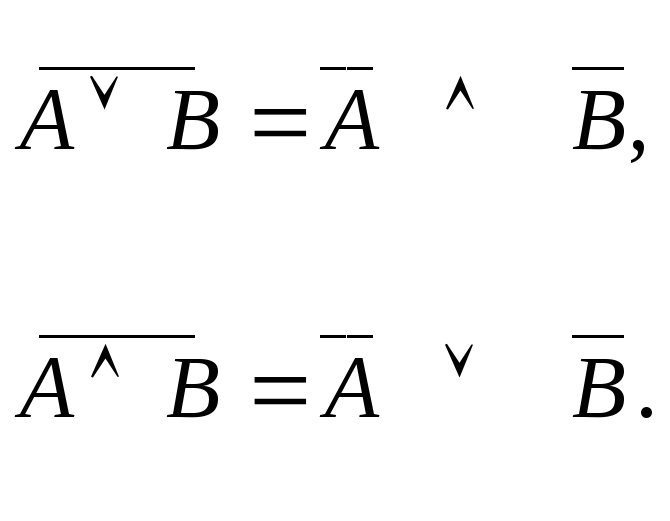
Определение. Система функций f₁, f₂... f_n  _B называется полной, если любая функция  из _B представима в виде суперпозиции функций f₁, f₂... f_n.

Определение. Система функций f₁, f₂... f_n  _B , являющаяся полной, называется базисом.

Определение. Минимальным базисом называется базис, для которого удаление хотя бы одной из функций f_i превращает систему функций в неполную.

Можно показать, что системы функций { &, } и { , } - полные. Система функций { &, , } является полной, но избыточной, так как она сохраняет свойства полноты и при удалении из нее & или . За не избыточность системы функций { &, } и { , } приходится платить избыточностью формул ( повышением сложности функций).

Определение. Алгебра над множеством логических функций с двумя бинарными операциями & и  называется алгеброй Жегалкина.