Обратной задачах эллипсометрии

В так называемой классической (традиционной) эллипсометрии, которую мы изучаем, измеряют в опыте два эллипсометрических параметра  и Δ для отражающей поверхности изучаемого объекта:

 = arctg(R_pp/R_ss) (9.1)

Δ = δ_p – δ_s (9.2)

где R_pp и R_ss, δ_p и δ_s – модули и фазы комплексных амплитудных коэффици-ентов отражения R^*_pp и R^*_ss линейно поляризованных р- и s-компонент плос-кого потока света, отражаемого объектом.

Их измерение само по себе ещё не решает задачи определения оптических и технологических свойств объекта, в частности, оптических свойств матери-ала отражающей повверхности. И возникает вполне естественно довольно важная (можно сказать, фундаментальная) проблема установления адекват-ного соответствия между измеряемыми в опыте эллипсометрическими пара-метрами  и Δ отражателя и оптическими параметрами вещественной среды изучаемого объекта. А последние описываются феноменологически в рамках классической электродинамики Максвелла-Лоренца главными комплексны-ми показателями преломления n^*_qv(ν), задаваемыми их действительной n_qv(ν) и мнимой k_qv(ν) частями как функций частоты  света:

n^*_qv(ν) = n_qv(ν) + ik_qv(ν) (9.3)

а также линейными (отнесёнными к длине пути d потока света) коэффициен-тами поглощения К_qv(ν) (в единицах см^–1):

К_qv(ν) = (2πν/с)dk_qv(ν) (9.4)

или, используя длину волны света: К_qv() = (2π/)dk_qv() (9.5)

которые описывают эффект ослабления амплитуды электрического (как обы-чно) поля Е_qv(ν) или E_qv() для бегущего вдоль главного q-направления в пространстве поглощающей среды плоского потока электомагнитных волн с собственной поляризацией v-типа. Напомним при этом, что в эллипсометрии имеют дело обычно с линейными поляризациями р– и s-типа для оптически неактивных отражателей, тогда как в поляриметрии оптически активных сред имеют дело с главными левой (ℓ) и правой (r)) круговыми поляризациями. Но мы ограничимся рассмотрением только оптически неактивных отражателей и отражением плоских потоков света с линейными р- и s-поляризациями.

Интерпретация результатов измерений эллипсометрических углов  и Δ для отражателя строится на основе корреляций этих углов с оптическими параметрами, т. е. с комплексными показателями преломления и толщинами слоёв на поверхности отражателя. Такие корреляции находят на основе реше-ния задачи о взаимодействии падающего на отражатель плоского потока све-та последовательным применением замкнутой системы уравнений Макс-велла-Лоренца для каждой области рассматриваемого отражателя.

Этой фундаментальной проблеме корреляции эллипсометрических углов  и Δ со свойствами и структурой отражающей оптической системы посвя-щено много научных работ, начиная от исторически исходных исследований Френеля и включая решение первой собственно эллипсометрической задачи, данное Друде, причём к таким работам относят и следующие общие работы: Борн М., Вольф Э. «Основы оптики»; Ландау Л.Д., Лифшиц Е.М. «Электродинамика сплошных сред»;: Аззам Р., Башара Н. «Эллипсометрия и поляризованный свет»; Основы эллипсометрии, под редакцией Ржанова А.В. (Новосибирск, 1980); Лоренц Г.А. «Теория электронов и её применения к явлениям света и теплового излучения»; Heavens C.S. “Optical properties of thin solid films”; Vasicek A. “Optics of thin films”; Беннет Х.Б., Беннет Д.М. «Прецизионные измерения в оптике тонких плёнок» / в книге «Физика тонких плёнок» (М., 1970, т.4).

Конечно, нет нужды обсуждать все эти известные работы, но следует использовать полученными в них результаты, относящиеся к анализу хотя и частных, по сути своей, задач, но весьма важных для понимания физики взаимодействия поляризованного излучения с тонкослойными системами и нашедшими, по понятной причине, широкие применения в эллипсометрии.

Во-первых, это рассмотренная ещё Друде задача об отражении поляризо-ванного света планарной системой в виде тонкой изотропной (прозрачной или поглощающей) плёнки на оптически изотропной подложке на границе с внешней средой, скажем, вакуумом или воздухом. Данное Друде решение задачи представляет комплексные амплитудные коэффициенты отражения R^*_p и R^*_s для линейных р- и s-поляризованных потоков света на отражателе:

R^*_p,s = [r^*_01p,s + r^*_12p,sexp(iβ₁)]/ [1 + r^*_01p,sr^*_12p,sexp(iβ₁] (9.5)

Здесь в свою очередь комплексные амплитудные коэффициенты отраже-ния r^*_01p,s и r^*_12p,s плоского потока света на границе раздела однородных оптически изотропных сред (0 и 1) и соответственно (1 и 2) определяются формулами Френеля:

r^*_ikp = (n^*_kcosθ_i – n^*_icosθ_k)/(n^*_kcosθ_i + n^*_icosθ_k) (9.6)

r^*_iks = (n^*_icosθ_i – n^*_kcosθ_k)/(n^*_kcosθ_i + n^*_kcosθ_k) (9.7)

где θ_i и θ_k – углы между направлениями бега пучков света по разные стороны (i, k) границы раздела сред (i и k) и нормалью к поверхности этих сред; а фазовое запаздывание β₁ световых волн в результате прохождения в оптической среде 1:

β₁ = (4πd₁n^*₁cosθ₁/) (9.8)

. Используя соотношения (9.5) для комплексных амплитудных коэффи-циентов отражения R^*_p и R^*_s для линейных р- и s-поляризованных компонент отражаемого объектом потока света и подставляя их в основное уравнение эллипсометрии ^*_ps в виде относительного амплитудного коэффициента отра-жения для линейно поляризованных р- и s- компонент, получим основное уравнение эллипсометрии для такой наипростейшей тонкослойной системы:

^*_ps = (R^*_p/R^*_s) = {[r^*_01p + r^*_12pexp(iβ₁)]/[1 + r^*_01pr^*_12pexp(iβ₁)]}/

/{[r^*_01s + r^*_12sexp(iβ₁)]/[1 + r^*_01sr^*_12sexp(iβ₁)]} (9.9)

Это соотношение (9.9) можно представить и так:

^*_ps = (tg)exp(iΔ) = ^*_ps(n^*_o, n^*₁, n^*₂; d₁,cosθ₁;) (9.10)

Oно (9.10) в свою очередь приводится к двум действительным уравне-ниям, которые определяют эллипсометрические паы  и Δ для отражателя:

 = arc tg(R^*_p/R^*_s) = arc tg^*_ps(n^*_o, n^*₁, n^*₂; d₁,cosθ₁;) (9.11)

Δ = arg [(R^*_p/R^*_s)] = arg [^*_ps(n^*_o, n^*₁, n^*₂; d₁,cosθ₁;)] (9.12)

где ^*_ps и arg ^*_ps = Δ = (δ_p – δ_s) – модуль и аргумент (фаза) относительного амплитудного коэффициента отражения ^*_ps для линейных р- и s-поляризо-ванных компонент отражаемого потока света.

Функциональные зависимости для эллипсометрических углов  и Δ для отражающей поверхности объекта на основе соотношений (9.11) и (9.12) даже для наипростейшей тонкослойной системыы, изученной ещё Друде, от параметров этой системы (от комплексных показателей внешней среды n^*_o, тонкослойной плёнки n^*₁, подложки n^*₂, толщины d₁ плёнки, угла падения θ_о, частоты ν света) оказываются усложнёнными и громоздкими. Oни могут анализироваться только при использовании численных расчётов, которые можно провести лишь с помощью высокопроизводительных ЭВМ. Сущест-вуют полученные на основе таких численных расчётов справочные издания, например, «Ellipsometric Tables of the Si – SiO₂ Systems for Mercury and He-Ne=Laser Spectral Lines» (Budapest, 1971). В нём, в частности, приведены так называемые эллипсометрические таблицы и кривые, показывающие в случае плёнки окиси кремния SiO₂ на кремниевой подложке Si в вакууме зависимо-сти эллипсометрических углов  и Δ от двух параметров плёнки: толщины d₁ и показателя преломления n₁ (когда мнимая часть k₁ = 0!) – для некоторых спектральных линий испускания ртути Hg и гелий-неонового (He-Ne) лазера. Такого рода расчёты даны также в книге авторского коллектива из Института полупроводников СО РАН в г. Новосибирске, а именно: Бурыкин И.Г., Во-робьёва Л.П., Грущецкий В.В. др. «Алгоритмы и программы для численного решения некоторых задач эллипсометрии», под редацией Ржанова А.В. (Новосибирск, Наука, 1980). Такого рода расчёты представляют собой так называемую прямую задачу эллипсометрии.

Результаты численных расчётов можно представлять и обычно представ-ляли (до персональных компьютеров) в виде зависимости эллипсометриче-ского угла Δ = Δ() от угла  в декартовых координатах (Δ, ), а толщина плёнки d₁ служила переменным параметром при заданном угле падения θ_о

Зависимости Δ = Δ(), рассчитанные для различных значений показателя преломления n₁ прозрачной плёнки при фиксированных угле падения θ_о света на плёнку и его длине волны  для рассмотренной тонкослойной системы (внешняя среда – плёнка – подложка) называют номограммой (рис.9-1).

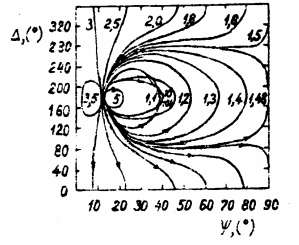рис.9-1

Здесь номограмма дана для тонкослойной системы воздух – прозрачная плёнка оксида германия GeO₂ – германиевая подложка Ge (рис. 9-1) при угле падения света θ_о = 70° и длине волны света  = 546,1 нм по работе Archer R.J. (JOSA – 1962, vol.110, N 2, p.354).

Построение номограммы Δ = Δ() есть решение прямой задачи эллипсо-метрии. Она сравнительно просто решается численным образом и легко программируется для конкретно рассмотренной не слишком усложнённой слоистой (планарной) системы с данными оптическими параметрами в виде действительных n_j и мнимых k_j частей комплексного показателя преломления n*_j и толщинами d_j соответственных j-х тонких слоёв системы.Численное решение прямой задачи эллипсометрии выполняют на цифровых ЭВМ.

А как решается прямая задача эллипсометрии для более усложнённых планарных систем, когда, например, имеется не одна плёнка, а, скажем, две или более тонких плёнок на подложке?

Решение прямой задачи эллипсометрии в случае многослойных систем не испытывает принципиальных затруднений благодаря использованию отрабо-танного изящного матричного метода. Этот метод основан на использовании четырёхкомпонентной (2х2) матрицы S, которая связывает компоненты элек-трического поля Е(z) световой волны на входе (i) и выходе (е) планарного тонкослойного элемента оптической системы, заключённого между двумя плоскостями, перпендикулярными направлению бега световой волны и от-стоящими на расстояния z₁ и z₂ от начала расположения слоёв z = 0. Принципиальная и практическая возможность применения такого метода связана с общими свойствами электромагнитного поля, а именно: выполне-ния граничных условий для электрических (Е и D) и магнитных (В и Н) полей на границах раздела различных сред и, в частности, непрерывность касательных (тангенциальных) (τ) составляющих напряжённостей электри-ческого Е_τ и магнитного Н_τ полей световой волны и нормальных (n) составляющих индукций электрического D_n и магнитного B_n полей волны.

Электрическое поле Е(z) волны есть векторная сумма электрического вектора Е⁽⁺⁾(z) световой волны, бегущей в прямом направлении (+) оси z, и электрического вектора Е^(–)(z) световой волны, бегущей в обратном направлении оси z: Е(z) = Е⁽⁺⁾(z) + Е^(–)(z) (9.13)

причём ось z расположена перпендикулярно плоскости размещения планар-ной системы. Тогда электрические поля Е(z₁) и Е(z₂) в плоскостях z₁ и z₂, между которыми размещается рассматриваемый тонкослойный элемент перпендикулярно направлению оси z, описываются линейными соотноше-ниями в силу линейности системы уравнений Максвелла-Лоренца:

E(z₁) = SE(z₂) (9.14)

или Е⁽⁺⁾(z₁) = S₁₁Е⁽⁺⁾(z₂) + S₁₂Е^(–)(z₂) (9.15)

Е^(–)(z₁) = S₂₁Е^(–)(z₂) + S₂₂Е^(–)(z₂) (9.16)

а также E(z₁) = Е⁽⁺⁾(z₁) = S₁₁ S₁₂ Е⁽⁺⁾(z₁) (9.17)

Е^(–)(z₁) S₂₁ S₂₂ Е^(–)(z₁)

Матрица S задаёт ту часть слоистой системы,которая заключена между плоскостями, параллельными слоям оптической системы и расположенными на расстояниях z₁ и z₂ от начальной плоскости системы (z = 0).

Если координаты z₁ и z₂ лежат непосредственно по разные стороны границы раздела слоёв (j – 1) и j, то матричное соотношение (9.14) принимает специальный вид: E(z_j – 0) = I_{(j –1)j} E(z_j + 0) (9.18)

Здесь четырёхкомпонентная матрица I_(j–1)j границы раздела слоёв (j–1) и j представлена как:

I_{(j –1)j} = 1 r^*_{(j –1)j} (9.19)

r^*_{(j –1)j} 1 (t*_{(j –1)j})^–1

определяясь коэффициентами Френеля отражения r^*_{(j –1)j} и пропускания t*_{(j –1)j} для границы раздела слоёв (j–1) и j.

Если же координаты z₁ и z₂ находятся внутри слоя j при расстоянии между его границами d_j = Δz = z₂ – z₁, то имеем:

E(z_j +0) = L_jE(z_j + d_j –0) (9.20)

и L_j = exp(iβ_j) 1 (9.21). .

1 exp(–iβ_j)

где фазовый сдвиг: β_j = (2πd_jn^*_jcosθ_j/) (9.22)

и θ_j – угол направления бега световой волны к нормали на границе сред.

Искомая S-матрица слоистой системы в виде плёнки со слоями 1 и 2 на подложке 3 во внешней среде 0 дана соотношением: S = I₀₁L₁I₁₂L₂I₂₃ (9.23). . Комплексные амплитудные коэффициенты отражения R^*_p и R^*_s потока света с поляризациями р- и s-типа на слоистой системе – это отношения мат-

ричных компонент S₂₁ и S₁₁ матрицы S для линейно поляризованных частей

потока света с линейными р- и s-поляризациями: R^*_p,s = (S₂₁/S₁₁)_р,s (9.24)

Учтя формулы для матрицы I_(j–1)j границы раздела слоёв и матрицы L_j слоя среды, делают все преобразования и получают нужные для решения прямой задачи эллипсометрии данной тонкослойной системы матричные компоненты S₁₁ и S₂₁ матрицы S в виде:

S₁₁ = A^*{[1 + r^*₀₁r^*₁₂exp(–i2β₁)] + [r^*₁₂ + r^*₀₁exp(–i2β₁)]r^*₂₁exp(–i2β₂)} (9.25)

S₂₁ = A^*{[r^*₀₁ + r^*₁₂exp(–i2β₁)] + [r^*₀₁r^*₁₂ + exp(–i2β₁)]r^*₂₁exp(–i2β₂)} (9.26)

Эти матричные компоненты S₁₁ и S₂₁ матрицы S в (9.25) и (9.26) находят с точностью до фактора А^* для каждой р- и s-поляризации отражаемого света.

Различие комплексных амплитудных коэффициентов R^*_p и R^*_s для линей-но поляризованных р- и s-компонент монохроматического плоского потока света обязано, во-первых, различиями комплексных амплитудных френелев-ских коэффициентов (r^*₀₁)_p,s; (r^*₁₂)_p,s; (r^*₂₃)_p,s на границах раздела сред (0,1) для линейных р- и s-компонент и, во-вторых, набегу фаз β₁ и β₂ при толщинах d₁ и d₂ слоёв плёнки. Френелевские коэффициенты r^*_ij и фазовые сдвиги фаз β₁ и β₂ заданы значениями комплексных показателей преломления n^*₁ n^*₂ слоёв.

Но для практических применений в научных исследованиях и технологи-ческих приложениях существенный интерес представляет не прямая задача эллипсометрии, а её обратная задача. Эта обратная задача эллипсометрии состоит в том, что на основе полученных в опыте эллипсометрических углов  и Δ ищут некоторые неизвестные параметры тонкой плёнки планарной системы, в частности, толщину d₁ и показатель преломления n₁ слоя. Урав-нения для эллипсометрических углов  и Δ в прямой задаче эллипсометрии являются трансцендентными, И «обратные» для них уравнения d₁ = d₁(, Δ) и n₁ = n₁((, Δ) как аналитические решения обратной задачи эллипсометрии даже для рассмотренной нами наипростейшей тонкослойной системы полу-чить не удаётся. Но возможны при этом численные решения обратной задачи с помощью мощных быстродействующих цифровых ЭВМ.

ЛЕКЦИЯ 10. СОБСТВЕННЫЕ ПОЛЯРИЗАЦИИ ОПТИЧЕСКОЙ СИСТЕМЫ

Собственные поляризации оптической системы – это такие две поляриза-ции взаимодействующего с оптической системой потока электромагнитных ТЕ-волн, когда эти волны проходят сквозь оптическую систему без измене-нения типа поляризации. Это значит, что если на входе оптической системы поляризация потока электромагнитных ТЕ-волн была линейной или круговой (правой или левой), то и на выходе из оптической системы поляризация волн остаётся линейной с теми же направлениями колебаний электрического вектора волны или соответственно круговой с теми же правым или левым направлением вращения электрического вектора волны в плоскости наблю-дения. Собственные поляризации оптической системы можно установить на основе соображений симметрии (например, в случае оптически анизотроп-ных одноосных кристаллов) или на основе других физических соображений. И практика показывает, что соображения симметрии оказываются, как пра-вило, доминирующими. Но, видимо, исключением из этого заключения ока-зывается отражение плоского потока электромагнитных ТЕ-волн от гладкой однородной поверхности раздела диэлектрических сред, когда собственные поляризации отражателя (отражающей оптической системы) связаны с на-правлениями колебаний электрического вектора Е электромагнитной волны относительно плоскости падения (и, равноценно, отражения) потока этих волн. Да, именно, линейная поляризация р-типа отвчает тому случаю, когда электрический вектор Е в потоке электромагнитных волн колеблется в плос-кости падения/отражения, а линейная поляризация s-типа отвечает соответ-ственно случаю, когда электрический вектор Е в потоке электромагнитных волн колеблется нормально плоскости падения/отражения. Заметим, что используемые в эллипометрии обозначения для р- и s-типа собственных линейных поляризаций оптически изотропного отражателя обязаны интер-претациями типа поляризаций поперечных электромагнитных волн: р–тип обязан слову “parallelny” – параллельный – и s–тип обязан немецкому слову “strahler” – поперечный, перпендикулярный. . . В случае оптически изотропных сред, образующих границу раздела в пространстве, при отражении света под некоторым углом к этой границе раздела сред, которые предполагаются при этом не только оптически изотропными, но и оптически неактивными, не способными вращать плос-кость поляризации падающего на границу плоского потока электромагнит-ных волн, линейные поляризации р- и s-типа остаются такими же линейными поляризациями р- и s-типа и после отражения. Матрица Джонса в системе р- и s-координат для поляризаций оказывается диагональной. В результате симметрия по отношению к плоскости падения/отражения (т. е. р – в плоско-сти падения, s – перпендикулярно к ней) при отсутствии оптической актив-ности приводит к тому, что собственными поляризациями оптически изо-тропной и оптически неактивной системы как объекта эллипсометрии могут быть линейные поляризации, которые параллельны и нормальны плоскости падения/отражения. Другим примером системы с известными собственными поляризациями может быть вещественная среда, молекулы которой имеют спиральную структуру, которая порождает естественную оптическую актив-ность и так называемый круговой дихроизм (асимметрию поглощения электромагнитных волн с круговой левой и круговой правой поляризациями). Это могут быть также практически все оптически изотропные среды при их помещении в постоянное однородное магнитное поле благодаря так называ-емому магнито-оптическому эффекту Фарадея (магнитнооптическому круго-вому двулучепреломлению). В этих физических проявлениях оптической активности вещественной среды собственными поляризациями, как уже отмечалось, являются правая круговая и левая круговая поляризации. . . Оптические системы с известными собственными поляризациями можно подразделить на три типа систем в соответствии с природой их собственной поляризации: а) оптические системы с ортогональными линейными поляри-зациями, например, линейными поляризациями р- и s-типа всех оптически изотропных отражателей или линейными поляризациями, для которых элек-трический вектор Е световой волны колеблется вдоль или поперёк оптиче-ской оси одноосного кристалла; б) оптические системы с ортогональными круговыми (левыми и правыми) поляризациями, например, при распростра-нении света в средах с естественной или искусственной (наведённой) опти-ческой активностью; в) оптические системы с ортогональными эллиптиче-скими поляризациями в общем случае. Хотя линейные и круговые поляриза-ции являются частными случаями эллиптической поляризации, но многочис-ленные применения эллипсометрии для оптических систем с ортогональны-ми собственными линейными или круговыми поляризациями оказываются оправданными и весьма эффективными в соответственной конкретной прак-тической ситуации. В самом деле, в большинстве случаев использования соб-ственно эллипсометрии (т. е. поляриметрии в отражённом потоке) мы имеем дело именно с оптическими системами с ортогональными линейными собст-венными поляризациями. А в эллипсометрии пропускания, как нередко говорят, т. е. в случае собственно поляримерии, мы чаще всего сталкиваемся с ортогональными круговыми (правыми или левыми) поляризациями при распространении потока света в оптически активных средах, для которых нередко и проявление анизотропии поглощения компонент плоского потока волн с левой и соответственно правой круговыми поляризацуиями, известной как явление кругового дихроизма в оптически активных средах. . . . Оптические свойства любой оптической системы, касающиеся трансфор-мации поляризации света при его прохождении в оптической системе или в результате взаимодействя с оптической системой, описываются полностью матрицей Джонса Т оптической системы. Чтобы получить на практике, иначе говоря, измерить определяющие её элементы матрицы Т_ij (i, j = 1, 2), мы пользуемся тем важным фактом, что эллипсы поляризации падающей или входной (i) и выходящей (е) световых волн (независимо от их амплитуды и фазы) описываются комплексными переменными _i и _e (определёнными собственными поляризациями оптической системы). Вспомним при этом, что эллипсы поляризации на входе (i) и выходе (е) оптической системы описыва-ются этими переменными, которые в свою очередь задаются по договорён-ности соотношениями вида: _i = (E_iy/E_ix) (10.1). .

_ie = (E_ey/E_ex) (10.2).

где E_iy и E_ix, E_ey и E_ex – проекции электрического вектора Е световой волны вдоль координатных осей у и х на входе (i) и выходе (е) оптической системы. И функциональная связь между входной _i и выходной _e комплексными переменными эллипса поляризации потока света на входе (i) и выходе (е) оптической системы выражена через соответственные элементы Т_ij (i, j = 1, 2) матрицы Джонса Т системы: . . _e = (Т₂₂_i + Т₂₁)/(Т₁₂_i + Т₁₁) (10.3). . Это билинейное преобразование (10.3) однозначно определено отображе-нием трёх входных поляризаций (_i1, _i2, _i3) в соответствующие три выход-ные поляризации (_е1, _е2, _е3): .

[(_e – _e1)(_e3 –_e2)]/[(_e –_e2)(_e3 –_e1)] = . . = [(_i – _i1)(_i3 – _i2)]/[(_i – _i2)(_i3 – _i1)] (10.4). . Преобразовав это соотношение (10.4) так, что оно принимает форму (10.1), можно получить значения элементов Т_ij (i, j = 1, 2) матрицы Джонса Т систе-мы с точностью до постоянного комплексного множителя А^_о, учитываю-щего в общем случае амплитуду А_о и фазу _о световой волны: . .

Т₁₁ = _i2 – _i1Н (10.5). .

Т₁₂ = Н – 1 (10.6). .

Т₂₁ = _i2 _i2 – _i1_e2Н (10.7). .

Т₂₂ = – _e1 + _e2Н (10.8). .

Н = [(_e3 –_e1)(_i3 – _i2)]/[_e3 –_e2)(_i3 – _i2)] (10.9).

. В большинстве случаев, имеющих теоретический или практический инте-рес, значение постоянного множителя А^_о, с точностью до которого опреде-ляются значения элементов Т_ij (i, j = 1, 2) матрицы Джонса Т системы, можно опустить, если воспользоваться представлением нормированной матрицы Джонса Т_норм с её нормированными элементами Т_ij, которые получаются делением величины элемента Т_ij (i, j = 1, 2) матрицы Джонса Т системы на величину её элемента Т₂₂  0: (Т₁₁/Т₂₂), (Т₁₂/Т₂₂), (Т₂₁/Т₂₂) и 1 (10.10). .

Фунциональную зависимость комплексной величины _e на выходе оптиче-ской системы от комплексной величины _i3 на входе оптической системы принято называть поляризационной передаточной функцией (ППФ) системы. Как отмечалось, она представляет собой билинейное преобразование (10.3), коэффициенты которого Т_ij (i, j = 1, 2) и есть элементы Т_ij матрицы Джонса. . . Поляризационная передаточная функция даёт полное представление о том, как оптическая система преобразует входящий в неё световой поток для всех его возможных поляризаций, и, наоборот, полное представление о состояниях поляризации входящего в оптическую систему потока на основе данных состояний потока света на выходе из оптической системы:

_i = [T₁₁_e – T₂₁]/[ –T₁₂_e + T₂₂] (10.11). . Итак, соотношение (10.11) даёт эллипс поляризации _i входящего в оптическую систему потока света, если известен эллипс поляризации _е на выходе оптической системы. Так, если известен отклик оптической системы (т. е. известна поляризации света на выходе оптической системы) на три раз-личных поляризации (_i1, _i2, _i3) входящего потока волн, то отклик _e опти-ческой системы на все другие поляризации входящего потока (i) полностью определены согласно приведённому ранее соотношению (10.4). Полагая (_i = _е =  и решая уравнение:

Т₁₂² + (Т₁₁ – Т₂₂) – Т₂₁ = 0 (10.12).

находим: _е1,2 = {(T₂₂ – T₁₁ )  [(T₂₂ – T₁₁ )² + 4T₁₂T₂₁]^1/2}/(2T₂₂) (10.13).