Универсальный генератор случайных реализаций св

Выполнить обратное преобразование F^–1() можно далеко не для всех распределений. В таких случаях эффективны процедуры прямого вычисления, использующие не математические преобразования, а вероятностную природу распределения. Например, для генерации случайного числа, подчиненного биномиальному закону с параметрами n, p, проводят n испытаний Бернулли (n независимых случайных чисел сравнивают с p) и суммируют число успехов. Реализацию СВ, подчиненной закону Пуассона с параметром  получают как минимальное количество случайных чисел (минус 1), произведение которых меньше, чем exp( –), а реализацию геометрического распределения с параметром p – как целую часть величины (ln rand / ln(1 – p)).

Функция Gen (Листинг 3.2) возвращает случайные реализации всех практически интересных распределений, сокращенное название которых ('bin' – биномиальное, 'geo' – геометрическое, 'poi' – Пуассона, и т.д.) задано первым аргументом. Далее следуют параметры закона в определенном порядке, если их нельзя различить по значениям, как, например, параметры биномиального закона n > 1, p < 1. Последним аргументом Gen задается количество требуемых случайных чисел. Для примера получим 15 случайных реализаций СВ, распределенной по биномиальному закону с параметрами n = 6, p = 0,4:нерируемых случайных чисел. Получим 15 случайных реализаций СВ, рае 0000000000000000000000000000000000000

>> X=Gen('bin',0.4,6,15), Y=Gen('bin',6,0.4,15)

X = 2 2 4 4 5 1 2 2 2 3 1 2 4 0 4

Y = 3 2 1 4 1 3 2 0 1 5 1 2 2 3 0

Оба выражения определены корректно, результаты X и Y различаются как случайные реализации двух серий испытаний Бернулли с вероятностью успеха 0,4.

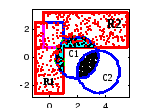
Рис. 3.13. Равномерное распре­деление точек

В отличие от random из библиотеки MATLAB функция Gen умеет работать с объектами, что важно для статистического моделирования. Например, можно разыграть равномерное распределение в прямоугольнике, круге (фигурах, производных от класса SmartShape), на их пересечениях и объединениях (рис. 3.13):

>> R1=Rect(2,5);R2=Rect(6,2,[3;2]);C=Circ([2;0],2);C2=C+[2;-1];

>> Z=Union(R1,R2); S1=Sect(C,C2); S2=Sect(Z,C);

>> a=Gen('rnd',Z,500);c1=Gen('rnd',S1,300); c2=Gen('rnd',S2,200);

>> Show(R1,R2,C,C2,Z,'Fc',S1,a,'r.',c1,'k.',c2,'k.')

Статистические распределения

Эмпирическая функция распределения

Закон распределения длины проекции стержня построен на основании предположения о равновероятных угловых положениях. Если априорные сведения, необходимые для построения зависимости вероятности P(X < x) от x отсутствуют, но реализации СВ X можно наблюдать в специально поставленном эксперименте (или в явлениях природы), набирают статистику X_j,  j = 1, …, N и строят эмпирическую функцию распределения F^*(x) по относительной частоте реализаций X, меньших, чем x:

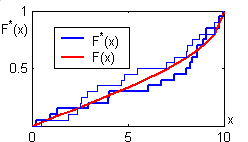
Рис. 3.8. Эмпирическая и теоретическая функции распределения

F^*(x) = .

Проведем экспери­мент: разыграем N = 20 случайных углов в интервале [0, /2] и вычислим соответствующие им длины проекции стержня. В реальном эксперименте распределение случайных углов может быть неизвестным, а длины пробоин измеряются с некоторой случайной погрешностью. Построим график относительных частот с разрывами в реализациях и горизонтальными участками между ними (рис. 3.8):

>> L=10; N=20; x=rand(1,N)*pi/2;X=sort(sin(x))*L;

>> y=[0 X];y=sort([y,y]);z=(0:N)/N;Z=[z;z];Z=Z(:)';plot(y(2:end),Z(1:end-1), u, F(2:end-1))

Если выполнить эти же команды повторно, получим другой график, не совпадающий с первым из-за случайности реализаций при небольшом объеме статистики (тонкая линия на рис. 3.8). Для сравнения на тот же график выведена теоретическая функция распределения.