- •Лекция 3 Случайные величины
- •Случайные величины как факторы случайности событий
- •Определение случайной величины
- •Дискретные случайные величины
- •Свойства дискретных распределений
- •Индикатор случайного события
- •Закон распределения дискретных св
- •Биномиальное распределение
- •Распределение Пуассона
- •Геометрическое распределение
- •Гипергеометрическое распределение
- •Непрерывные случайные величины
- •Вероятностный смысл функции распределения непрерывной св
- •Свойства функции распределения
- •Плотность распределения
- •Основное свойство плотности распределения
- •Дискретно-непрерывные св
- •Пример построения закона распределения
- •Практическое использование законов распределения
- •Интегральная формула полной вероятности
- •Какая нужна технология обработки законов распределения
- •Получение случайных реализаций св согласно ее закону распределения
- •Универсальный генератор случайных реализаций св
- •Статистические распределения
- •Эмпирическая функция распределения
- •Эмпирический закон распределения дискретной св
- •Гистограмма частот
- •Построение гистограммы
- •Построитель гистограмм
- •Оптимизация гистограмм
- •Статистическая функция распределения
- •Построение закона распределения дискретной св
- •Моделирование дискретно-непрерывных случайных величин
- •Пример дискретно-непрерывной св
- •Полиморфизм объектных методов
- •БэсПиБп.3. Случайные величины 15
Закон распределения дискретных св
![]()
Поскольку события (X = xi) составляют полную группу, их можно рассматривать как гипотезы для события A, вероятность которого зависит от xi. Формулу полной вероятности можно выразить через ряд распределения и условные вероятности P(A|X = xi) P(A|xi):
|
P(A) =
|
(3.1) |
Биномиальное распределение
|
Таблица 3.1. Ряд распределения |
||||||||||
|
||||||||||
|
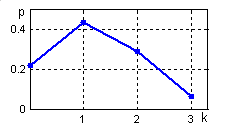
Рис. 3.1. Многоугольник биномиального распределения |
>> p= p_Binom(0.4,3),plot(0:3,p)
p = 0.2160 0.4320 0.2880 0.0640
Распределение числа успехов в испытаниях Бернулли называется биномиальным законом распределения:
|
P(X = k) =
pk
=
|
(3.1) |
Условия, которым должно удовлетворять распределение, выполнены:
pk
> 0,
![]() pk(1–p)n – k =
(p + 1 –
p)n
= 1.
pk(1–p)n – k =
(p + 1 –
p)n
= 1.
Распределение Пуассона
|
P(X = k) =
pk
=
|
(3.2) |
Легко проверить, что сумма членов бесконечного ряда pk сходится к 1:
|
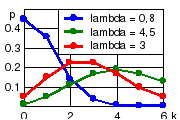
Рис. 3.2. Распределение Пуассона |
На рис. 3.2 показаны характерные многоугольники распределения Пуассона с параметрами = 0,8, целом = 3 и = 4,5, построенные с помощью электронной формулы p_Poisson следующей командой:
>> k=0:6;plot(k,p_Poisson(0.8,k),k,p_Poisson(4.5,k),k,p_Poisson(3,k))