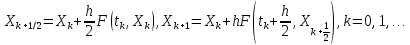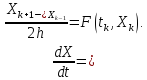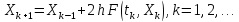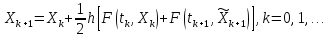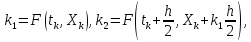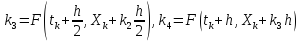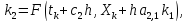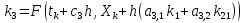2. Явные численные методы решения обыкновенных дифференциальных уравнений

1. Явный метод Эйлера

Метод Эйлера являлся исторически первым методом численного решения задачи Коши. О. Коши использовал этот метод для доказательства существования решения задачи Коши. Ввиду невысокой точности и вычислительной неустойчивости для практического нахождения решений задачи Коши метод Эйлера применяется редко. Однако в виду своей простоты метод Эйлера находит свое применение в теоретических исследованиях дифференциальных уравнений, задач вариационного исчисления и ряда других математических проблем.

Метод Эйлера — наиболее простой численный метод решения (систем) обыкновенных дифференциальных уравнений. Впервые описан Леонардом Эйлером в 1768 году в работе «Интегральное исчисление»[1]. Метод Эйлера является явным, одношаговым методом первого порядка точности, основанном на аппроксимации интегральной кривой кусочно-линейной функцией, так называемой ломаной Эйлера.

Точность расчета метода Эйлера зависит от размера шага линейно, зависимость точности от шага - первой степени. То есть, чтобы увеличить точность в 10 раз, надо уменьшить шаг в 10 раз. На практике интересны более совершенные методы. Таким методом является модифицированный метод Эйлера. Модифицированный метод Эйлера имеет точность второго порядка.

2. Модифицированный метод Эйлера

Идея уточненного метода Эйлера состоит в том, что производную вычисляют не в k-ой точке, а между двумя соседними точками: k и k + 1.

Формулы для вычисления приближенного для вычисления приближенного решения имеют вид:

(17)

3. Метод Эйлера – Коши

Для конечно-разностной аппроксимации производной в системе (12) воспользуемся следующей формулой:

Тогда

(18)

Соотношение (18) представляет собой алгоритм приближенного решения системы (12), называется методом Эйлера-Коши. Этот метод имеет второй порядок точности.

4. Метод предсказания и коррекции

Метод предсказания и коррекции состоит из двух взаимосвязанных этапов.

1. Предсказание. Находится приближенное значение точки X(t_k+1) явным методом Эйлера:

   (19)

2. Коррекция. Точка 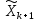уточняется (корректируется) по формуле

(20)

Метод имеет второй порядок точности относительно шага h.

5. Явные методы Рунге-Кутта

Формула для вычисления X(t_k+1) методом Рунге-Кутты четвертого порядка имеет следующий вид:

(21)

где k₁, k₂, k₃, k₄ – угловые коэффициенты касательных к графику решения в различных точках, вычисляемые по формулам

(22)

Метод имеет четвертый порядок точности относительно шага h.

Метод Рунге-Кутты, как и метод Эйлера, является одношаговым, так как значение 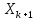вычисляется на основе текущего значения . Этот метод ограниченно устойчив. По сравнению с методом Эйлера здесь на одной итерации требуется вычислять значение правой части системы (12) четыре раза. Как и явный метод Эйлера, метод Рунге-Кутты не требует дополнительных разгонных точек, что позволяет легко менять шаг в процессе вычислений. Для повышения устойчивости ограниченно устойчивых методов могут использоваться серии шагов разной величины. Например, в двухшаговой серии первый шаг h₁ может быть большим, а второй h₂ - малым и так далее. При таком подходе неустойчивость, если она возникнет на первом шаге, уменьшается на втором, а средний шаг превышает h_kp.

В общем случае методы Рунге-Кутты описываются набором соотношений следующей структуры:

……………………………………………………

(23)

где s – число стадий (этапов); k₁, …, k_s – значения, вычисленные на основе правой части системы (12); c₁, …, c_s; a_l,m, l = 2, …, s; m = 1, …, s-1; b₁, …, b_s – коэфициентф схемы Рунге-Кутты.

Многие из описываемых схем включает также соотношение для нахождения приближения , порядок точности которого на единицу больше или меньше порядка, обеспечиваемого с помощью 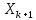. Величина служит для учета погрешности и управления величиной шага.