ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
Государственное образовательное учреждение
высшего профессионального образования
«ТОМСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
«Утверждаю»
Зам. начальника учебного отделения по ЗО ИГНД
______________В.И. Брылин
«____»_____________2004г.
Сопротивление материалов
Методические указания по выполнению контрольных заданий для студентов специальностей 090600 «Разработка и эксплуатация нефтяных и газовых месторождений», 090800 «Бурение нефтяных и газовых скважин»
Томск 2004
УДК 53
Сопротивление материалов. Методические указания по выполнению контрольных заданий. – Томск: Изд-во. ТПУ, 2004. – 62с.
Составители: профессор, д.ф.-м.н. Светашков А.А. доцент, к.т.н. Цукублина К.Н. ассистент Харченко Д.А.
Рецензент: доцент, к.т.н. Н.А. Куприянов
Методические указания рассмотрены и рекомендованы к изданию методическим семинаром кафедры теоретической и прикладной механики
Протокол № 32 от 18 октября 2003г.
Зав. Кафедрой ТПМ
доцент, к.т.н. В.М. Замятин
Одобрено учебно-методической комиссией ИГНД.
Председатель методической комиссии
И.М. Наливайко
Содержание
Задача №1. Растяжение и сжатие 4
Порядок выполнения и методические указания к задаче №1 4
Пример решения задачи №1 4
Задача №2. Расчет статически неопределимых систем 6
Порядок выполнения и методические указания к задаче №2 7
Пример решения задачи №2 7
Задача №3. Исследование напряженно деформируемого состояния 8
Порядок выполнения и методические указания к задаче №3 9
Пример решения задачи №3 9
Задача №4. Кручение бруса круглого поперечного сечения 12
Порядок выполнения и методические указания к задаче №4 12
Пример решения задачи №4 12
Задача №5. Геометрические характеристики плоских сечений 15
Порядок выполнения и методические указания к задаче №5 16
Пример решения задачи №5 18
Задача №6. Изгиб. Определение внутренних усилий, расчет на прочность. Определение размеров поперечного сечения балки 20
Порядок выполнения и методические указания к задаче №6 20
Пример решения задачи №6 20
Задача №8. Внецентренное растяжение, сжатие 25
Порядок выполнения и методические указания к задаче №8 25
Пример решения задачи №8 27
Задача №9. Расчет ломаного бруса 31
Пример решения задачи №9 32
Сложное сопротивление. Совместное действие изгиба и кручения 35
Задача №10 37
Пример решения задачи №10 37
Расчет статически неопределимых рам 42
Пример решение задачи №11 44
Устойчивость сжатых стержней 50
Пример решение задачи №12 51
Упругие колебания 54
Пример решение задачи №13 55
Динамическое действие нагрузок. Учет сил инерции 57
Порядок решения задачи №15 57
Пример решения задачи №15 57
Задача №1. Растяжение и сжатие.
Стальной стержень
находится под действием продольной
силы
и собственного веса. Найти перемещение
сечения А – А и свободного конца
стержня.
Д
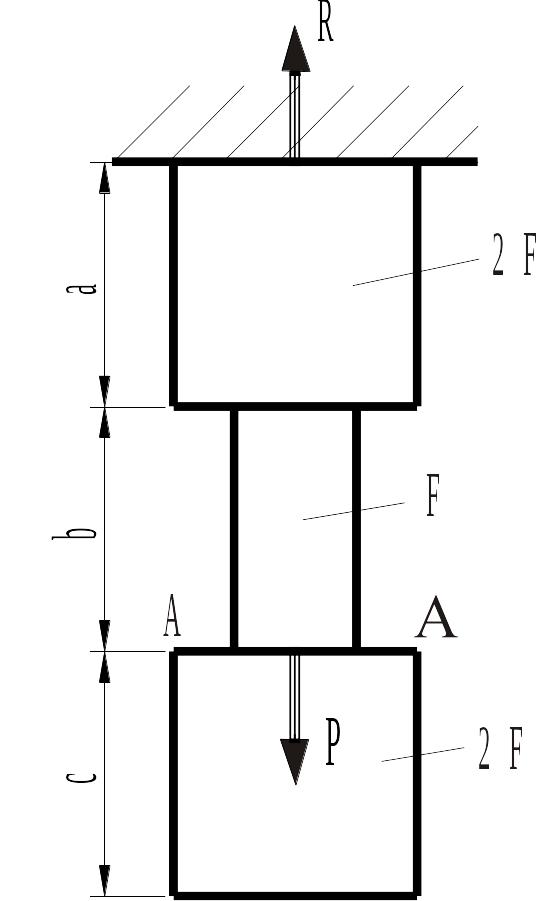ано:
,
,
,
,
,
,
Рис. 1.1.
Порядок выполнения и методические указания к задаче №1.
1. Вычертить расчетную схему в масштабе.
2. Определить продольные усилия методом сечений.
3. Построить эпюру
распределения внутренних усилий
.
4. Построить эпюру
перемещений
.
Искомое перемещение определяется относительно неподвижного сечения и зависит от деформации участков, расположенных между опорами и заданным сечением.
Собственный вес
части стержня
рассматривать как внешнюю нагрузку.
Деформация от
собственного веса участков
и
определяется соотношением
,
где 
– вес соответствующего участка,
– длина участка,
– площадь его поперечного сечения,
– модуль упругости I рода.
Собственный вес
,
где
– удельный вес материала.
Пример решения задачи №1.
а) Определение внутренних усилий.
Проводим сечения на каждом участке, где меняется или меняется внешняя нагрузка (рис. 1.2.).
Сечение
1 – 1 
(рис. 1.2. а)
,
Т.к.
зависимость
от
линейная, эпюру можно построить по двум
точкам при
,
;
при
,
.
Сечение 2 –
2 
(рис.
1.2. б)
,
.
При
,
;
при
,
.
Сечение 3 –
3 
(рис. 1.2. в)
,
При
,
;
при
,
.
По полученным значениям строим эпюру (рис. 1.2. г.)
В сечении, где
действует сила
,
на эпюре
наблюдается скачек, равный по величине
силе
.
б) Определение
перемещения сечения А – А
.
Перемещение зависит от деформаций участков , , расположенных между опорой и рассматриваемым сечением.
– деформация
участка
от собственного веса
плюс деформации от действия трех сил:
,
,
,
выраженные по закону Гука.
– деформация участка происходит под действием собственного веса и под действием двух сил: и .
в) Перемещение свободного конца стержня
.
Построение эпюры
перемещения следует начинать с опорного
сечения, где
.
Рассчитаем перемещение в сечении В – В:
;
в сечении A – A:
;
и на свободном конце
.
Здесь
– деформация участка
от собственного веса
:
Эпюра перемещений показана на рис. 1.2. д.
Рис. 1.2.
Задача решена.
Задача №2. Расчет статически неопределимых систем.
Абсолютно жесткий
брус опирается на шарнирно неподвижную
опору в точке
и скреплен с двумя стержнями при помощи
шарниров
и
(рис. 2.1. а).
Дано: 
,
,
,
,
,
,
,
,
,
.
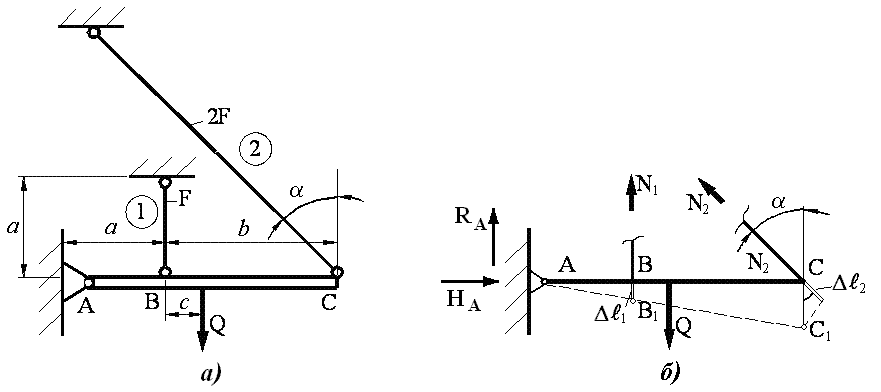
Рис. 2.1.
Требуется: 1)
Найти усилия и напряжения в стержнях;
2)
Найти допускаемую нагрузку
.
Порядок выполнения и методические указания к задаче №2.
Вычертить расчетную схему в масштабе (рис. 2.1. а).
Рассмотреть и изобразить картину возможных перемещений (рис. 2.1. б).
Записывая уравнения статики, найти степень статической неопределимости задачи, т.е. количество неизвестных, превышающих число уравнений равновесия.
Составить необходимое число дополнительных уравнений, выражая геометрическую зависимость между деформациями.
Решая совместно эти уравнения (после выражения перемещений через искомые усилия по закону Гука) с уравнениями статики, определить усилия в стержнях в долях .
Выразить напряжения в стержнях и ограничить большее из них допускаемым напряжением. Найти
.
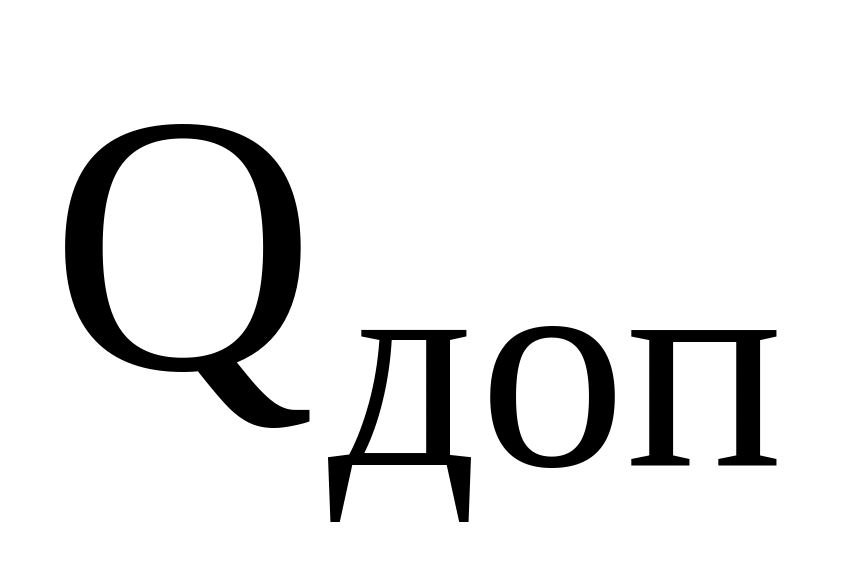Пример решения задачи №2.
Под действием
нагрузки
в стержнях 1, 2 возникают растягивающие
усилия
,
,
а в опоре реакции
,
.
Неизвестных – 4. Освободим брус от
связей, заменив их усилиями. Записываем
условия равновесия системы (уравнения
статики) – их 3:
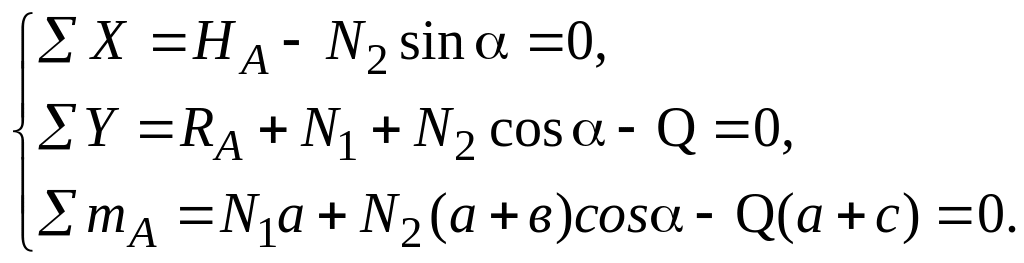(1)
Задача один раз
статически неопределима. Дополнительное
уравнение получим, рассматривая картину
возможных перемещений (рис. 2.1. б).
В результате растяжения стержней 1, 2
жесткий брус смещается в положение
.
Пренебрегая горизонтальными смещениями
узлов
и
и считая угол наклона стержня 2 не
изменившимся, найдем из подобия
треугольников
и
:
или
(2)
по закону Гука:
,
.
Подставляя в (2), получим, учитывая , :
или
. (3)
Далее решая совместно систему (1) и (3), получаем:
,
,
,
.
Условие прочности проверяем по большему напряжению:
,
отсюда
,
.
Задача решена.
Задача №3. Исследование напряженно деформируемого состояния.
Стальной кубик (рис. 3.1. а.) находится под действием сил, создающих плоское напряженное состояние.
Требуется определить:
1) Главные напряжения и положение главных площадок графически (с помощью круга Мора) и аналитически;
2) Деформации
;
3) Максимальные касательные напряжения;
4) Относительное изменение объема;
5) Удельную потенциальную энергию.
Порядок выполнения и методические указания к задаче №3.
Вычертить расчетную схему.
Проанализировать знаки напряжений.
Вести последующие вычисления с учетом знаков напряжений.
Пример решения задачи №3.
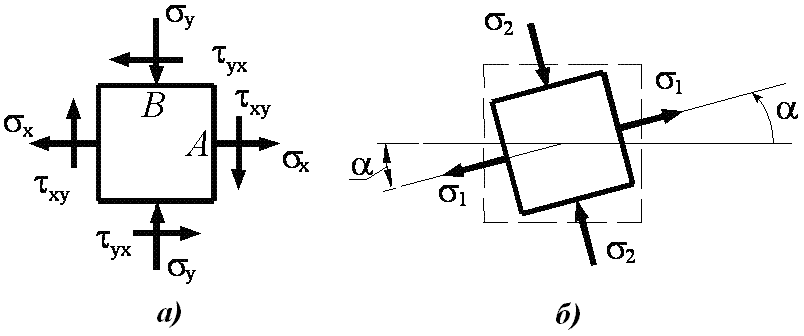
Рис. 3.1.
Устанавливаем знаки напряжений, модули которых указаны в таблице исходных данных. В соответствии с правилом знаков нормальные растягивающие напряжения положительны, сжимающие – отрицательны. Касательные (сдвиговые) напряжения положительны, если они вращают положительную нормаль к площадке по часовой стрелке.
На
схеме
,
(что соответствует закону парности
сдвиговых напряжений).
Следовательно,
,
,
.
Определяем главные напряжения и положение главных площадок при помощи круга Мора (рис. 3.2.):
а) проводим
оси
,
;
б) откладываем
по оси абсцисс,
так, что точка
имеет координаты
и соответствует площадке
;
в) откладываем
,
– получаем точку
;
г) соединяем
точки
и
прямой, находим точку
на пересечении
с осью
;
д) из
точки
радиусом
проводим круг;
е) точки
пересечения круга с осью
дадут:
,
;
ж) значения
,
можно определить, зная масштаб;
з) угол:
,
,
где
– угол между главной площадкой с
и площадкой
.
Значения главных
напряжений и угла
аналитически:
,
.
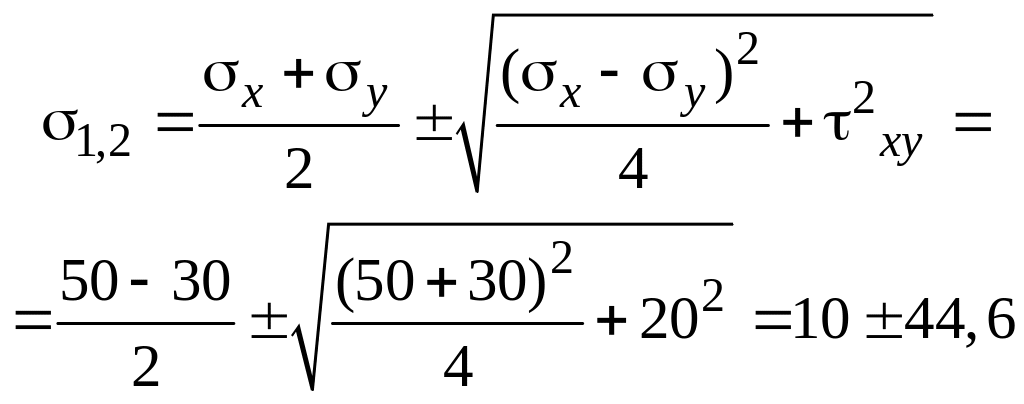
Сопоставляя
найденные
с отрезками
,
круга Мора, убеждаемся в совпадении (с
точностью до графических построений)
двух способов расчета.
Положение главных площадок определяется углом
,
,
.
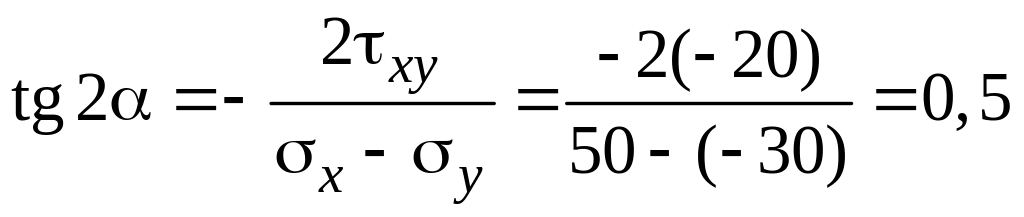Положительный
угол
откладываем против часовой стрелки от
площадки с большим (по алгебраическому
значению) напряжением. При
откладываем угол
от
(рис. 3.1. б).
Максимальное касательное напряжение определяется:
.
действует по
площадкам, наклоненным под углом
к главным.
Относительное изменение объема
.
По закону Гука деформации в направлении осей
,
,
,
.
Знак
плюс у
указывает, что объем в результате
деформации увеличивается.
Удельная потенциальная энергия деформации
,
,
.
Рис. 3.2.
Задача решена.
Задача №4. Кручение бруса круглого поперечного сечения.
Порядок выполнения и методические указания к задаче №4.
Вычертить расчетную схему в масштабе. Предусмотреть место под схемой для построения эпюр крутящих моментов и углов закручивания.
Выразить угол поворота правого концевого сечения, используя принцип независимости действия сил и закон Гука. Приравнять полученную суммарную деформацию нулю и выразить величину момента Х.
Построить эпюру крутящих моментов, применяя метод сечений.
Из условия прочности определить диаметр вала:
,
,
.
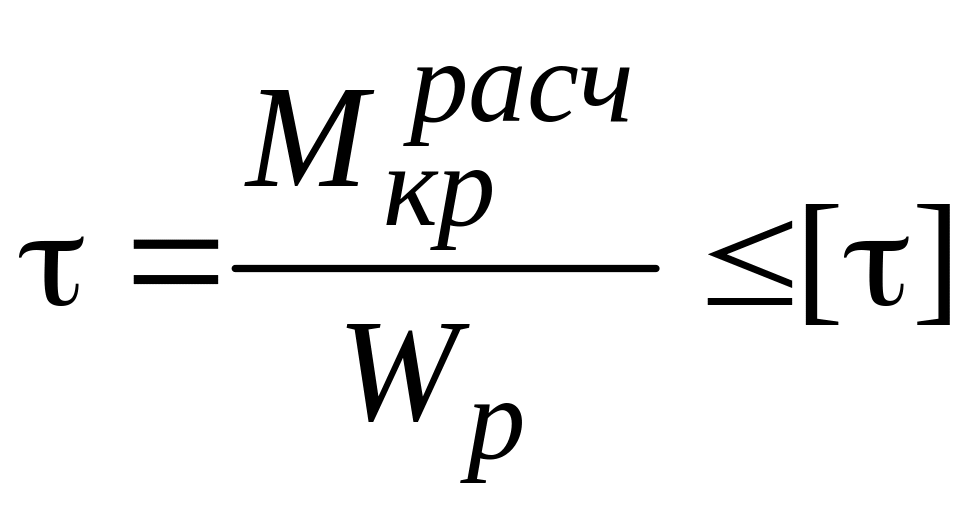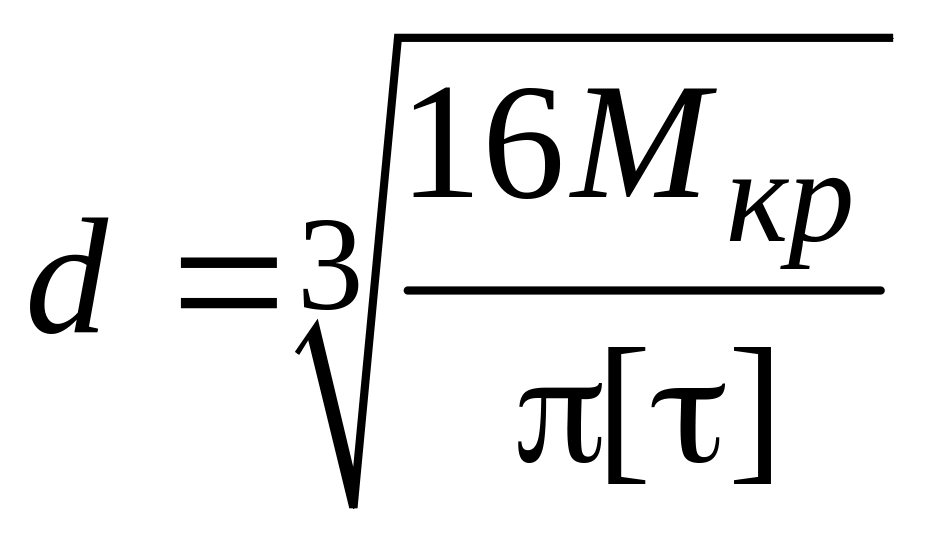Значение расчетного момента берется с эпюры крутящих моментов.
Определить углы закручивания отдельных участков вала, принимая сечение, где вал закреплен неподвижным. Угол закручивания определяется по закону Гука:
,
где
– длины участков вала,
– соответствующее каждому участку
значение крутящего момента с эпюры
.
Пример решения задачи №4.
Дано: 
,
,
,
,
,
,
,
Рис. 4.1.
Стальной вал
подвергается воздействию крутящих
моментов
,
,
,
.
Требуется: а) определить
крутящий момент
в сечении Е при условии, что угол поворота
;
б) построить эпюру крутящих моментов;
в) определить диаметр вала из условия прочности;
г) построить эпюру углов закручивания.
Решение:
1. Проставляем
реакцию в опоре
–
.
Таким образом на рассматриваемую систему действуют два неизвестных момента и .
Записываем условие равновесия системы (уравнения статики)
. (1)
Задача статически неопределима.
В соответствии с принципом расчета статически неопределимых систем рассматриваем возможное перемещение свободного конца вала. Поворот сечения Е можно представить как сумму перемещений этого сечения от каждого из крутящих моментов, действующих на вал:
. (2)
По условию задачи
.
Здесь: 
,
,
,
. (3)
Подставляя (3) в уравнение (2) получаем:
,
.
Из
соотношения (1) следует
.
2. Строим эпюру крутящих моментов.
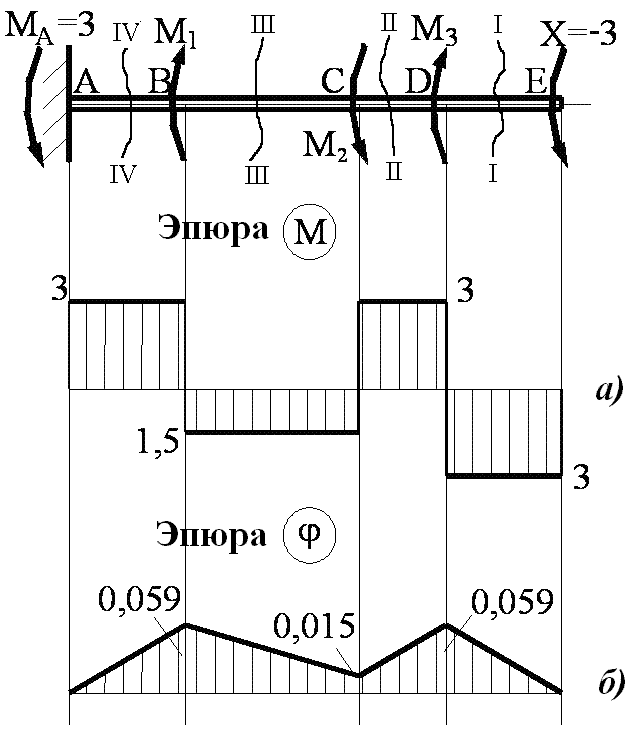
Рис. 4.2.
При определении внутренних усилий используем метод сечений. Внутренний момент в сечении равен сумме внешних моментов, расположенных по одну сторону от рассматриваемого сечения.
На представленной схеме следует рассматривать четыре сечения. Подходим к каждому сечению справа.
Сечение I
– I : 
.
Сечение II
– II : 
.
Сечение III
– III : 
.
Сечение VI
– VI : 
.
Построив эпюру внутренних скручивающих моментов (рис. 4.2. а), видим:
.
3. Определяем диаметр вала из условия прочности
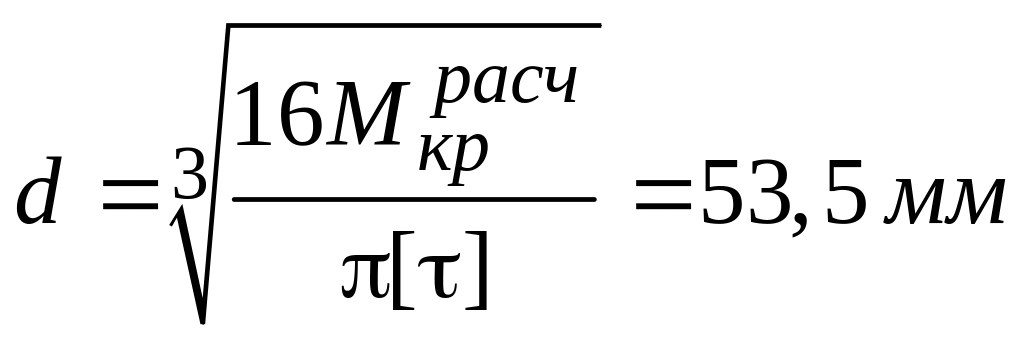
округляем
его, исходя из ряда предпочтительных
чисел
.
4. Строим эпюру углов закручивания (рис. 4.2. б).
Определяем жесткость вала:
Угол поворота в сечении A равен нулю, т. к. это опорное сечение.
На участке AB
действует внутренний скручивающий
момент
.
Угол поворота в сечении B по отношению к сечению A равен
.
Поворот сечения С относительно сечения А:
.
Поворот сечения D относительно сечения A:
Поворот сечения E относительно сечения A:
Эпюра углов закручивания представлена на рис. 4.2. б.
Задача решена.
Задача №5. Геометрические характеристики плоских сечений.
Для
заданного поперечного сечения, состоящего
из швеллера №20 и равнобокого уголка
,
требуется:
1. Определить положение центра тяжести (ЦТ);
2. Найти величины осевых и центробежного моментов инерции относительно произвольных осей, проходящих через ЦТ;
3. Определить положение главных центральных осей;
4. Найти моменты инерции относительно главных осей.
Выписываем характеристики швеллера и уголка из таблиц сортаментов.
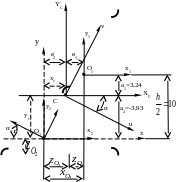
Рис. 5.1.
Характеристики профилей:
Швеллер №20:
;
,
,
,
,
.
Уголок :
,
,
,
,
,
Порядок выполнения и методические указания к задаче №5:
1. Вычертить расчетную схему, показать все размеры в буквах и числах. Указать оси, проходящие через центр тяжести (ЦТ) каждого профиля.
2. Для определения
положения ЦТ сечения выбрать вспомогательную
систему координат
.
Рекомендуется, чтобы эта система совпала
с главными осями инерции одного из
профилей.
3. Через найденный
ЦТ параллельно вспомогательным осям
провести центральные оси сложного
составного сечения
,
.
4. Обозначить и вычислить расстояние между центральными осями составляющих сечений и осями , .
5. Определить осевые и центробежный момент инерции составного сечения относительно центральных осей , , пользуясь теоремой о параллельном переносе осей.
6. Определить
положение главных осей инерции
,
по формуле:
.
Положительное значение соответствует повороту осей , по направлению от оси с меньшим моментом инерции – к оси с большим моментом инерции.
7. Определить величины моментов инерции относительно главных центральных осей и , пользуясь формулами перехода от осей , к осям, повернутым относительно них на угол .
8. Произвести проверку, исходя из того положения, что сумма моментов инерции относительно любой пары осей есть величина постоянная.
Известно
,
.
Здесь
,
– статические моменты сечения относительно
осей
и
.
,
.
В выбранной системе отсчета
, 
,
, 
.
Пример решения задачи №5
Заданное сечение представлено на рис. 5.1.
1. Определение центра тяжести составного сечения (ЦТ).
Выбираем
вспомогательные оси
,
совпадающие с системой центральных
осей уголка
,
:
,
.
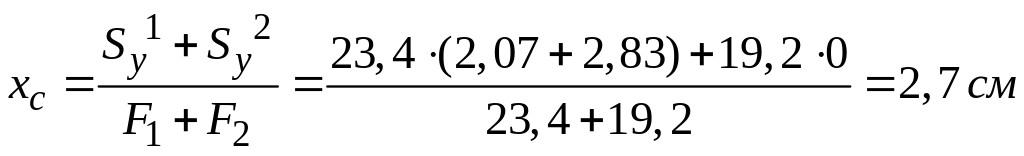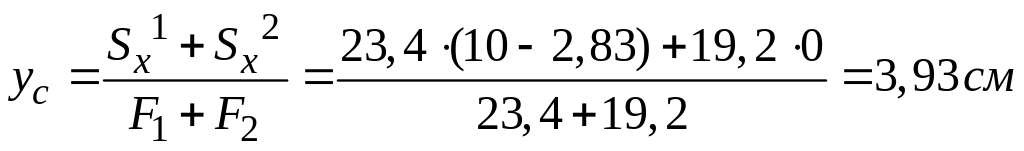Наносим точку на чертеже. При правильном определении положения ЦТ точка лежит на прямой, соединяющей ЦТ уголка и швеллера.
2. Определение осевых и центробежного моментов инерции относительно осей , .
Проведем оси , параллельно собственным центральным осям швеллера и уголка. Обозначим расстояния между осями и вычислим их. При этом учтем, что теперь за основные принимаются оси , , поэтому все расстояния, отложенные вверх и вправо, считаем положительными, вниз и влево – отрицательными.
,
,
,
.
Момент инерции составного сечения равен сумме моментов инерции составляющих сечений:
,
,
.
Пользуясь формулами определения моментов инерции относительно параллельных осей, находим:
,
,
,
,
,
.
Центробежный момент инерции:
Здесь
,
т.к. оси
,
являются главными осями швеллера.
Центробежный момент инерции уголка:
3. Определение положения главных осей. Угол наклона осей инерции к центральным определяется соотношением:
,
,
,
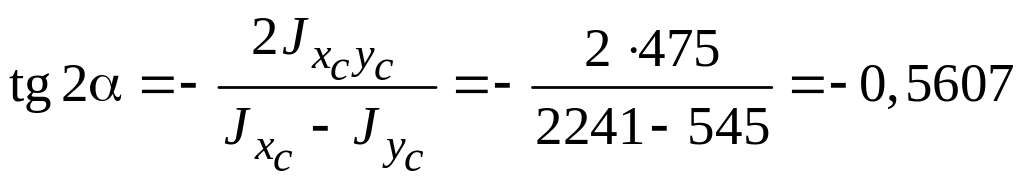откладываем
угол
по направлению от оси
к оси
.
Положение главных осей приведено на
рис. 5.1. – оси
,
.
4. Определение главных моментов инерции сечения:
,
,
.
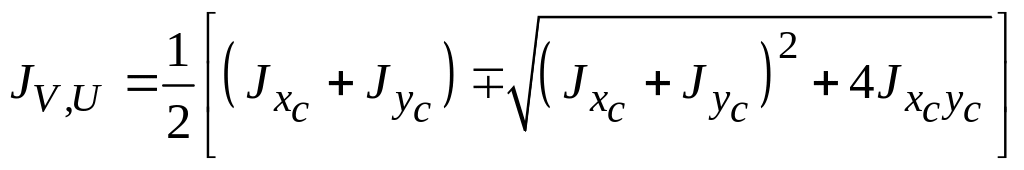Известно, что сумма осевых центральных моментов при повороте осей остается неизменной.
Проверим:
,
,
,
что требовалось доказать.
Следовательно,
моменты инерции
,
определены верно.
Задача решена.
Изгиб. Определение внутренних усилий, расчет на прочность. Определение размеров поперечного сечения балки.
Порядок выполнения и методические указания к задаче №6.
1. Вычертить расчетную схему балки в масштабе с указанием всех размеров и усилий, действующих на балку. Проставить опорные реакции.
2. Выявить количество силовых участков. Новый силовой участок начинается там, где появляется новое усилие, либо меняется характер нагружения, либо меняются жесткостные характеристики балки.
3. Выполнить
необходимое количество сечений и указать
переменную абсциссу
для каждого из них.
4. Записать функции перерезывающей силы и изгибающего момента от переменной абсциссы в общем виде. Здесь же указать границы участка (значения ), в пределах которых действительна записанная функция. Функции представить графически.
Перерезывающая сила в сечении равна алгебраической сумме проекций на вертикальную ось всех внешних сил, лежащих по одну сторону от рассматриваемого сечения. Положительной будем считать силу, находящуюся слева от сечения и направленную вверх, или силу, находящуюся справа от сечения и направленную вниз.
Изгибающий момент в сечении равен алгебраической сумме моментов всех внешних сил, расположенных по одну сторону от рассматриваемого сечения. Момент внешних сил, взятый относительно точки, расположенной в сечении, считается положительным, если он сжимает верхние слои балки, и отрицательным, если сжаты нижние слои балки.
Построение эпюр перерезывающих сил и изгибающих моментов для консольных балок предпочтительней вести ходом со свободного конца.
Пример решения задачи №6
Схема балки представлена на рис. 6.1. а.
Дано:
;
;
;
.
Требуется: 1. Построить эпюры перерезывающих (поперечных) сил и изгибающих моментов .
2. Определить из условия прочности необходимый момент сопротивления, поперечного сечения балки.
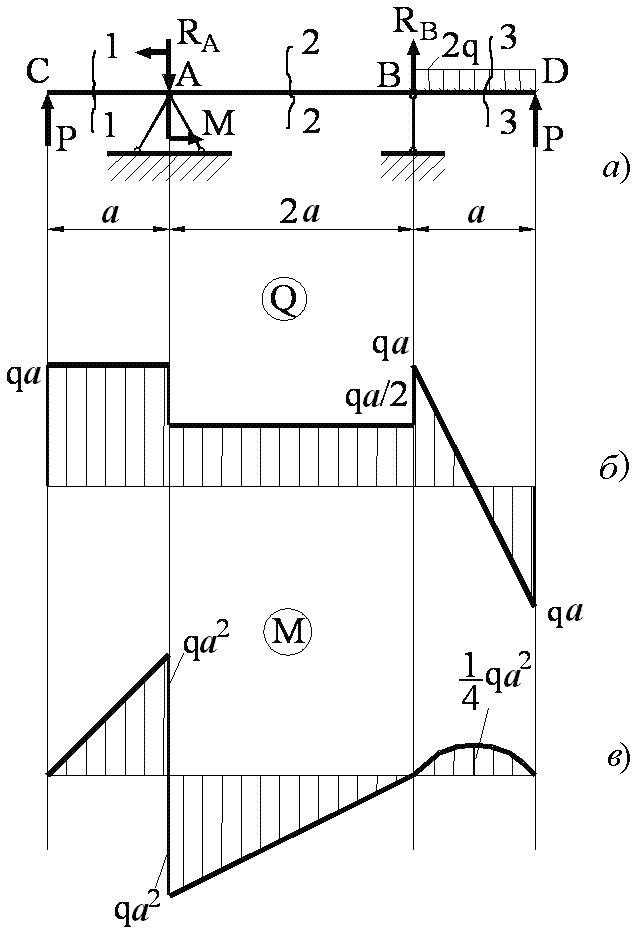
Рис. 6.1.
Решение:
1. Определение реакций опор ведем исходя из условий равновесия.
, (1)
. (2)
Решая совместно уравнения (1) и (2) получаем:
,
.
Для проверки решения рассмотрим еще одно условие равновесия:
или
.
Реакции найдены верно.
2. Построение эпюр перерезывающих сил (рис. 6.1. б) и изгибающих моментов (рис. 6.1 в).
Выделяем
три силовых участка:
,
,
.
В пределах каждого участка назначаем
переменные абсциссы
.
а) Рассмотрим
сечение 1 – 1 отстоящее на расстоянии
от точки
(рис. 6.2. а)
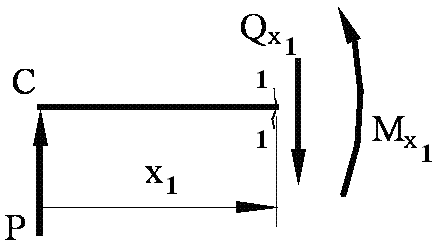
Рис. 6.2. а.
,
,
.
Сила на участке постоянна, момент изменяется по линейному закону.
Полученные аналитические значения поперечной силы и момента следует рассчитать в начальной и конечной точках каждого участка.
:
,
;
:
,
.
Строим эпюры и на первом участке.
б) Рассмотрим сечение 2 – 2. К сечению подходим слева.
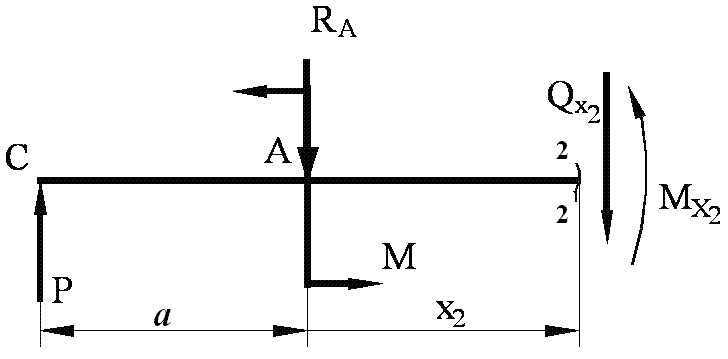
Рис. 6.2. б.
Определяем внутренние усилия в этом сечении.
: 
, 
.
При 
: 
, 
;
при 
:
, 
.
Как видим, поперечная сила на втором участке постоянна, а момент – линейная функция . Наносим полученные значения , на эпюры для второго участка.
в) Рассматриваем сечение 3 – 3. Удобнее подойти к этому сечению справа. При таком подходе знаки следует изменить на противоположные.
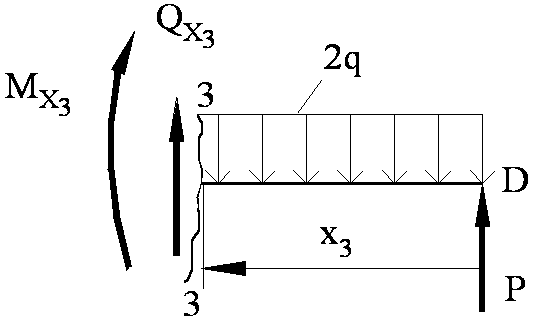
Рис. 6.2. в.
: 
, 
.
При 
: 
, 
;
при 
: 
, 
.
Поперечная сила на третьем участке изменяется по линейному закону, а функция изгибающего момента – параболическая.
Для построение
графика
необходимо провести исследование на
экстремум:
,
.
Значение
момента при
достигает экстремума:
.
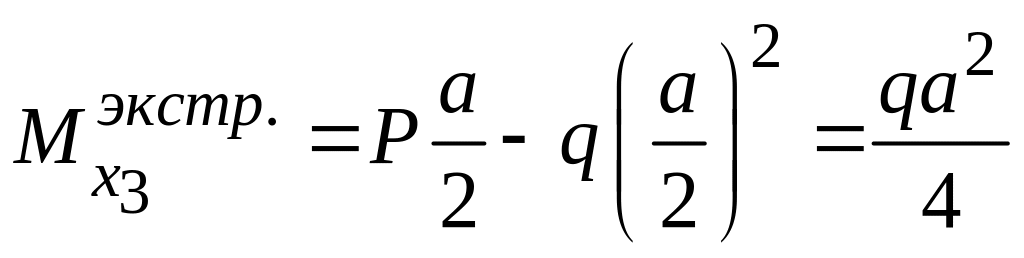Легко заметить, что при поперечная сила
,
обращается
в 0, что соответствует второй теореме
Журавского, согласно которой
Далее наносим
рассчитанные значения
и
на
эпюры
и
.
3. Определение момента сопротивления балки.
Исходя из условия прочности при изгибе по нормальным напряжениям
,
получаем необходимый для прочности момент сопротивления сечения
.
Здесь
равен значению момента в опасном сечении
балки. Опасным является сечение, где
достигает наибольшего значения по
модулю. Общие закономерности, которые
можно использовать для проверки
правильности построения эпюр
и
(значение
берут над или под осью на эпюре
).
а) На эпюре
перерезывающих сил
в тех сечениях, где на балке приложены
сосредоточенные силы, (у нас
,
,
)
наблюдается скачок (резкое изменение).
Величина и направление скачка соответствуют приложенной силе.
б) На эпюре изгибающих моментов в тех сечениях, где на балке действует сосредоточенный момент, наблюдается скачок на величину этого момента с учетом его знака.
в) В сечении,
где перерезывающая сила
изгибающий момент достигает экстремального
на этом участке значения.
г) На участке, где действует распределенная нагрузка, эпюра очерчена криволинейно, выпуклостью навстречу стрелкам нагрузки .
Задача решена.
Сложное сопротивление. Внецентренное растяжение, сжатие.
Порядок выполнения и методические указания к задаче №8:
При внецентренном
растяжении или сжатии в поперечных
сечениях бруса возникают 3 внутренних
силовых фактора: продольная сила
,
два изгибающих момента
,
относительно главных осей сечения.
Здесь
,
– координаты точки приложения нагрузки
в системе главных осей сечения.
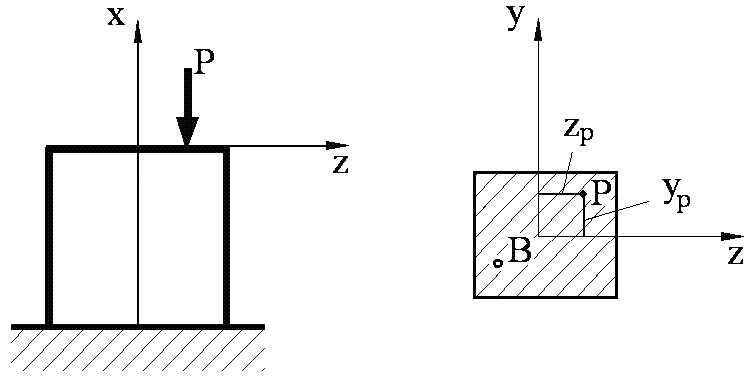
Рис. 8.1.
Напряжения
в произвольной точке
поперечного сечения с координатами
,
имеют вид:
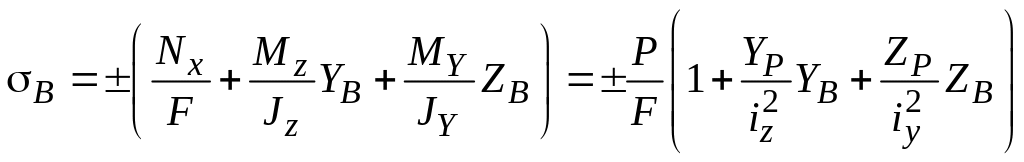, (1)
где
,
– радиусы инерции сечения.
1. Определяем
положение центра тяжести (ЦТ) заданного
сечения
,
.
Для этого следует поместить сечение в
произвольную систему координат и разбить
его на простейшие фигуры, положение ЦТ
которых легко определить.
,
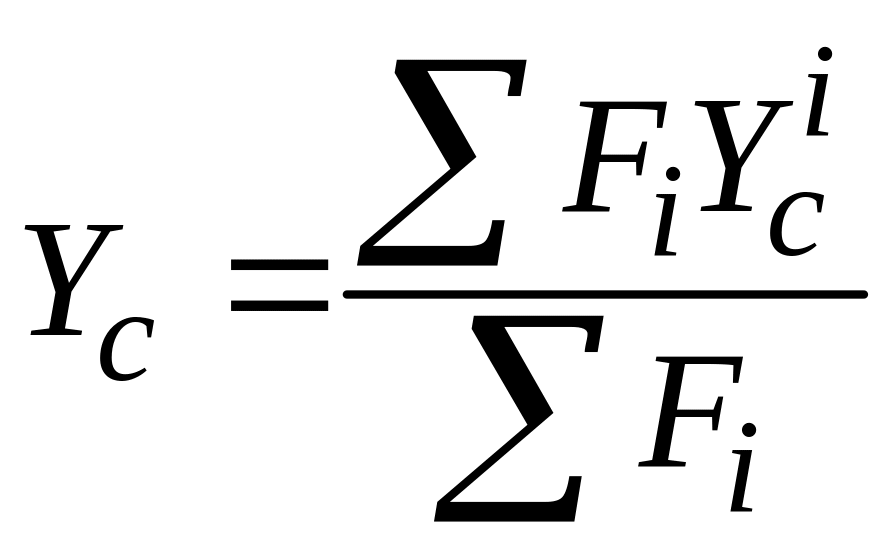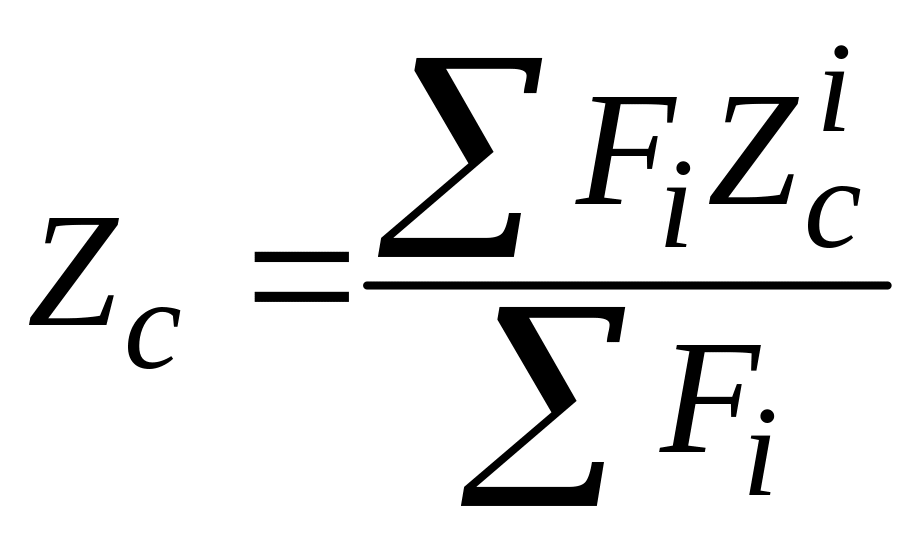(2)
здесь
– площади элементарных разбиений,
,
– координаты ЦТ разбиений.
2. Вычисляем главные центральные моменты инерции заданного сечения. Главными осями являются ось симметрии и ортогональная ей ось, проходящая через ЦТ сечения (рис. 8.2)
,
(3)
Здесь
,
– моменты инерции простых фигур
относительно собственных осей
,
,
параллельных главным осям
,
,
,
– расстояния между осями
и
,
и
соответственно.
Для удобства вычислений и проверки следует показать положение центральных осей простейших фигур и расстояния , .
3. Определяем положение нейтральной линии (НЛ). Отрезки, отсекаемые НЛ на главных осях:
,
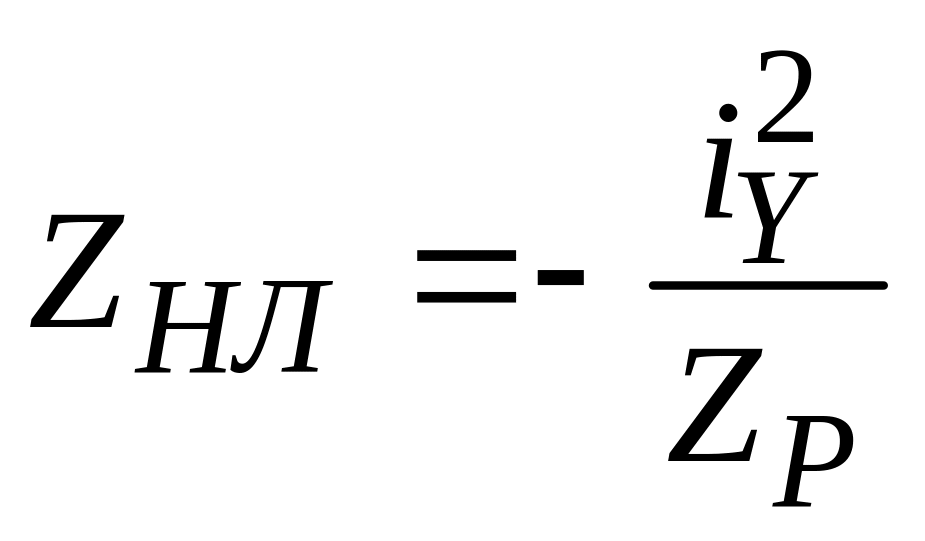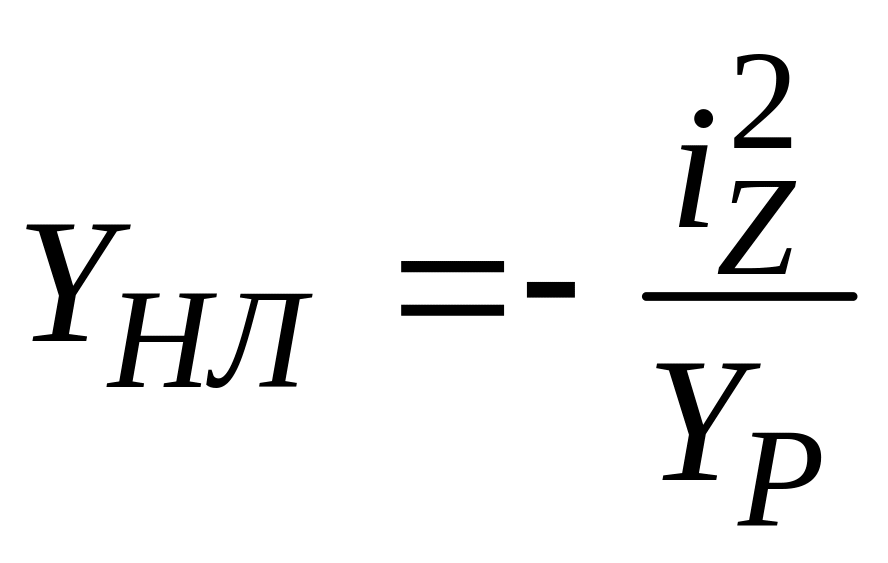. (4)
Вычислив
,
,
откладываем соответствующие отрезки
на осях
,
(рис. 8.3.) и соединяем концы отрезков
точки
и
.
Максимальные
растягивающие и сжимающие напряжения
возникают в точках наиболее удаленных
от НЛ точки
и
(рис. 8.3.)
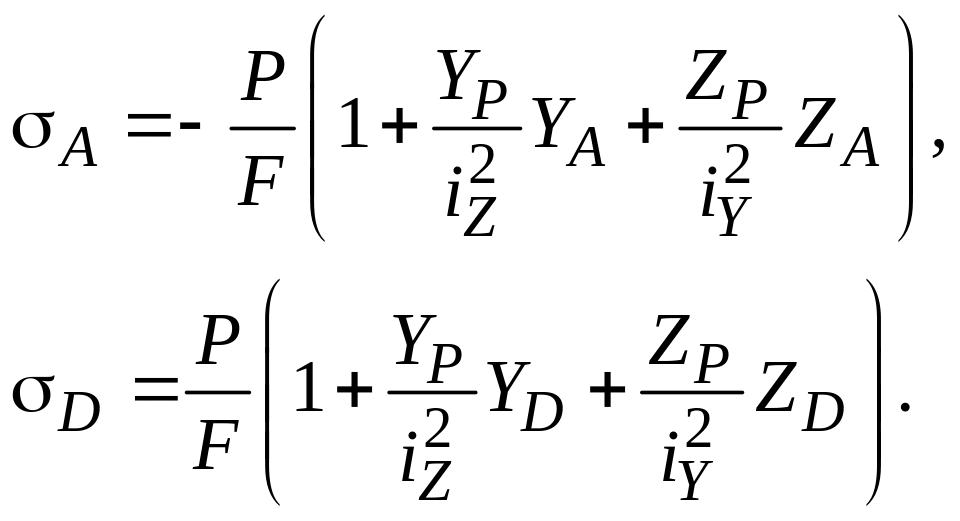(5)
Координаты
,
,
а также
,
и
,
следует брать с их знаками в системе
осей
,
.
Определяем допускаемую нагрузку с учетом:
,
.
Пример решения задачи №8
Дано сложное составное сечение (рис. 8.2.), в точке которого приложена сжимающая сила .
,
,
,
.
Найти максимальные сжимающие и растягивающие напряжения, выразив их через и допускаемое значение силы .
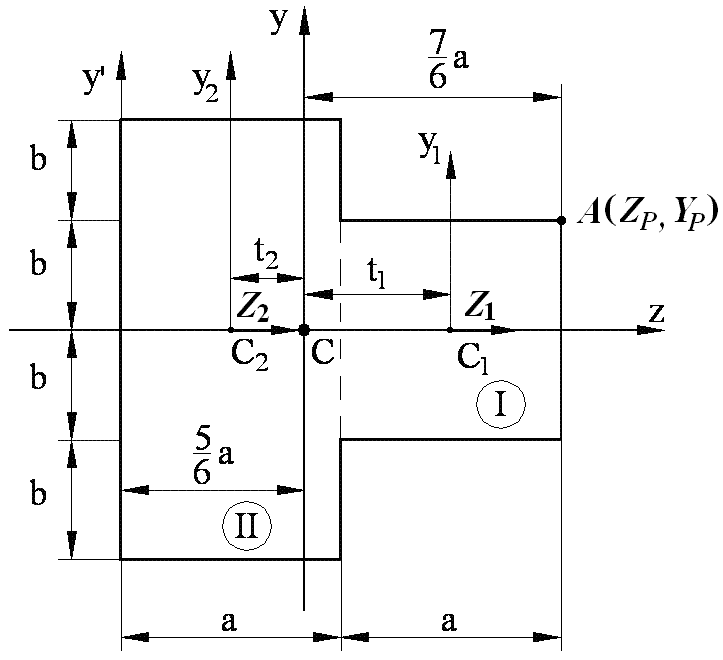
Рис. 8.2.
Решение:
1) Разбиваем сечение на (два прямоугольника) I и II.
2) Определяем
положение ЦТ составляющих сечение –
точки
,
и проводим собственные центральные оси
,
.
Собственные центральные оси
и
совпадают с осью
.
По построению имеем:
,
.
В
системе произвольно выбранных осей
координаты центров тяжести фигур I
и II.
,
,
,
.
Определяем положение ЦТ сложного составного сечения. Известно, что
,
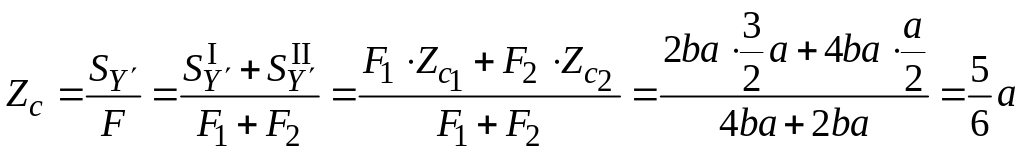(в силу симметрии
сечения).
Положение ЦТ всего сечения установлено.
3) Вычисляем главные моменты инерции сечения, используя теорему о параллельном переносе осей. Учтем, что собственные моменты инерции сечений I и II равны, соответственно:
,
,
,
.
Тогда по теореме получаем:
,
здесь
,
.
,
.
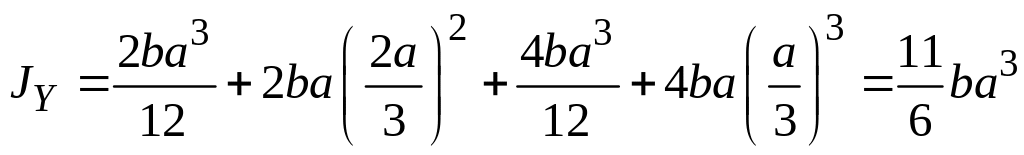4) Для определения
положения НЛ вычислим значение
,
согласно (4). Предварительно рассчитаем
и
:
,
.
Учтем,
что
,
,
,
.
Получаем:
,
.
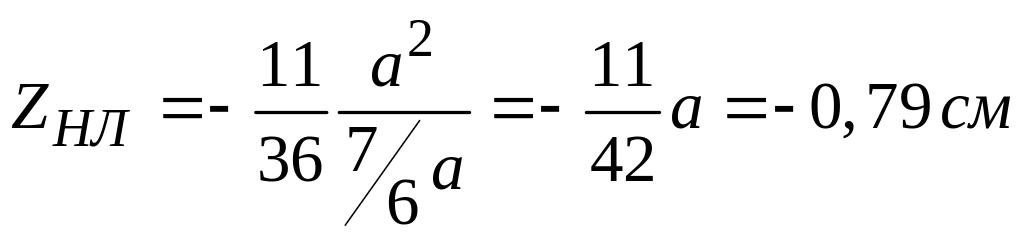5) Построение нейтральной линии, анализ распределения напряжений в сечении (рис. 8.3.):
а) откладываем
отрезки
,
с учетом их знака в системе осей
(получаем точки
и
в которых нейтральная ось пересекает
главные оси сечения);
б) соединяем точки , прямой линией. Нейтральная ось делит сечение на 2 части.
Зона, где расположена точка – зона сжимающих напряжений, противоположная – растягивающих;
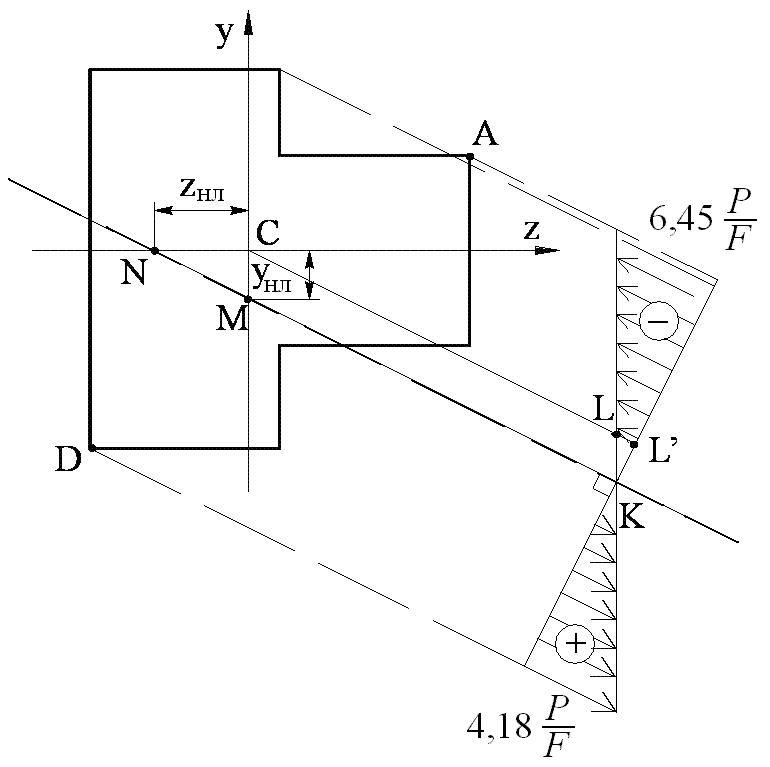
Рис. 8.3.
6) Для построения эпюры распределения напряжений в рассматриваемом сечении проводим ось перпендикулярную к нейтральной линии.
Определяем положение точек сечения, наиболее удаленных от нейтральной оси – это точки и . Через эти точки проводим линии параллельные нейтральной.
Определяем напряжение в точках и :
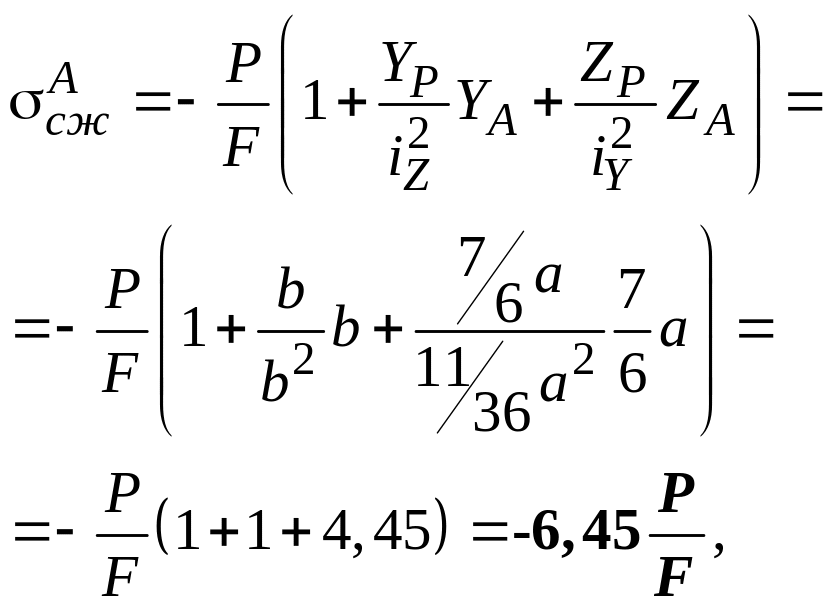
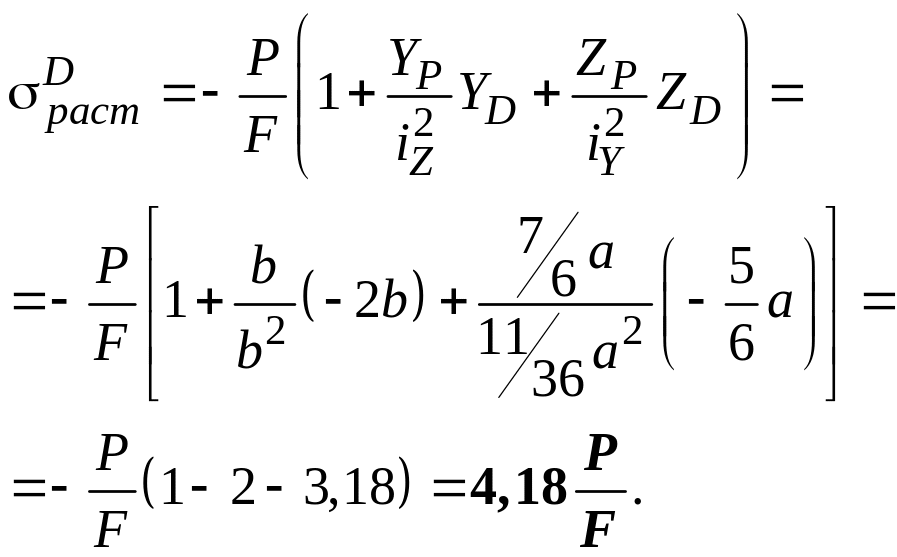
7) Определяем допускаемое значение силы
,
,
,
.
Исходя из условий прочности
,
.
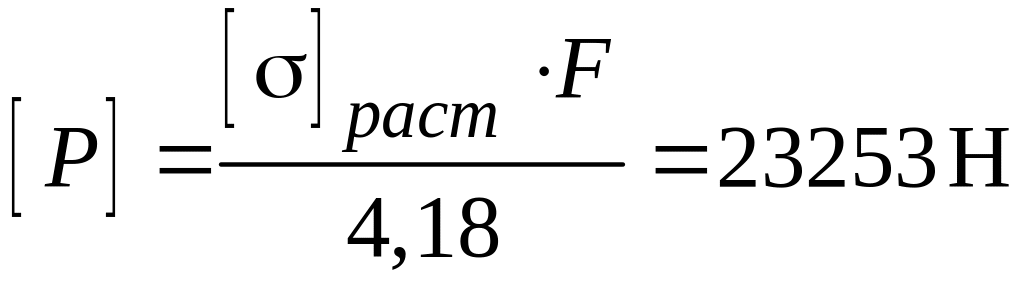Принимаем меньшее из полученных значений
.
Задача решена.