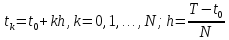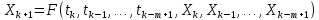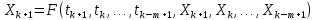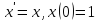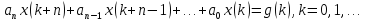- •Принципы построения, устойчивость и точность численных методов
- •Явные численные методы решения обыкновенных дифференциальных уравнений
- •Явный метод Эйлера
- •Метод Рунге – Кутта – Мерсона
- •Метод Адамса – Башфорта
- •Методы Фельберга
- •Методы Ингленда
- •Методы Нюстрема
- •Явные методы Милна
- •Явные методы Хемминга
- •Экстраполяционные методы
- •Неявные методы Милна
- •Неявные методы Хемминга
- •Методы дифференцирования назад
- •Неявные методы Рунге-Кутта
- •Описание математической модели солнечной системы и параметры ее траектории.
- •Определение и свойства моделей
- •Развитие модели Солнечной системы
- •Описание модели Солнечной системы
- •Преобразование координат в плоскости орбиты
- •Определение положения планеты на орбите в новый момент времени
- •Алгоритм прогнозирование величины радиуса
- •Алгоритм прогнозирования угла
- •Дополнительные условия
- •Вычисление декартовых координат
- •Начальные данные.
- •Вычисления и сравнения.
- •Литература
-
Принципы построения, устойчивость и точность численных методов
Пусть дана задача Коши для уравнения первого порядка
|
|
(12)
|
где X ≈ (x1, …, xn)T, X0 ≈ (x10,…, xn0)T, F(t, X)=(f1(t,X),…,fn(t,X))T. Численное решение (12) ищется на интервале [t0,T]. На этом интервале введем узлы
t0 < t1 < . . . <tk ≤ T
Приближенное решение в узлах ti ищется в виде последовательности векторов X1, X2, …, Xk приближенно равных векторам X(t1), X(t2), …, X(tk),…, определяемым точным решением X(t).
Расстояние между соседними узлами называется шагом интегрирования h: h = tk-1 – tk. Шаг может быть задан заранее (интегрирование с постоянным шагом) или может меняться в ходе вычислений. Чаще всего
|
|
(13) |
Точка Xk+1, определяется на (k+1)-й итерации, может вычисляться явно:
|
|
(14) |
где F() – некоторая функция, зависящая от конкретного алгоритма (кроме последней рассчитанной точки (tk, Xk) исползуются еще (m-1) предыдущих точек, или неявно
|
|
(15) |
Искомая величина Xk+1 входит одновременно и в левую и в правую часть. Соответственно численные методы делятся на явные и неявные.
Численные методы делятся также на одношаговые и m-шаговые. В одношаговых методах для расчета точки (tk+1, Xk+1) требуется информация только о последней рассчитанной точке (tk, Xk). В m-шаговых методах для нахождения точки (tk+1, Xk+1) требуется информация о m предыдущих точках.
Явление числовой неустойчивости связано с тем, что в течение каждой последующей итерации ошибка интегрирования неуклонно растет.
Устойчивость численных методов поверяется на «тестовом примере»:
|
|
(16) |
где - в общем случае комплексная константа. Уравнение (16) является простейшим, и любой метод, не пригодный для его решения, не представляет интереса. Линейность уравнения позволяет получить значимые критерии устойчивости в явной форме.
Метод называется устойчивым (ограниченно устойчивым), если существует такое число hkp > 0, что при использовании метода для решения задачи (16), где Re < 0, с шагом 0 < h < hkp при tk = t0 + kh ∞ глобальная ошибка ограничена. Величина hkp называется критическим шагом. Если h > hkp, глобальная ошибка может неограниченно возрастать.
Метод называется А-устойчивым, если при его применении численные решения уравнения (16) с фиксированным положительным шагом h и комплексной константой с Re < 0 стремится к нулю при tk = t0 + kh ∞.
|
Im
(h)
h
Re (h)
Рис. 1.
|
Выявление свойства А-устойчивости является желательным, так как если решение уравнения (16) асимптотически устойчиво (в силу условия h<0 корень характеристического уравнения находится в левой полуплоскости), то погрешность численного решения стремится к нулю при любой величине шага h > 0. Выбор шага определяется желаемой точностью расчетов.
Для исследования устойчивости численного метода следует использовать соответствующую разностную схему (14) или (15) для решения уравнения (16) и привести ее к линейному разностному уравнению. Критерием устойчивости решения линейного разностного уравнения с постоянными коэффициентами
|
|
Является
требование расположения корней i
соответствующего характеристического
уравнения
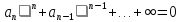 внутри
круга единичного радиуса с центром в
начале координат, то есть /i/<
1,
i
= 1, …, n.
Это условие позволяет указать область
устойчивости численного метода.
внутри
круга единичного радиуса с центром в
начале координат, то есть /i/<
1,
i
= 1, …, n.
Это условие позволяет указать область
устойчивости численного метода.
Для ограниченно устойчивых методов важной задачей является нахождение величины критического шага. Если константа в уравнении (16) действительная, то можно найти интервал устойчивости.
Существуют определения, смягчающие требование А-устойчивости, например, А()-, А(0) – устойчивости.
Задача Коши (12) называется жесткой на промежутке [t0,T], если для всех t [t0,T] выполнено:
а) Re(i) < 0, i = 1, …, n;
в)
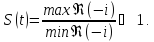
На
практике задачу можно считать жесткой,
если
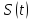 является
величиной
O
(10),
однако в некоторых прикладных областях,
коэффициент жесткости может достигать
величины O
(108).
является
величиной
O
(10),
однако в некоторых прикладных областях,
коэффициент жесткости может достигать
величины O
(108).

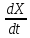 =
f (t, X), X(t0)
= X0
=
f (t, X), X(t0)
= X0