1. Розв’язати систему лінійних рівнянь за правилом Крамера.

Складемо матрицю системи рівнянь, обчислимо визначник системи та додаткові визначники:

Відповідь: х = 2 ; y = 2 ; z = 1.

2. Знайти довжину вектора , якщо відомі координати точок А(2; -1), В(-3; 0), С(5; -2).

Розв¢язання.

1. Якщо вектор має своїм початком точку А(х₁; у₁; z₁), а кінцем точку В(х₂; y₂; z₂), то кооординати вектора обчислюються за правилом:

2. Якщо то

3)Якщо то довжина . Тоді

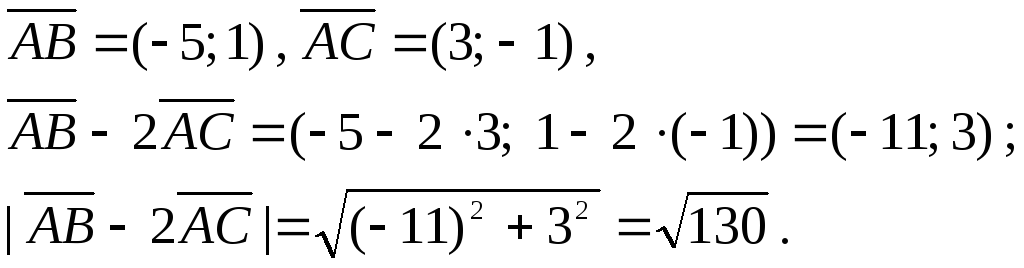
3. Знайти орт вектора

Розв’язання.

,

Тоді

Відповідь:

4. У трикутнику з вершинами А(2;-1;3), В(-2;2;5), С(1;2;3) знайти кут при вершині А.

Розв¢язання.

тоді

cosj=

j » arccos 0,763 »40°18¢.

5. Знайти точку D так, щоб чотирикутник АВСD був паралелограмом, якщо

А(-2; 0), В(1; -3), С(2; 5).

Розв¢язання.

Якщо АВСD- паралелограм, то а два вектори рівні, якщо рівні відповідні координати. Позначимо через х,у невідомі координати точки D. Тоді

З умови рівності координат маємо:

2 –х = 3, 5-у =-3, звідси х = -1, у = 8.

Отже, одержали координати точки D (-1; 8).

6. Скласти рівняння прямої, що проходить через точки М(-1; 3) та N(2; 5)

Розв’язання.

Скористаємося рівнянням прямої на площині, що проходить через точки М₁(х₁; у₁)та М₂(х₂; у₂):

.

Підставляючи в це рівняння наші дані, одержуємо

або .

Рівняння має вигляд 2х –3у +11= 0.

Корисно перевірити, що рівняння складено вірно. Для цього достатньо показати, що координати точок М та N задовольняють рівнянню прямої. Дійсно, рівності

2(-1)-3·3+11= 0, 2·2- 3·5 +11=0 виконуються тотожно.

7. Дані вершини трикутника: m(0;1); n(6;5) та с(12;-1). Скласти рівняння висоти трикутника, проведеної з вершини с.

Розв’язання.

Скористаємося рівнянням прямої на площині, яка проходить через точку C(x₀; y₀)та має вектор нормалі :

A(х-х₀) + В(у-у₀) =0.

Зі схематичного рисунка видно, що в якості вектора нормалі прямої СК можна взяти вектор . Тоді маємо:

6(x-12) + 4(у+1) =0, звідки одержуємо 3х +2у –34 =0.

8. Скласти рівняння прямої, що проходить через точку М(-2; -5) і паралельно прямій 3х +4у +2 =0.

Розв’язання.

З схематичного рисунка бачимо, що вектор нормалі даної прямої є і вектором нормалі шуканої прямої. Тоді, застосувавши рівняння з попередньої задачі, маємо:

3(х+2) + 4(у+5) =0, звідки 3х + 4у +26 =0.

9. Дані вершини трикутника А(-2; -3), В(5; 4) та С(-1; 2). Скласти рівняння медіани АМ.

Розв’язання.

Точка М –середина сторони ВС, тому

.

Використовуючи рівняння прямої, що проходить через точки А і М, знаходимо рівняння медіани АМ:

звідки 3х-2у=0.

10. Провести серединний перпендикуляр відрізка ав, де а(0; -2), в(4; 0).

Розв’язання.

Маємо С(2; -1). Розглядаючи як вектор нормалі шуканої прямої, маємо: 4(х-2) +2(у+1) =0, звідки 2х + у –2 =0.

11. Дані рівняння сторін трикутника:

х + 3у –7= 0 (АВ), 4х –у- 2= 0 (ВС),6х +8у –35= 0 (АС).

Знайти довжину висоти, проведеної з вершини В.

Розв’язання.

Визначимо координати точки В. Розв’язуючи систему рівнянь

х + 3у –7= 0 та 4х –у- 2= 0, одержимо х=1,у= 2, тобто В(1;2). Скористаємося формулою для обчислення відстані від

точки М₀( х₀;у₀)до прямої Ах +Ву + С =0:

Знаходимо довжину висоти ВВ₁ як відстань від точки В до прямої АС:

12. Знайти проекцію точки р(4;9)на пряму, що проходить через точки а(3; 1) та в(5; 4).

Розв’язання.

Проекція точки на пряму- це основа перпендикуляра, опущеного з точки на пряму. Для її одержання достатньо розв”язати сумісно рівняння прямої АВ і прямої, що проходить через точку Р перпендикулярно АВ.

Рівняння АВ запишемо, скориставшись рівнянням

де та - відомі точки прямої.

Тоді або .

Рівняння другої прямої запишемо, скориставшись рівнянням

де - вектор нормалі прямої, а

- точка прямої.

Вибравши в якості нормального вектора напрямний вектор прямої АВ, маємо:

2(х-4) +3(у-9)=0.

Таким чином:

Розв’язавши цю систему, одержимо: х = 7, у = 7.

Отже, проекція точки Р на задану пряму - точка С(7, 7).

13. Скласти рівняння площини, яка проходить через точку м0(2;3;5) і перпендикулярно вектору .

Розв’язання.

Достатньо скористатися рівнянням площини, яка проходить через дану точку М₀(x₀;y₀;z₀) і має вектор нормалі :

.

Тоді у нашому випадку маємо:

4(х-2)+3(у-3)+2(z-5)=0, звідси одержуємо рівняння шуканої площини:

4х +3у +2z –27 =0.

14. Написати рівняння площини, що проходить через точку М₀(2; 3; -1) паралельно площині 5х – у + 3z = 5.

Розв’язання.

Скориставшись рівнянням площини, що проходить через задану точку, запишемо А(х-2)+В(у-3)+С(z+1)=0. З паралельності площин випливає, що шукана площина має нормальний вектор

, тому рівняння шуканої площини має вигляд

5(х-2) –(у-3) +3(z+1) = 0, або 5х – у + 3z – 4 = 0.