Тема 13. Перевірка статистичних гіпотез

Сг- гіпотеза про вид невідомого розподілу, значення відомого розподілу, незалежність вибірок тощо.

Розрізняють параметричні і непараметричні, прості і складені статистичні гіпотези. Параметричні стосуються значень параметрів, непараметричні – решта. Розрізняють основну (нульову) Но і альтернативну їй гіпотезу Н1

Но: Mξ=а – проста гіпотеза

Н1: Mξ ≥≤≠а – складна

Якщо при перевірці Но результати вибірки суперечать тому, що стверджує Но, то Но відхиляється, а інакше приймається. При цьому можливі помилки 2х типів:

1) помилка 1го роду: Но відхиляється коли дана гіпотеза вірна. Ймовірність такої помилки називається рівнем значущості (α).

2) Помилка 2го роду : Но прийняли коли Н1 вірно. Ймовірність такої помилки (β)

1-β називається потужністю критерію перевірки Но.

Критерієм перевірки Но (статистики) називається ВВ, що побудована, що побудована за вибіркою і використовується для перевірки Но.

Потужність критерію (1-β) – це ймовірність Но, коли Но не вірне.

Критерій згоди – це статистичні критерії, що дозволяють перевірити гіпотезу про вид закону розподілу ГС.

Но: ознака ГС має певний теоретичний закон розподілу

Н1: ознака ГС має інший закон розподілу

Критерій Пірсона перевірки Но:

n – об’єм вибірки

mi – частоти варіант вибірки або частинних унтервалів.

Рі – теоретична ймовірність, що відповідає варіанті вибірки або частинному інтервалу вибірки

k – кількість різних варіант вибірки

Доведено, що статистичнийтарозподіл з s=k-1-r ступенями свободи. r – кількість параметрів ГС, що оцінюються за вибіркою.

Зауваження:

1.Но: ознака ГС має розподіл Пуассона,

-точкова оцінка

………………….

i = 0,1,2

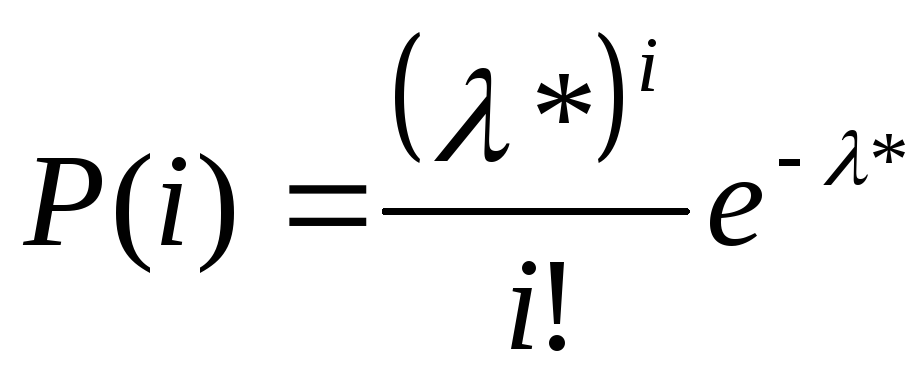
2. Но: ознака ГС має нормальний закон розподілу

; ;

;

Гіпотеза однорідності. Нехай маємо k вибірок z=( x

1, x

2, …, x

n), i = 1, k з генеральних

сукупностей з функціями розподілу Fi (x ), i = 1, k. Потрібно перевірити гіпотезу про те, що це

спостереження над однією і тією ж випадковою величиною, тобто H 0 : F1 (x ) º F2 (x ) ºKº Fk (x ).

3. Гіпотеза незалежності. Одночасно спостерігаються дві випадкові величини x та h, F(x ,h )(x, y)

— невідома їхня сумісна функція розподілу. Потрібно перевірити гіпотезу про те, що x та h — незалежні

випадкові величини, тобто H 0 : F(x ,h )(x, y) = Fx (x )Fh (y).

Тема 14.

1. Перевірка гіпотез про рівність дисперсій нормальних ознак гс (ознаки мають норм розподіл).

Нехай розглядається ознака ξ з розподілами N() та η N(), де і - невідомі. Нехай є вибірки з ГС: ξ: η:.

Статистика для перевірки : ;

Відомо,що статистика S має розподіл Фішера з ступенями свободи, де , . Будується правобічна критична область за допом визначення критичної точки: - табл. Розпад Фішера (

Якщо (приймається); (відхиляється)

2. Перевірка гіпотез про рівність матем сподівань нормальних ознак ГС при відомих дисперсіях.

Нехай розглядається ознака ξ з розподілами N() та η N(), де -невідомі, а - відомі. Нехай є вибірки з ГС: ξ: η:.

Статистика для перевірки :

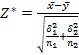
Відомо,що статистика Z має норм розподіл N(0,1). Критичну точку шукають як розв’язок рів-ня: Ф( (ф-ція Лапласа табл. 2)

Якщо (приймається); (відхиляється)

3. Перевірка гіпотез про рівність мат сподівань норм розподілених ознак ГС при невідомих,але рівних дисперсіях.

Нехай розглядається ознака ξ з розподілами N() та η N(), де і – невідомі,але доведено що . Маємо незал вибірки з ГС: ξ: η:

Статистика для перевірки : ;

Відомо,що статистика T має розподіл Стюдента з k ступенями свободи, де . Будується двобічна критична область. Критичну точку беремо з табл розп Стюдента,де: ( k- вище

Якщо (приймається); (відхиляється)

3. Перевірка гіпотез про рівність дисперсій, при відомих математичних сподіваннях (а)

Ця гіп0теза анал0гічна I., але в дан0му випадку , де

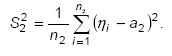
Якш0 правильна гіп0теза т0 випадк0ва величина F має р0зп0діл Фішера-Снедек0ра з (n1,n2) степенями св0б0ди. Критична мн0жина задається нерівністю: