4. Анализ систем управления

При управлении системами ставятся следующие цели:

• точность – в установившемся режиме система должна поддерживать заданное значение входа, причем ошибка (разница между заданным и фактическим значением) не должна превышать допустимую величину;

• устойчивость – система должна оставаться устойчивой во всех режимах;

• качество переходных процессов - при смене заданного значения система должна переходить в нужное состояние по возможности быстро и плавно;

• робастность – система должна сохранять устойчивость и приемлимое качество даже в том случае, если динамика объекта и свойства внешних возмущений отличаются от используемых при проектировании.

4.1. Точность

Точность системы обычно оценивается для одного из эталонных сигналов:

Единичный скачок

Линейно-возрастающий сигнал

Гармонический сигнал

Точность системы в установившемся режиме определяется ошибкой e(t) или ее изображением E(s). Для исследования точности используют передаточную функцию по ошибке W_e(s), которая связывает изображения ошибки и входного сигнала:

регулятор объект

Х

e u y

(-)

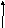
E(s) = W_e(s) * X(s)

Разложим функцию W_e(s) в ряд, получим:

где: . . .

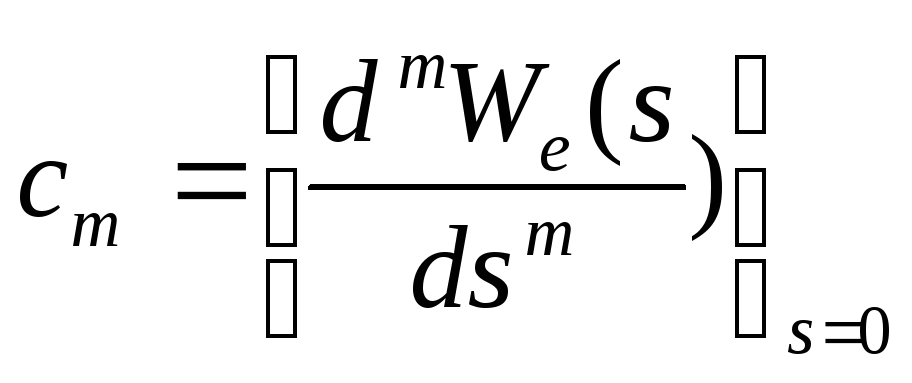
Представим передаточные функции C(s) и P(s), изображение входа X(s) в виде отношения полиномов:

С учетом этого передаточная функция по ошибке из представленной схемы равна:

где: Δ(s) = d_c(s) d(s) + n_c(s) n(s) – характеристический полином замкнутой системы.

Рассмотрим реакцию системы на единичный ступенчатый сигнал, изображение которого равно:

Сигнал ошибки определяется полюсами передаточной функции W_e(s) (корнями Δ(s) и полюсами изображения X(s)).

Все полюса W_e(s) должны иметь отрицательные вещественные части (иначе система будет неустойчивой), нулевых полюсов у функции W_e(s) тоже нет. Тогда [1]:

где: Y₀(s) – полюса только с отрицательной вещественной частью;

Для того чтобы сделать нулевую ошибку достаточно обеспечить:

d_c(0) = 0 регулятор содержит интегратор;

d(0) = 0 объект содержит интегратор.

Таким образом, для любых незатухающих входных сигналов ошибка стремится к нулю в том случае, если их полюса сократились в произведении:

Это возможно только тогда, когда они являются корнями полинома d_c(s)d(s).

Например, для точного отслеживания ступенчатого сигнала нужно, чтобы объект или регулятор содержали интегрирующее звено (с передаточной функцией 1/s). Тогда произведение d_c(s)d(s) имеет сомножитель s и полюс X(s) в точке s=0 сократится в произведении W_e(s) X(s).

Таким образом, если передаточная функция разомкнутого контура C(s)P(s) содержит множитель s в знаменателе, обеспечивается нулевая ошибка слежения за постоянным сигналом (нулевая статическая ошибка). Такая система называется астатической. Для отслеживания линейно возрастающего сигнала в таком контуре должно уже быть два интегратора (нужно сократить двойной полюс X(s) в точке s=0). Такая система обладает астатизмом 2-го порядка.

В общем случае система, в которой:

где: ν > 0 натуральное число; функция G(s) не имеет нулей и полюсов в точке s=0;

называется астатической системой ν-го порядка.

Такая система в установившемся режиме без ошибки отслеживает сигнал вида:

при любыхx_i (i=0, 1, …, ν-1).

Казалось бы, для повышения точности системы можно поставить множество интеграторов и проблемы воспроизведения без ошибки входного сигнала любого вида будут решены. Однако добавление каждого нового интегратора в систему ухудшает качество переходных процессов, осложняет стабилизацию системы, снижает ее быстродействие.

4.2. Повышение точности систем управления

Известны следующие общие методы повышения точности систем [1]:

1. Увеличение коэффициента передачи разомкнутой системы.

2. Повышение порядка астатизма.

3. Управление производными по ошибке

Первый метод является наиболее универсальным и эффективным: как результат его применения является уменьшение ошибок практически во всех режимах. Однако увеличение коэффициента передачи ограничивается устойчивостью системы. При повышении коэффициента передачи переходные процессы в системе приобретают колебательный характер, при предельном значении возникают незатухающие колебания. На практике повышение коэффициента передачи обычно производится только при повышении запаса устойчивости системы, что осуществляется при помощи корректирующих средств (звеньев).

Второй метод используется для устранения установившихся ошибок в различных типовых режимах (введением интегрирующих звеньев) [1]:

g

x y

(-)

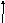Пример

введем интегрирующее звено, получим:

Характеристический полином замкнутой системы равен:

Т₁Т₂s⁴ + (Т₁+Т₂)s³ + s² + К*К_и

Как видно, при s слагаемое в полиноме отсутствует (т.е. а₃ = 0), значит, система структурно неустойчива, необходимо изменить структуру системы только при помощи корректирующих средств.

Кроме интегрирующих звеньев в этом методе используется введение изодромных устройств.

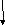
g x y

(-)

Вернемся к предыдущему примеру. Передаточная функция разомкнутой системы в случае введения изодромного звена равна:

Характеристический полином замкнутой системы равен:

Т₁Т₂s⁴ + (Т₁+Т₂)s³ + s² + К*К_иТ_иs + К*К_и

Коэффициенты ошибок равны:

с₀ = с₁ = 0

Третий метод повышения точности – управление производными по ошибке – заключается в ведении дифференцирующего элемента:

g x y

(-)

Введение дифференцирующего элемента не влияет на первый, отличный от нуля, коэффициент ошибки, но зато уменьшает последующие коэффициенты [1].

На практике наиболее эффективное снижение ошибки в системе заключается в одновременном использовании изодромных (не более трех) и дифференцирующих (не более двух) элементов.

4.3. Анализ устойчивости линейных непрерывных систем управления

Понятие устойчивости является особенно важным, поскольку данное свойство системы определяет факт ее работоспособности или неработоспособности.

Линейные системы управления обладают особенностями, которые во многих случаях упрощают анализ устойчивости:

• устойчивость - это свойство линейной системы, а не отдельного положения равновесия: или все движения системы устойчивы, или все движения неустойчивы;

• устойчивость линейной системы не зависит от вида и характера изменения задающего и возмущающих воздействий.

Для того, чтобы получить условия устойчивости рассмотрим уравнение движения линейной системы, на которую не действуют возмущения. передаточная функция системы имеет следующий вид:

где: n(s), Δ (s) - полиномы; α_i (i=1,...n) - простые (некратные) полюса (корни знаменателя).

Из теории дифференциальных уравнений известно, что при отсутствии возмущений выход такой системы можно представить в виде:

где: α_i (i=1,...n) - постоянные, определяющиеся начальными условиями.

Процесс y(t) затухает при любых начальных условиях тогда и только тогда, когда все корни α_i имеют отрицательные вещественные части. В этом случае система асимптотически устойчива [1].

Таким образом, устойчивость линейной системы управления определяют корни полинома Δ (s) - знаменателя передаточной функции. Этот полином называется характеристическим полиномом системы.

Так как все коэффициенты полинома Δ (s) вещественные, комплексные корни всегда будут парными.

Если один из корней α_i полинома Δ (s) равен нулю, а остальные корни устойчивы, это значит, что система содержит интегрирующее звено: при всехt, получаем:

здесь все слагаемые затухают с течением времени, а постоянная составляющая α_i остается, в этом случае система нейтрально устойчива.

Если характеристический полином имеет пару чисто мнимых корней: α₁= jω α₂= - jω, то система содержит консервативное звено (генератор колебаний). На выходе получится:

Эти составляющие дают незатухающие колебания, система в этом случае нейтрально устойчива.

Если в характеристическом полиноме имеется хотя бы один корень с положительной вещественной частью, то система неустойчива.

Критерии устойчивости

На практике обычно пользуются критериями устойчивости - правилами, позволяющими оценить устойчивость без вычисления корней.

Критерии устойчивости классифицируют на алгебраические и частотные. Алгебраические критерии позволяют определить устойчивость системы при помощи только алгебраических процедур над коэффициентами характеристического уравнения. К ним относятся критерии устойчивости Рауса, Гурвица и другие. Частотный критерий устойчивости, впервые сформулированный Найквистом, был применен для устойчивости систем управления А.В. Михайловым. Кроме того, последний сформулировал другой частотный критерий, названный его именем. Достоинством частотных критериев является их наглядность, а также возможность использовать частотные характеристики, полученные экспериментально, когда неизвестны дифференциальные уравнения системы или его элементов.

Наибольшее распространение получил алгебраический критерий устойчивости, сформулированный Гурвицем.

Для характеристического полинома (уравнения) системы:

составим квадратную матрицу H_n, содержащую n строк и n столбцов.

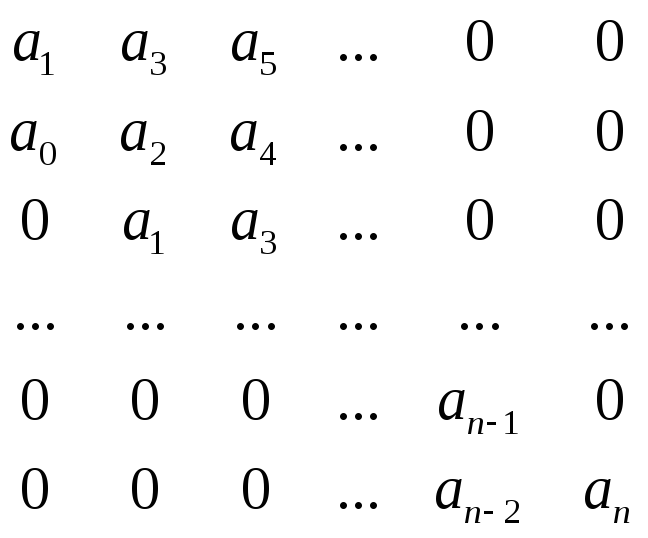
Первая строка содержит коэффициенты с нечетными номерами (a₁,a₃,a₅,....) - оставшиеся элементы матрицы заполняются нулями.

Вторая строка содержит коэффициенты с четными номерами (a₀,a₂,a₄,....) - оставшиеся элементы матрицы заполняются нулями.

Третья и четвертая строки получаются сдвигом первой и второй строк на одну позицию вправо и т.д.

Например, для системы пятого порядка такая матрица H₅ имеет вид:

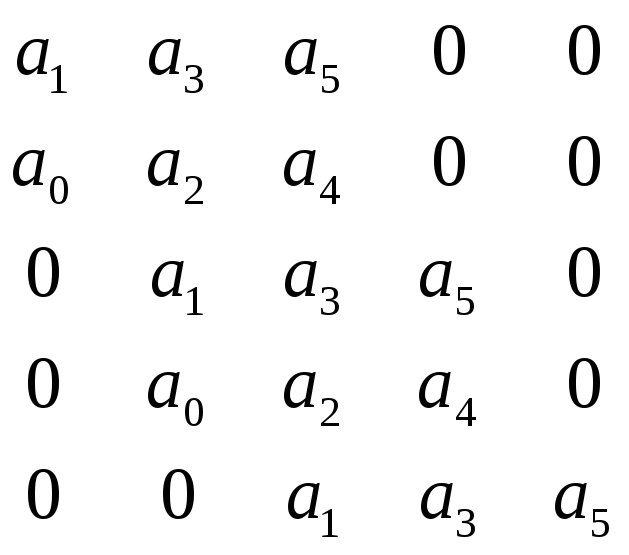
Критерий Гурвица: все корни полинома Δ (s) имеют отрицательные вещественные части тогда и только тогда, когда все n главных миноров матрицы H_n (определителей Гурвица) положительны: Δ _n = a_n Δ_n-1 > 0.

Система находится на границе устойчивости, когда Δ _n = 0:

при a_n =0 - апериодическая граница устойчивости;

при Δ_n-1=0 - колебательная граница устойчивости.

Определители Гурвица составляются по следующему правилу:

Δ₁ = a₁ > 0

Δ₂ = > 0

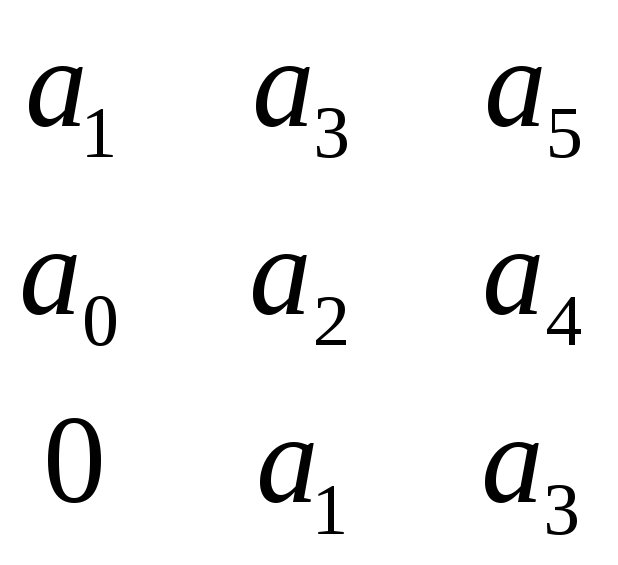Δ₃ = > 0

Раскрывая определители, фигурирующие в общей формулировке критерия, можно получить в виде частных случаев критерии устойчивости для систем: 1-го, 2-го, 3-го и более высоких порядков.

Для систем 1-го порядка: a₀ s + a₁ ; a₀ >0 Δ₁ = a₁ > 0

Для систем 2-го порядка: a₀ s² +a₁ s + a₂ ; a₀ >0 Δ₁ = a₁ > 0 Δ₂ = a₁a₂ > 0 a₂ > 0

Для систем 3-го порядка: a₀ s³ +a₁ s² + a₂ s +a₃ ; a₀ > 0 a₁ > 0 a₂ > 0

Δ₃ = a₃ > 0 a₃ >0 > 0

a₁ a₂ - a₃ a₀ >0 a₁ a₂ > a₃ a₀

Как видно, помимо положительности всех коэффициентов характеристического полинома с ростом порядка системы возникают другие условия.

Как правило, использование критерия Гурвица ограничивается уравнениями четвертого порядка.

Критерий Гурвица не дает для высоких порядков характеристического уравнения ответа на вопрос, каким образом надо изменять параметры системы, чтобы она была устойчивой.

Пример

регулятор объект

Х

e u y

(-)

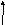
При каких значениях К система будет устойчивой по критерию Гурвица?

Δ(s) = Т₁Т₂s³ + (Т₁+Т₂)s² + s + К

Условия устойчивости:

К > 0 ; Т₁*Т₂ > 0 ; Т₁+Т₂ > 0

(Т₁+Т₂) * 1 > К * Т₁Т₂

Отсюда:

С учетом того, что постоянные времени Т1 и Т2 всегда больше нуля, система устойчива при следующих значениях К:

Критерий Найквиста

Это графоаналитический критерий, в котором вывод об устойчивости или неустойчивости замкнутой системы делается в зависимости от вида частотной характеристики разомкнутой системы. Кроме того, при помощи этого критерия можно оценить качественные показатели замкнутой системы (например, запас устойчивости). Критерий Найквиста позволяет определить устойчивость замкнутой системы, построив частотную характеристику разомкнутой системы:

Х

L(s)

e y

(-)

L(s) – передаточная функция разомкнутой системы;

L(jω) – частотная характеристика разомкнутой системы.

Для каждой частоты ω значение L(jω) – это комплексное число, которое можно изобразить на комплексной плоскости. При изменении частоты от 0 до ∞, из этих точек складывается годограф Найквиста – кривая, начинающаяся при значении L(0) и заканчивающаяся в начале координат (так как L(s) – строго правильная функция, степень числителя меньше степени знаменателя).

Система устойчива тогда и только тогда, когда годограф не охватывает точку (-1,0).

Система находится на границе устойчивости, если частотная характеристика проходит через точку (-1,0). В этом случае, для некоторой частоты ω имеем: А(ω)=1 ; φ(ω) = -180⁰. Это говорит о том, что сигнал меняет знак, сохраняя величину, т.е. возникают незатухающие колебания.

Частота ω, дл которой А(ω)=1 называется частотой среза.

Для устойчивой системы значение фазы при частоте среза должно быть больше -180⁰, в этом случае годограф не охватит точку (-1,0).

Если передаточная функция L(s) имеет полюса в точке s = 0, то годограф начинается не на вещественной оси, а приходит из бесконечности. Тогда в годограф необходимо включить не только полученную кривую, но и часть окружности бесконечного радиуса от вещественной оси до годографа в порядке обхода по часовой стрелке. Если функция L(s) имеет К полюсов в точке s = 0, нужно добавить К секторов по 90⁰.

Если в системе имеется запаздывание на время τ, то на любой частоте появляется дополнительный сдвиг фазы на – τω без изменения амплитуды. Это значит, что каждая точка годографа поворачивается на некоторый угол против часовой стрелки. Таким образом, запаздывание всегда ухудшает устойчивость системы.

Если передаточная функция L(s) имеет полюса с положительной вещественной частью (разомкнутая система неустойчива), нужно считать сколько раз годограф пересекает ось абцисс левее точки (-1,0), при этом: пересечение оси сверху вниз считает за положительный переход, а пересечение оси снизу вверх - за отрицательный переход.

Для того, чтобы замкнутая система была устойчива необходимо и достаточно, чтобы разница между числом положительных и отрицательных переходов была равна l / 2 , где: l – число неустойчивых полюсов функции L(s). Начальная точка годографа на оси абцисс левее точки (-1,0) считается за половину перехода.

4.4. Переходный процесс.

Спроектированная система должна не только быть устойчивой и поддерживать заданную точность в установившемся режиме, но и плавно переходить на новый режим при изменении входного воздействия.

Качество переходных процессов обычно оценивается по переходной характеристике (реакции системы на единичный ступенчатый входной сигнал).

В первую очередь, интересует насколько быстро заканчивается переход на другой режим (время переходного процесса - время регулирования - tрег). Эта величина определяется как время, через которое регулируемая величина "входит в коридор" 2Δ вокруг установившегося значения y_∞ . Это значит, при времени t > tрег значение выхода отличается от установившегося не более, чем на Δ. Обычно величина Δ составляет от 2% до 5 % от установившегося выходного значения.

Другая характеристика переходного процесса (перерегулирование σ) показывает, насколько процентов максимальное значение выхода y_max превышает установившееся значение y_∞ (или минимальное значение y_min ниже установившегося значения y_∞):

Иногда удается обеспечить нулевое перерегулирование (апериодический переходный процесс). Необходимо помнить, что увеличение быстродействия (уменьшение tрег) обычно приводит к увеличению величины перерегулирования.

Как известно, устойчивость линейной системы определяется полюсами передаточной функции, однако на вид переходного процесса влияют и нули передаточной функции, в некоторых случаях очень существенно [1].

Пример.

В этом случае ноль передаточной функции равен: s = - 1 / а .

При a > 0 σ > 0 при a < 0 σ < 0, при a = 0 переходный процесс имеет вид апериодического звена второго порядка. Чем больше |а|, тем больше величина перерегулирования σ.

Частотные оценки качества

Из частотных оценок качества наиболее важными являются запасы устойчивости (по амплитуде и по фазе).

Запас устойчивости по амплитуде g_m измеряется в децибелах и показывает дополнительное усиление контура, необходимое для вывода системы на границу устойчивости (при проектировании систем должен составлять не менее 6 дБ), определяется следующим образом:

где: A_g – значение амплитудной характеристики, где значение фазы фаза равна -180⁰.

Запас устойчивости по фазе измеряется в градусах и показывает дополнительный сдвиг фазы, необходимый для вывода системы на границу устойчивости (при проектировании систем должен составлять не менее 30⁰).

Еще одной частотной оценкой качества системы является показатель колебательности. Показатель колебательности М определяется по амплитудно-частотной характеристике замкнутой системы как отношение ее максимума к значению на нулевой частоте (чем меньше значение этого показателя, тем лучший вид имеет переходный процесс в системе):

Корневые оценки качества

Многие свойства системы можно предсказать, исходя из расположения корней характеристического уравнения Δ(s) на комплексной плоскости. Для устойчивости системы все корни Δ(s) должны находиться в левой полуплоскости, т.е. слева от мнимой оси.

Быстродействие системы определяется степенью устойчивости η – расстоянием от мнимой оси до ближайшего корня или пары комплексно-сопряженных корней. Этот корень определяет самые медленные движения в системе:

Степень устойчивости η характеризует быстродействие, эта характеристика ничего не говорит о близости системы к границе устойчивости.

Колебательность μ – параметр, определяющий скорость затухания колебаний в системе (в случае наличия пары комплексно-сопряженных корней: α ± β):

Чем больше величина колебательности μ, тем слабее затухают колебания в системе.

На практике при проектировании системы обычно требуется обеспечить колебательность не выше заданной μ_max и быстродействие не ниже заданного (степень устойчивости не менее η_min).

4.5. Робастность

При построении систему управления требуется, чтобы регулятор обеспечивал устойчивость и приемлимое качество системы при небольших отклонениях свойств объекта и внешних возмущений от номинальных значений. Это свойство называется робастностью (грубостью). Иначе говор, это нечувствительность к малым ошибкам моделирования объекта и возмущений.

Различают следующие задачи, связанные с робастностью:

• робастная устойчивость (обеспечение устойчивости системы при всех допустимых отклонениях модели объекта от номинальной);

• робастное качество (обеспечение устойчивости и заданных показателей качества системы при всех допустимых отклонениях модели объекта от номинальной);

• гарантирующее управление (обеспечение заданных показателей качества системы при всех допустимых отклонениях модели возмущения от номинальной, при этом модель объекта известна точно).

Для того, чтобы исследовать робастность системы, требуется определить возможную ошибку моделирования (неопределенность). Эту ошибку можно задать различными способами.

Параметрическая неопределенность

Параметрическая неопределенность означает, что структура модели известна, а параметры могут отличаться от номинальных значений.

Пример.

Передаточная функция объекта равна:

где: ε₁, ε₂ – малые ошибки моделирования; К₀, Т₀ – номинальные значения коэффициента усиления и постоянной времени.

Пусть такой объект управляется регулятором-усилителем с передаточной функцией:

Тогда характеристический полином замкнутой системы имеет вид:

Δ(s) = (Т₀+ε₂)s + 1 + К(К₀+ε₁)

Условия устойчивости:

Т₀ + ε₂ > 0 1+ К(К₀+ε₁) > 0

Будем считать, что Т₀ > 0 и К₀ > 0 и отклонения ε₁ и ε₂ малы по сравнению с К₀ и Т₀ соответственно.

Т₀ + ε₂ > 0 при всех возможных ε₂.

Замкнутая система устойчива при:

1+ К(К₀+ε₁) > 0

Отсюда:

Наибольшее значение правой части неравенства будет при максимальном значении ε₁, поэтому условие робастности:

Таким образом, регулятор-усилитель при K > K_min обеспечивает робастную устойчивость системы при всех допустимых значениях ε₁ и ε₂.

Непараметрическая неопределенность

Непараметрическая неопределенность задает допустимую ошибку в частотной области (ошибку в частотных характеристиках).

Для номинальной модели P₀(jω) различают аддитивную неопределенность (абсолютную ошибку Δ_а(jω)):

P(jω) = P₀(jω) + Δ_а(jω)

И мультипликативную неопределенность (относительную ошибку Δ_m(jω)):

P(jω) = [1+ Δ_m(jω)] P₀(jω)

Для мультипликативной неопределенности известен критерий робастной устойчивости: система с регулятором C(s) и номинальным объектом P₀(s) робастно устойчива, если для любой частоты выполняется неравенство:

|W₀(jω) * Δ_m(jω)| < 1

где: W₀(s) – передаточная функция номинальной замкнутой системы:

Обычно модель системы строится так, чтобы хорошо описывать свойства реального объекта на низких частотах, для высоких частот ошибка Δ_m(jω) может быть значительной. Для робастной устойчивости значение |W₀(jω)| должно быть мало на высоких частотах, где велика неопределенность модели.

4.6. Улучшение качества процесса управления

Под улучшением качества процесса управления, кроме повышения точности, понимается изменение динамических свойств системы с целью получения необходимого запаса устойчивости и быстродействия.

При решении этой задачи сначала изменяют параметры системы (коэффициенты передачи отдельных звеньев, постоянные времени и др.), а затем изменяют ее структуру. При изменении структуры в систему вводятся корректирующие средства, изменяющие динамику всей системы. К корректирующим средствам относятся корректирующие звенья (динамические звенья с определенными передаточными функциями). Корректирующие звенья могут вводиться в систему различными способами.

Последовательные корректирующие звенья

Х₁ X₂ X₃

где: W_c(s) – передаточная функция исходной системы; W_к1(s) – передаточная функция корректирующего звена.

Параллельные корректирующие звенья

X₁ Х₂ Х₄

Х₃

где: W_c(s) – передаточная функция исходной системы; W_к2(s) – передаточная функция корректирующего звена.

Местная обратная связь

Х₁ Х₂ Х₃

Х₄

где: W_c(s) – передаточная функция исходной системы; W_ос(s) – передаточная функция корректирующего звена.

Х₂ = Х₁ ± Х₄ Х₄ = W_ос(s) * Х₃

Х₃ = W_с(s) * Х₂ = W_с(s) [Х₁ ± W_ос(s)Х₃]

Отрицательная обратная связь: « + », положительная обратная связь: « - ». Обычно применяют отрицательную обратную связь.

Формулы перехода от корректирующего устройства одного типа к корректирующему устройству другого типа: