2. Типовые динамические звенья систем управления

Для исследования процессов в реальных системах пользуются идеализированными схемами, которые точно описываются математически и приближенно характеризуют реальные звенья систем в заданном диапазоне частот сигналов [1].

В общем случае передаточная функция системы может быть представлена в виде:

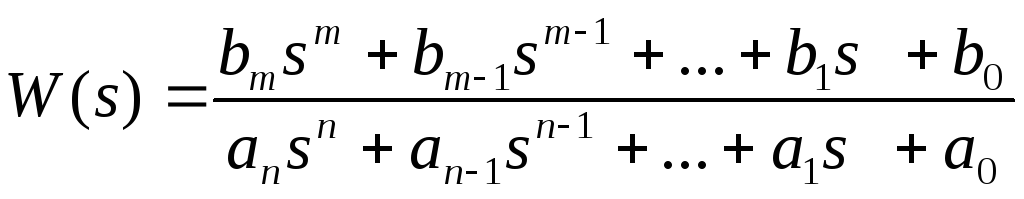
Звеном называют математическую модель элемента, соединения элементов или любой части системы.

Обычно система управления состоит из отдельных блоков, каждый из которых, чаще всего, описывается обыкновенными линейными дифференциальными уравнениями не выше второго порядка.

Рассматривая характеристики звеньев независимо от их назначения, физического принципа действия, мощности и скорости передаваемых сигналов, выделяют ряд типовых элементарных звеньев.

Усилительное (пропорциональное) звено

Уравнение звена:

где: x(t) - выход звена; u(t) - входное воздействие; K - коэффициент усиления (статический коэффициент передачи) звена.

С помощью усилительного звена передача сигнала от входа u(t) к выходу x(t)происходит мгновенно без какой-либо инерции. Поэтому усилительное звено называют еще пропорциональным, или безынерционным [1].

Передаточная функция усилительного звена:

Производя замену комплексной переменной s на jω, получим частотную характеристику усилительного звена:

Модуль выражения для W(jω) дает амплитудно-частотную характеристику (АЧХ) усилительного звена:

Поскольку мнимая часть в выражении для W(jω) равна нулю, то фазовая частотная характеристика (ФЧХ) будет равна нулю при всех частотах входного сигнала:

Логарифмическая амплитудно-частотная характеристика (ЛАЧХ) усилительного звена равна:

Интегрирующие звенья

Идеальное интегрирующее звено

Звено описывается дифференциальным уравнением первого порядка следующего вида:

где: k - коэффициент пропорциональности (усиления) звена.

Коэффициент k численно равен скорости изменения выходной величины при единичном значении входной величины.

Решая представленное выше дифференциальное уравнение получим:

Если начальные условия равны нулю, то, переходя к преобразованию Лапласа, получим передаточную функцию идеального интегрирующего звена:

Частотная характеристика интегрирующего звена равна:

АЧХ интегрирующего звена - это модуль частотной передаточной функции W(jω), т.е.:

ЛАЧХ интегрирующего звена:

При изменении частоты на одну декаду значение ЛАЧХ изменится на -20дБ. График ЛАЧХ представляет собой прямую линию с отрицательным наклоном.

ФЧХ интегрирующего звена равна:

Интегрирующее звено с замедлением

Звено описывается следующим дифференциальным уравнением [1]:

где: Т, k - постоянные параметры звена.

Передаточная функция звена равна:

Частотная характеристика звена равна:

АЧХ звена определяется выражением:

ЛАЧХ звена строится по выражению:

ФЧХ звена равна:

Изодромное звено

Дифференциальное уравнение изодромного звена имеет следующий вид [2]:

где: Т, k - постоянные параметры звена.

Передаточная функция звена равна:

Частотная характеристика звена равна:

АЧХ звена равна:

ЛАЧХ изодромного звена равна:

ФЧХ звена определяется как:

Дифференцирующие звенья

Идеальное дифференцирующее звено

Звено описывается следующим дифференциальным уравнением:

где: k - коэффициент пропорциональности (усиления) звена.

Выходная величина x(t) дифференцирующего звена пропорциональна скорости изменения входной величины u(t).

Передаточная функция идеального дифференцирующего звена:

Частотная характеристика звена равна:

Амплитудно-частотная характеристика звена:

ЛАЧХ дифференцирующего звена:

При изменении частоты на одну декаду значение ЛАЧХ изменится на +20дБ. График ЛАЧХ представляет собой прямую линию с положительным наклоном.

ФЧХ получается из условия, что действительная часть частотной передаточной функции равна нулю:

Идеальное дифференцирующее звено относится к физически нереализуемым звеньям. В технике не могут использоваться физически не реализуемые звенья, поэтому для дифференцирования сигналов (ускорения реакции системы) используется инерционно-дифференцирующее звено (дифференцирующее звено с замедлением).

Дифференцирующее звено с замедлением (инерционно-дифференцирующее звено)

Фактически это звено представляет последовательное соединение двух звеньев: идеально дифференцирующего и апериодического звена первого порядка.

Звено описывается дифференциальным уравнением вида:

где: Т, k - постоянные параметры звена.

Передаточная функция звена равна:

Частотная характеристика звена равна:

АЧХ звена равна:

ЛАЧХ определяется как:

ФЧХ звена определяется как:

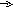Фазовые сдвиги, вносимые звеном, являются наибольшими при низких частотах. На высоких частотах фазовый сдвиг постепенно уменьшается, стремясь в пределе к нулю при ω ∞.

Апериодическое звено первого порядка

Звено описывается дифференциальным уравнением первого порядка с постоянными коэффициентами:

где: Т, k - постоянная времени и статический коэффициент передачи звена.

Постоянная времени звена характеризует его инерционные свойства, а статический коэффициент передачи (коэффициент усиления) представляет собой отношение выходного сигнала к входному в установившемся режиме (после завершения переходного процесса). Апериодическое звено первого порядка называют также инерционным звеном.

Передаточная функция звена равна:

Производя замену комплексной переменной s на jω, получим частотную характеристику инерционного звена:

АЧХ звена равна:

Из выражения для АЧХ следует, что чем меньше постоянная времени Т, тем меньше инерционность звена и более вытянута амплитудная характеристика вдоль оси частот, или, как считается, тем шире полоса пропускания частот у данного звена [1].

ЛАЧХ апериодического звена первого порядка:

ФЧХ звена определяется как:

Апериодическое звено второго порядка

Дифференциальное уравнение звена имеет следующий вид [1]:

где: Т₁ ≥ 2Т₂; Т₁, Т₂ - постоянные времени звена, k - коэффициент усиления звена.

Передаточная функция звена равна:

где

Производя замену комплексной переменной s на jω, получим частотную характеристику апериодического звена второго порядка:

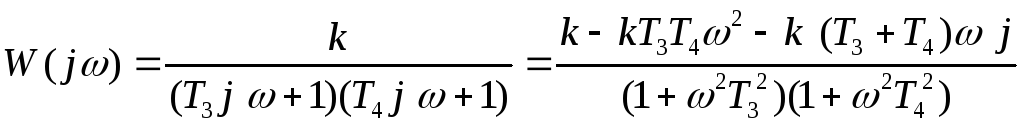
АЧХ звена равна:

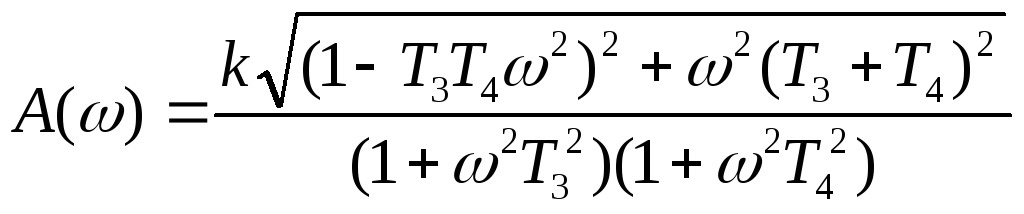
ЛАЧХ апериодического звена второго порядка:

ФЧХ звена определяется как:

Колебательное звено

Звено описывается дифференциальным уравнением второго порядка в двух формах:

где: Т₁ < 2Т₂, Т₁, Т₂ - постоянные времени звена, k - коэффициент усиления звена.

где: Т=Т₂ - постоянная времени колебательного звена,

0 < ξ < 1 - относительный коэффициент затухания (коэффициент демпфирования), ξ = Т₁ / 2Т₂.

Передаточная функция колебательного звена:

Производя замену комплексной переменной s на jω, получим частотную характеристику колебательного звена:

АЧХ звена равна:

ЛАЧХ колебательного звена:

Уравнение асимптотической ЛАЧХ имеет вид:

при ω < 1 / T

при ω ≥ 1 /T

Частота ω = 1 / Т называется сопрягающей.

Фазовую частотную характеристику колебательного звена представляют в следующем виде [4]:

при ω ≤ 1 / T

при ω > 1 /T

Консервативное звено

Консервативное звено является частным случаем колебательного звена при относительном коэффициенте затухания ξ=0. В консервативном звене не происходит рассеяния энергии.

Уравнение консервативного звена:

Передаточная функция консервативного звена:

Частотная характеристика звена равна:

АЧХ звена равна:

ЛАЧХ консервативного звена:

Фазовая частотная характеристика консервативного звена определяется:

при ω < 1 / T

при ω > 1 /T

Запаздывающее звено

Выходная величина в запаздывающем звене точно повторяет входную величину, но с некоторым запаздыванием по времени τ:

.

Найдем передаточную функцию запаздывающего звена, применив к приведенному уравнению прямое преобразование Лапласа, получим:

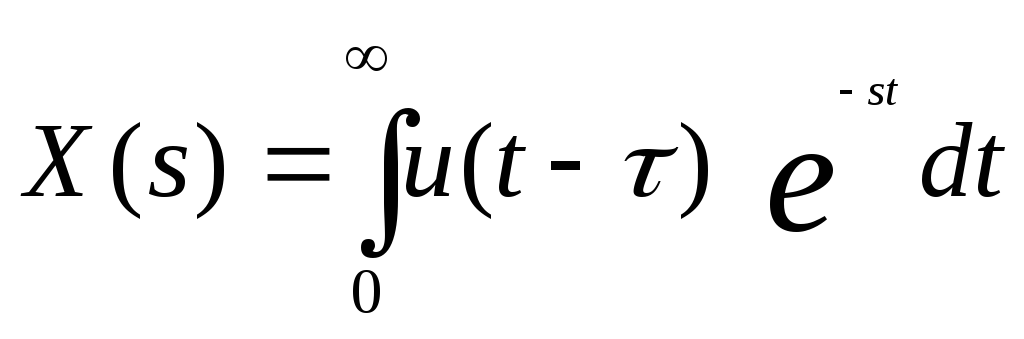
Введем новую переменную: z = t - τ:

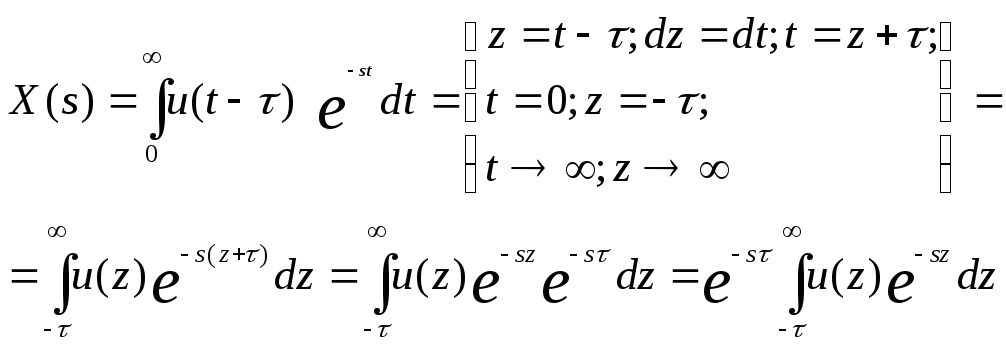
Поскольку преобразование Лапласа определяется в пределах от нуля до бесконечности, то полученное выражение следует интегрировать в пределах от нуля до бесконечности, т.е.:

В полученном выражении интеграл - это преобразование Лапласа от входной величины, поэтому:

Теперь найдем передаточную функцию, взяв отношение изображения по Лапласу выходной величины к изображению входной:

Частотная характеристика запаздывающего звена с учетом формулы Эйлера равна:

Амплитудно-частотная характеристика:

ЛАЧХ запаздывающего звена:

ФЧХ звена равна: