Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Московский педагогический государственный университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

23.12.2015 Шеина Г.В. Теория и практика решения задач по алгебре, часть 1

.pdf

Скачиваний:

126

Добавлен:

28.03.2016

Размер:

1.61 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 89 / 109 10 > Следующая >>>

ходного уравнения: y	u	p	, y	u	p	, y	u 2	p	.
ходного уравнения: y	u		, y	u	3u	, y	u 2	3u 2	.
4	1	3u	5	1	3u	6	1	3u 2
		1			1			1

Мы покажем, что вторая серия корней совпадает с первой серией, а именно имеют место равенства: y4 y1, y5 y3, y6 y2 .

Проверим первые два равенства. Действительно, по теореме Виета для приве-

денного квадратного уравнения произведение корней t1 t2

равно свободному

члену, то есть t t

, откуда после извлечения кубического корня из пра-

вой и левой части получим u u

. Значит, u

u y .

3u1

Кроме того,

. Но 3 1

2 и

. По-

этому y

u 2 y .

3u 2

Задача. Проверьте равенство y6 y2 .

В дальнейшем мы будем рассматривать только корни y1, y2 , y3 .

Общие формулы

Имеется уравнение y3 py q 0 . Находим корни последующим формулам,

приведенным ниже в рамке. Для первого корня имеем



u 3	q	q2		p3	, v	p	, y u v	.
u 3					, v		, y u v	.
2		4	27			3u	1
2		4	27			3u

			p 2													2
	p		p 2					p	1			3				2		1			3
Поскольку															i							i v , то для второго
Поскольку															i							i v , то для второго
	3u		3u			3		u	2			2						2		2
							v
									1		3		3		i
															i
									4		4	2

					p					1				3					1			3		1	3
корня имеем: y 2		u				u											i v						i u			i v
корня имеем: y 2		u		3u		u				2		2					i v		2		2		i u	2	2	i v
				3u						2		2							2		2			2	2

или, в другой форме,


				y					1		(u v) i						3			(u v)				.
				y	2				2		(u v) i					2				(u v)				.
					2

Для третьего корня имеем:								p						p	v . Поэтому
Для третьего корня имеем:							3u 2							3u	v . Поэтому
							3u 2							3u

	p							1				3						1				3
y3 u 2			u 2 v										i	u									i v			или, в другой форме,
y3 u 2	3u	2	u 2 v					2				2	i	u				2				2	i v			или, в другой форме,
	3u							2				2						2				2


					y					1		(u v) i							3		(u v)				.
					y	3						(u v) i									(u v)				.
						3			2									2
									2									2

Частный случай. Кратные корни

Напомним, что если p 0 или q 0, то уравнение y3 py q 0 можно решить без применения рассматриваемых нами формул. Поэтому будем считать, что

p 0, q 0 . Обозначим выражение									q2				p3		символом . Рассмотрим случай
p 0, q 0 . Обозначим выражение															символом . Рассмотрим случай
									4			27
0 . Имеем:		0		q2		p3		0			q2				p3	.
0 . Имеем:		0						0								.
			4		27				4					27
		4 p3
Поэтому q	2	4 p3	и u		3		q	q 3	1				q 3					1		3q
																					.
		27					2			2q2							2		4 p3	2 p	.

																		27
																		27

Ясно, что u													3q			0 . Покажем, что v u . Действительно, v																																							p	и равенство
Ясно, что u												2 p				0 . Покажем, что v u . Действительно, v																																							3u	и равенство
												2 p																																											3u
v u равносильно равенствам:
														p																							3q 2														9q2
																u 3u2 p																3									p 3													p
														3u		u 3u2 p																3									p 3										4 p		2	p
														3u																						2 p															4 p
																					27q2				p3									q2									p3			0 0 .
																									p3																					0 0 .
																					4														4					27
Значит, y u v 2u																						3q		,
Значит, y u v 2u																								,
									1													p
																						p

y					1			(u v) i									3	(u v) u, y																					1	(u v) i									3	(u v) u .
y	2							(u v) i										(u v) u, y											3											(u v) i										(u v) u .
	2			2												2													3						2													2
				2												2																			2													2

Окончательно получаем																							0 y													3q				, y					y						y1		.
																															1													2

																																						p									3				2
																																						p													2

Пример. Решим уравнение y3																											4	y							16					0 .
Пример. Решим уравнение y3																												y												0 .
																									3										27
Имеем неполное уравнение, для которого
p				4			, q						16			. Поэтому										q2							p3								162							43				0
p				3			, q					27				. Поэтому																									4 272							27 33				0
				3								27													4								27								4 272							27 33
						3q					3 16								4											4												2
и		y				3q								27					4	,		y		y						4												2		.
и		y	1									4								,		y	2	y																				.
			1				p												3				2		3					2 3										3
							p												3											2 3										3
												3
									4	,		2			,		2
Ответ:																			.
Ответ:																			.
									3			3					3

Сведение полного уравнения к трехчленному уравнению

Рассмотрим общее уравнение третьей степени над полем комплексных чисел:

Ax3 Bx2 Cx D 0 , где A, B,C, D .

Будем считать, что старший коэффициент не равен нулю (иначе это будет квад-

ратное или даже линейное уравнение, а такие уравнения мы решать умеем). То-

гда можно разделить на старший коэффициент обе части уравнения и получить следующее приведенное уравнение: x3 bx2 cx d 0. Сделаем замену x y

и преобразуем получившееся уравнение:

y 3 b y 2 c y d 0 ,

y3 3 b y2 3 2 2b c y 3 b 2 c d 0.

Ясно, что коэффициент при степени y2 можно обратить в нуль, для чего доста-

точно положить b3 . Таким образом, осуществив замену x y b3 , получим

неполное (или трехчленное) уравнение y3 py q 0 .

x3 bx2 cx d 0 если x y b3 , то y3 py q 0

Кубические уравнения с действительными коэффициентами

Будем считать теперь, что коэффициенты p и q в уравнении y3 py q 0 –

действительные числа.

Случай 1. Кратные корни

Этот случай рассмотрен ранее. Формулы для случая действительных коэффи-

циентов остаются прежними, то есть

0 y1	3q	, y		y3	y1	.
0 y1	p	, y	2	y3	2	.
	p				2

				Случай 2. Три различных действительных корня
Пусть		q2			p3	0. Ранее мы рассмотрели квадратное уравнение

			4	27
t2 qt	p3		0 , где t z3 . Теперь это уравнение имеет действительные коэффи-

27

циенты. Дискриминант данного квадратного уравнения равен q2 p3 . Он

4 27

отрицателен, поэтому корни t1 u3 , t2 v3 этого квадратного уравнения ком-

плексны (и не являются действительными) и комплексно сопряжены, то есть

Imu 0 и v3 u3 u 3 . Поэтому имеет место один из трех случаев v u , или

v u , или v u 2 , где – корень кубический из единицы. Поскольку по тео-

реме Виета для квадратного уравнения произведение корней равно свободному

члену уравнения, то есть t t															u3 v3					p3		, и из равенства u3									v3		p3
члену уравнения, то есть t t														2	u3 v3							, и из равенства u3									v3
										1				2					27													27
																			27													27
можно извлечь действительный кубический корень. Тогда uv																														p		. Если
можно извлечь действительный кубический корень. Тогда uv																																. Если
																												3
v u , то uv uu											u	2			. Условие v										2 также приводит к случаю
v u , то uv uu											u	2			. Условие v								u		2 также приводит к случаю
uv uu 2			u		2 2						. Поэтому остается случай v																.

																										u
Поскольку u u 2Reu и u u 2Imu , получаем, что формулы

																						1						3
y u v, y								1	(u v) i				3		(u v) , y							1		(u v) i				3	(u v) примут теперь
y u v, y		2							(u v) i						(u v) , y			3						(u v) i					(u v) примут теперь
1		2		2									2					3			2							2
				2									2								2							2
следующий вид:

																q
	y u						, 2Reu 2Re 3										;
						u
						u
	1														2
															2


					1								3					1							3
	y						(u v) i							(u v)						(u				) i		(u				) Reu 3 Imu ,
		2																					u					u
																							u					u
			2								2				2										2
			2								2				2										2

				1								3				1									3
	y					(u v) i								(u v)					(u					) i		(u			) Reu 3 Imu .
		3																				u					u
																						u					u
			2								2				2										2
			2								2				2										2
	Окончательно имеем

								q2		p3							q
p, q			, =					q2		p3	0 u 3						q				, y 2Reu, y										2, 3	Reu 3 Imu	.
p, q			, =								0 u 3										, y 2Reu, y											Reu 3 Imu	.
			4						27						2						1
			4						27						2

Заметим, что выписанные корни действительны и различны, поскольку

Imu 0.

Пример 1. ( 0 . Три различных действительных корня).

Решим уравнение y3 6 y 4 0.																Имеем p 6, q 4 . Вычислим :
	q2			p3			42	63			4 8 4					. Следовательно, 0 , то есть уравнение
								63			4 8 4					. Следовательно, 0 , то есть уравнение
4				27		4			27
имеет три различных действительных корня. Для нашего примера

																	3		3
			q					3
			q					3
u 3										2	2i 3			2 2 cos				isin
u 3			2							2	2i 3			2 2 cos			4	isin
			2														4		4
													1			1
													1			1
2		cos				i sin						2			i		1 i , то есть u 1 i . Но тогда
2		cos				i sin						2			i		1 i , то есть u 1 i . Но тогда
					4				4				2			2

y1 2Reu 2, y2 Reu 3 Imu 1 3, y3 Reu 3 Imu 1 3 .

Ответ: 2; 1 3 .

Замечание. Вычисление кубического корня 3 q2 не всегда является про-

стым делом. Однако если этот корень можно представить в виде a bi , где a,b , то вычисление значительно упрощается.

Пример 2. ( 0 . Три различных действительных корня).

Решим неполное уравнение y3 39 y 18 0, p 39, q 18 . Вычислим дис-

криминант :	q2		p3	182	393	81 133 81 2197 2116 и

4		27		4	27

2116 46i . Найдем кубический корень u 3 q2 39 46i в алгебра-

ической форме. Для этого представим его в виде u a bi . Тогда

(a bi)3 9 46i . Вычислим модуль левой и правой части.

(a bi)	3	a bi	3	a	2

b	2	3
b			;

9 46i 92 462 81 2116 2197 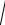133 13 3 .

Значит, a2 b2 13.

Будем искать целые значения для коэффициентов a и b . Для этого предста-

вим 13 в виде суммы квадратов целых чисел: a2 b2 13 9 4 4 9. Значит,

a 2,b 3a 3,b 2 .

Но (a bi)3 a3 3ab2 i( b3 3a2b) 9 46i .

Поэтому для случая a 2,b 3 имеем

(a bi)3 a (a2 3b2 ) i b (3a2 b2 ) 9 46i .

2 4 27 23 3 12 9 3

Во втором случае a (a2 3b2 ) i			b	(3a2 b2 ) 9 46i , если a 3,b 2 .
3 9 12 3			2	27 4 23
Имеем равенство 9 46i (3 2i)3 . Поэтому u 3 2i . Тогда

y1 2Reu, y 2 Reu		3 Imu, y3	Reu 3 Imu , то есть

y1 2 3 6, y 2, 3 3	3 2 .

Ответ: 6; 3 23 .

Случай 3. Один действительный и два

сопряженных комплексных корня

Рассмотрим оставшийся случай: q2 p3 0 . Покажем, что тогда имеется

4 27

один действительный корень и два комплексно сопряженных корня. Корни

квадратного уравнения t2 qt

p3 0 , где t z3 , дискриминантом которого

является , есть различные действительные числа, то есть t1, t2

, t1 t2 и

p 3

t1 t2

. Поскольку

— действительное число, в качестве

u и выбираем действительное значение кубического корня, то есть

u 3

– действительное число. Но uv

, поэтому v также

есть действительное число, то есть v

. Поскольку t

v3 , то u v .

Итак, u, v

и u v

, u v

. Формулы для нахождения корней остаются

такими же, как и в общем случае

u 3

, v

, y1 u v, y 2

u v i

u v

Условие u v,

u v

означает, что корень y1 — действительное число. Кор-

ни y2 и y3 не являются действительными и комплексно сопряжены, поскольку u v и u v .

Пример. Решим уравнение y3 6 y 9 0 . Имеем																										p 6, q 9 и
	p3					q2		63				92		8		81				81 32		49			7	2
																										. Тогда
																										. Тогда
	27				4			27				4				4				4			4		2
																			6
u 3		9				7	3			2, v					p						1 и y			u v 2 1 3,
		9				7			8						p								1
									8
	2				2										3u			3 2
	2				2										3u			3 2

y 2			1	u v i								3	u v				1		2 1 i				3	2 1			3	1
			1									3					1						3				3	1	i 3	,
			2								2											2						2	i 3	,
			2								2					2						2				2		2

y3 y2 32 12 i 3 .

	3	1		3	1
	3	1		3	1
Ответ: 3,			i 3,			i 3	.
Ответ: 3,			i 3,			i 3	.
	2	2		2	2

Уравнения четвертой степени. Метод Феррари

Рассмотрим уравнение x4 ax3 bx2

cx d 0 , где a, b,

c, d .

Феррари предложил представить многочлен x4 ax3

bx2

cx d разности

квадратов следующим образом:

cx d x

, где , , .

Учтем, что

						2 2									2 2					2 2 2 .
Раскрыв скобки в равенстве															и приведя подобные, получим
	2				a	2 x 2				2		ax					2	x				2
bx		cx d						2 x															или
bx		cx d						2 x															или
						4						2
x			2	a 2 x 2					2		ax					2			2
							2	x									bx			cx d . Преобразовав правую часть
							2	x									bx			cx d . Преобразовав правую часть
					4						2
равенства, получим: x													2	x2			b 2				a 2		x c a	d 2 .

																					4
																					4

Выражение справа должно быть полным квадратом. Это будет так, если дис-

криминант квадратного трехчлена, стоящего слева, обратится в 0. Вычислим этот дискриминант и приравняем его к нулю:

D c a				2	4	b 2	a 2		d 2 0 . Тогда

							4

		2
	c a		4		b 2 1 / 4a2			d 2		0

c2 2ca 4bd 4b 2 8 d 8 3 a2d 08 3 4b 2 2ca 8d c2 4bd a2d 0.

Последнее уравнение является кубическим относительно и всегда имеет ко-

рень в поле . Поэтому число может быть найдено, а значит, будут опреде-

лены и числа , и тем самым левая часть уравнения x4 ax3 bx2 cx d 0

будет представлена в виде разности квадратов. Разлагая ее в произведение и приравнивая каждый сомножитель к нулю, получим два квадратных уравнения,

из которых и найдем 4 корня исходного уравнения.

Замечание.

В случае действительных коэффициентов a,b,c, d и действительного числа

получаем квадратный трехчлен	x2	b 2	a 2	x c a d 2

			4

с действительными коэффициентами, который можно записать в виде

Ax 2 Bx C , где A b 2 a2 , B c a , C 2 d . В случае, когда
	4
B2 4AC 0, получаем B2 4AC , то есть AC 0 . При условии, что
A 0,C 0 , имеем B signB 2	AC и
Ax 2 Bx C Ax 2 2sign(B)	AC x C Ax sign(B) C 2 .

В этом случае для полного квадрата

<<< < Предыдущая 1 2 3 4 5 6 7 89 / 109 10 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
19.09.20192.95 Mб26209371_7777D_yasyukova_lyudmila_apollonovna_psi...doc
#
17.11.2019441.34 Кб20209_-_208_208_188_209_-_208_208.doc
#
24.04.201966.05 Кб421 - 25.doc
#
23.09.201940.55 Кб1323 билет (4).docx
#
06.06.2015218.62 Кб1423-24.doc
#
28.03.20161.61 Mб12623.12.2015 Шеина Г.В. Теория и практика решения задач по алгебре, часть 1.pdf
#
06.06.201559.9 Кб2424.01.doc
#
06.06.201586.53 Кб525 билетов.doc
#
23.09.201923.82 Кб825-28.docx
#
27.08.2019181.76 Кб5258540_ED361_samohina_t_s_dianova_e_m_upgrade_y...doc
#
04.08.201949.36 Кб1326-29.docx