
- •1.5. Содержание заданий срс модуля 1
- •Типовое задание ргр № 1. Анализ внутренних силовых факторов
- •1.1. Анализ распределения нормальных сил
- •1.2. Анализ распределения крутящих моментов
- •1.3. Анализ внутренних силовых факторов при изгибе
- •1.4. Дифференциальные зависимости между изгибающим моментом, поперечной силой и интенсивностью поперечной распределенной нагрузки
1.5. Содержание заданий срс модуля 1
по курсу «Механика радиотехнических систем
(Прикладная механика)»
Модуль 1
ПРИМЕРЫ РЕШЕНИЯ ТИПОВЫХ ЗАДАЧ
Тема 1. Статика. Законы равновесия механических систем
Пример 1.Определить равнодействующую
двух силP1 = 10HиP2
= 25H, приложенных в
одной точке под углом друг к другуα
= 60˚.Найти также углы![]() и
и![]() ,
образуемые равнодействующей с
соответствующими силами (рис.1).
,
образуемые равнодействующей с
соответствующими силами (рис.1).
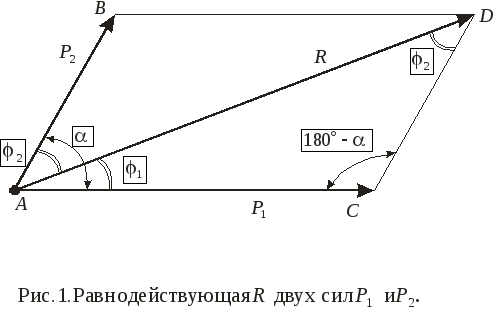
Решение. По теореме косинусов находим равнодействующую силу:
R2
= P![]() + P
+ P![]() – 2P1P2cos(180˚ –α);
– 2P1P2cos(180˚ –α);
R=
![]() Н.
Н.
По теореме синусов запишем
![]() .
.
Отсюда
sin![]() =
=
![]() sin
α =
sin
α =
![]() = 0,694;
= 0,694;
sin![]() =
=
![]() sin
α =
sin
α =
![]() = 0,277;
= 0,277;
![]()
![]() 44˚;
44˚; ![]()
![]() 16˚.
16˚.
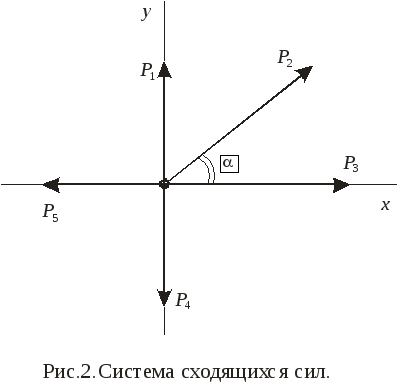
Пример 2.Найти величину равнодействующей системы пяти сходящихся сил:P1 = 3H,P2 = 5H,P3 = 6H,P4 = 7H,P5 = 2H(рис. 2), еслиα = 45˚.
Решение. Определяем проекцию равнодействующей на осиxиy:
Px =
–P5
+ P2cos
α +
P3
= –2 +![]() + 6 = 7,54 Н;
+ 6 = 7,54 Н;
Py = P1 – P4 + P2sin α = 3 – 7 + 3,54 = –0,46 Н.
Затем находим величину равнодействующей силы:
R=![]()
![]() 7,54
Н.
7,54
Н.
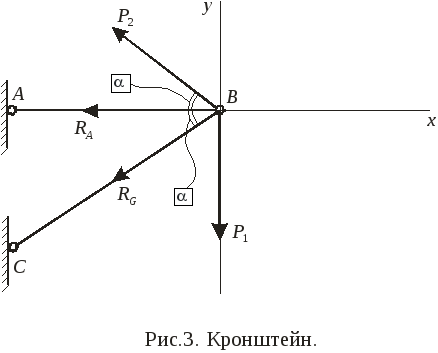
Пример 3.К шарнируBкронштейнаABC (рис. 3) приложены силыP1 = 20HиP2 = 15H.Определить усилия в стержняхABиBC, пренебрегая весом стержней, еслиα = 30˚.
Решение. Рассмотрим равновесие шарнираВ. Действие связей-стержней на шарнирВзаменяем реактивными силамиRAиRC.
Составляем уравнения равновесия в системе координат xBy:
![]() ;
– RA
–
P2cos
α –
RC cos
α = 0;
;
– RA
–
P2cos
α –
RC cos
α = 0;
![]() ;
P2sin
α –
RC sin
α
– P1
= 0.
;
P2sin
α –
RC sin
α
– P1
= 0.
Из второго уравнения находим RC= –25 Н, из первого уравненияRA= 8,7 Н. Таким образом, стерженьАВсжат, стержень ВСрастянут.
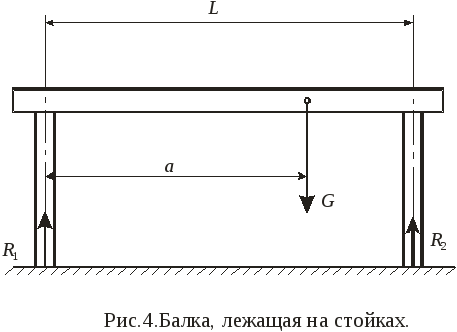
Пример 4.К балке, лежащей на стойках 1 и 2 (рис.4), подвешен грузG=100H. Расстояние между стойкамиl = 1 м. На каком расстоянииaот стойки 1 нужно подвесить груз, чтобы нагрузка на нее не превышала 20 Н?
Решение. Силы давления на стойки 1 и 2 обозначимR1иR2соответственно. Сила давленияR1 по условию равна 20 Н. РавнодействующаяGраскладывается на две параллельные составляющие:G=R1+R2.
Откуда R2=G–R1= 80 Н.
Составляем пропорцию
![]() ,
,
откуда находим
a =![]() =
=
![]() = 0,8 м.
= 0,8 м.
Пример 5.Балка шарнирно закреплена в опореАи положена на катокВ(рис. 5). Определить реакции в опорах, еслиР= 2 Н.
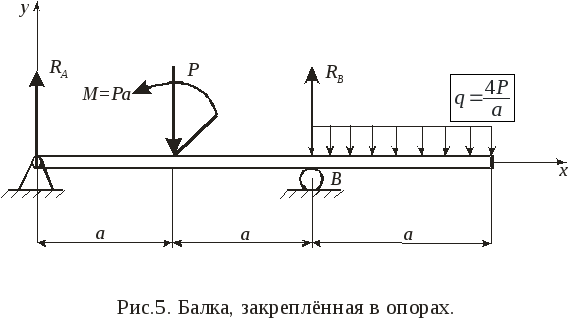
Решение. Выбираем систему координатxAy. Освобождаем балку от связей. Реакция неподвижного шарнираА будет направлено по осиу, поскольку в горизонтальном направлении по осихактивные силы не действуют. Реакция подвижной опоры (катка)RBперпендикулярна к опорной поверхности катка.
Сила Рявляется сосредоточенной,
а нагрузка интенсивностиqраспределена равномерно на участке
балки длиннойа. Интенсивность
нагрузки имеет размерность силы,
деленной на длину, например Н/м.
Интенсивность находят из соотношенияq = dQ/dx.
Равнодействующую нагрузки получаем
интегрированием этого выражения по
длине участка:Q =
![]()
Точка приложения равнодействующей равномерно распределенной нагрузки находится в середине участка, на котором она действует. Графически распределенную нагрузку изображают над или под брусом (рис. 5).
Составим уравнение равновесия балки:
![]() ,
M –
Pa
+
RB 2a
– (qa)
2,5a = 0,
,
M –
Pa
+
RB 2a
– (qa)
2,5a = 0,
откуда
PA
– PA
+
RB 2a
–
![]() a
a
![]() a
= 0, RB
=5Р
= 10 Н.
a
= 0, RB
=5Р
= 10 Н.
Из уравнения равновесия
![]() ;
;
получим
RA + RB –Р –qa = 0;
RA + 5Р –Р –4Р = 0;
RA = 0.
Пример 6. К вертикальному брусу, заделанному нижним концом в основание, приложены силыР1,Р2;Р3– вес бруса (рис. 6). Определить реакции в заделке, еслиР1= 2 кН,Р2= 2 кН,Р3= 4 кН,α = 45˚.
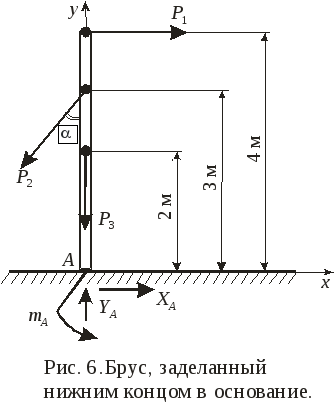
Решение. Выбираем систему координатxAy. Освобождаем брус от связи – жесткой заделки, заменяя ее неизвестной реактивной силойRAс составляющими по координатным осямХА, YАи парой с неизвестным моментомmА. Составляем уравнение равновесия бруса в виде
![]() ;ХА + P1
– Р2sinα= 0;ХА
;ХА + P1
– Р2sinα= 0;ХА ![]() 0,41 кН;
0,41 кН;
![]() ;YА – P3 – Р2cosα= 0;YА
;YА – P3 – Р2cosα= 0;YА ![]() 5,41 кН;
5,41 кН;
![]() ;
– P14
+ Р2sin
α3 + mA
= 0; mA
= –3,76 кН.
;
– P14
+ Р2sin
α3 + mA
= 0; mA
= –3,76 кН.
Знак «минус» в решении третьего уравнения показывает, что истинное направление реактивного момента mAбудет противоположно показанному на рис. 6.
Пример 7.Квадратная прямоугольная
плита размер l= 4 м (![]() = 45˚), весомР= 20 кН удерживается в
горизонтальном положении тросомКС,
цилиндрическим подпятником Ви
шарниромА(рис. 7). Определить реакции
связей, если угол между тросом и плоскостью
плитыα = 45˚.
= 45˚), весомР= 20 кН удерживается в
горизонтальном положении тросомКС,
цилиндрическим подпятником Ви
шарниромА(рис. 7). Определить реакции
связей, если угол между тросом и плоскостью
плитыα = 45˚.
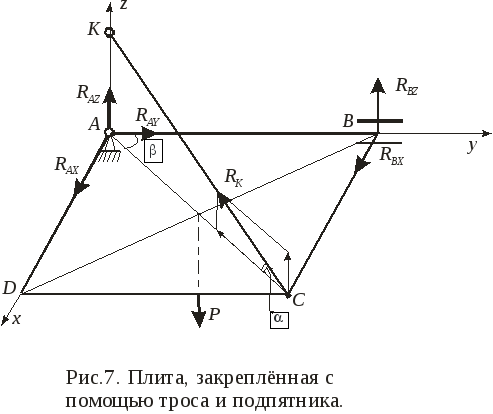
Решение.Освободим плиту от связей. Реактивную силу в шарниреАзаменим тремя составляющимиRAX,RAY,RAZ реакцию подшипникаRBзаменим двумя составляющимиRBX,RBZ. Реакция тросаRKнаправлена по тросу, ее проекция на осьz
RКZ
= RK
sin α
= RK
![]() ,
,
а проекции на оси x, yравны:
RКX
= RКY
= RK
sin α
cos![]() = RK
/2.
= RK
/2.
Составляем уравнение равновесия плиты:
![]() ;
RAХ
+
RBХ
– RКX
= 0;
;
RAХ
+
RBХ
– RКX
= 0;
![]() ;
RA
Y
– RКY
= 0;
;
RA
Y
– RКY
= 0;
![]() ;
RAZ
– P
+ RKZ
+ RBZ
= 0;
;
RAZ
– P
+ RKZ
+ RBZ
= 0;
![]() ;
–
;
–![]() + RBZ
+ RBZ
![]() +
RKZ
+
RKZ
![]() =
0;
=
0;
![]() ;
;![]() –RKZ
–RKZ![]() =
0;
=
0;
![]() ;RBX
;RBX![]() =
0.
=
0.
Из уравнений находим
RAХ
= RAY
= P
![]() ;
RAZ
=
;
RAZ
= ![]() ;
;
RBХ = RBZ = 0;
RKХ
= RKY
= P
![]() ;
RKZ
=
;
RKZ
= ![]() .
.
Пример 8. Горизонтальный вал (рис. 8) длинной 2l= 100 мм установлен в подшипникеАи подпятникеВ. На валу закреплено колесо, на которое действуют силы: окружнаяFt= 100 Н, радиальнаяFR= 37 Н, осеваяFa= 18 Н. Диаметр колесаd= 200 мм. Определить в положении равновесия моментmи реакции опорАиВ.
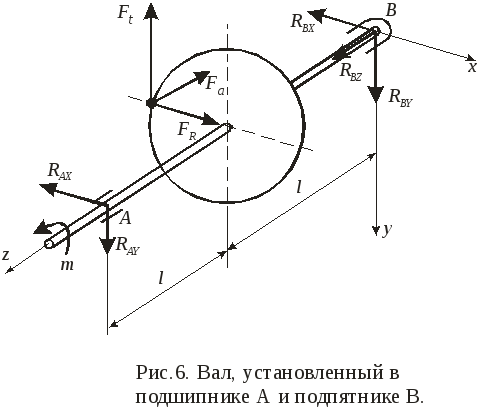
Решение.Освободим вал от связей. ПодшипникАвоспринимает только радиальную силу, которую представим двумя составляющимиRAХ , RAY . ПодпятникВ воспринимает радиальную и осевую силы:RBХ , RBY , RBZ.
Составляем уравнение равновесия вала:
![]() ;
FR –
RАX
– RВX
= 0;
;
FR –
RАX
– RВX
= 0;
![]() ;
RA
Y
+ RBY–
Ft
=
0;
;
RA
Y
+ RBY–
Ft
=
0;
![]() ;
RBZ
– Fa
= 0;
;
RBZ
– Fa
= 0;
![]() ;
RAY
2
;
RAY
2 ![]() –
Ft
–
Ft
![]() =
0;
=
0;
![]() ;
RAX
2
;
RAX
2 ![]() –
Fa
–
Fa
![]() – FR
– FR
![]() =
0;
=
0;
![]() ;m –Ft
;m –Ft
![]() =
0.
=
0.
Из уравнений находим
m= 10 Нм; RAХ = 0,5H; RAY = 50H;
RBХ = 36,5 H; RBY = 50 H; RBZ = 18 H.
Пример 9.Определить координаты центра тяжести пластины, показанной на (рис. 9).
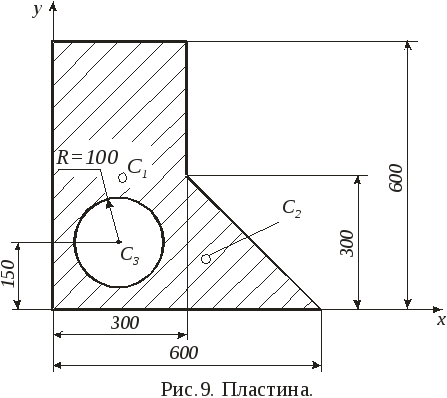
Решение.Разбиваем пластину на три фигуры: прямоугольник один без учета отверстия, треугольник 2 и круг 3, площадь которого как отверстия считаем отрицательной. Вычисляем площади фигур:
F1= 300![]() 600
= 18
600
= 18![]() 104мм2 ;
104мм2 ;
F2=
![]() = 4,5
= 4,5![]() 104мм2 ;
104мм2 ;
F3=
![]() = 3,14
= 3,14![]() 104мм2 .
104мм2 .
Определяем координаты центров тяжести фигур в выбранной системе координат. Центр тяжести треугольника находится в точке пересечения его медиан на расстоянии одной трети длины каждой медианы от соответствующей стороны треугольника: у1= 300 мм,х1= 150 мм,у2= 100 мм,х2= 400мм,у3= 150 мм,х3 = 150 мм.
Определяем координаты центра тяжести пластины:
yc
=
![]() мм;
мм;
хc =
![]() мм.
мм.
