- •Глава 5
- •5.5.1. Последовательный колебательный контур
- •Резонансная характеристика последовательного колебательного контура
- •Резонанс в связанных колебательных контурах
- •5.6. Операторные функции цепи
- •Глава 6
- •6.4.2. Передача импульсных сигналов через интегрирующую цепь
- •4) Найдем показатели экспоненты р1 и p2.
- •6.6. Расчет переходных характеристик последовательного колебательного контура
4) Найдем показатели экспоненты р1 и p2.
Коэффициенты р1, p2 находят, как корни характеристического уравнения:
![]()
отсюда
![]() .
.
Найдем постоянные интегрирования А1, А2.
Их находят из начальных условий, т.е. при t = +0, для искомой функции и ее производных. Значения токов и напряжений в начальный момент времени после коммутации (при t = +0) определяют из схемы замещения исходной цепи (рис. 6.24, б), образованной после коммутации (с учетом законов коммутации), по законам Кирхгофа. При нулевых начальных условиях наличие индуктивности равносильно разрыву цепи (iL(–0) = iL(+0)), а емкости – короткому замыканию (uC(–0) = uC(+0)).
Аналогичную схему замещения можно получить, если считать, что ступенчатому сигналу в начальный момент времени (t = +0) соответствует гармонический с бесконечно большой частотой (ω ∞).
Схема после коммутации (при t = +0, ω ∞) приведена на рис. 6.25, б, а произвольные постоянные A1 и А2 находят из уравнений:
![]() ;
;
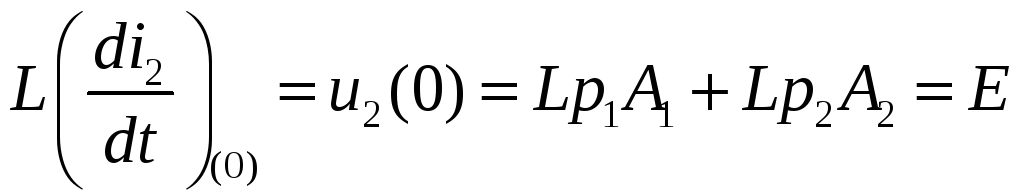 .
.
Из этой системы
находим
![]() .
.
Запишем общее решение относительно u2(t):
![]() .
.
Окончательное решение зависит от характера корней характеристического уравнения:
а)
если
![]() ,
то решение равно сумме экспонент (рис.
6.25, а),
оно не периодическое и его (режим
переходного процесса) называют
апериодическим;
,
то решение равно сумме экспонент (рис.
6.25, а),
оно не периодическое и его (режим
переходного процесса) называют
апериодическим;
б) если
![]() ,
то корни будут комплексными
,
то корни будут комплексными
![]() .
В этом случае решение представляет
собой гармоническую функцию времени,
убывающую по экспоненте (рис. 6.25, б).
Такое решение (режим переходного
процесса) называют колебательным;
.
В этом случае решение представляет
собой гармоническую функцию времени,
убывающую по экспоненте (рис. 6.25, б).
Такое решение (режим переходного
процесса) называют колебательным;
|
exp1 exp1+exp2 exp2 e–t а б |
|
Рис. 6.25 |
Отсюда условием критического режима
![]() ;
;
![]()
является соотношение Q = 2.
6.6. Расчет переходных характеристик последовательного колебательного контура
Схема последовательного колебательного контура приведена на рис. 6.26, а.
Для расчета переходной
характеристики установим связь между
выходным u2 и
входным u1 напряжениями.
Входной сигнал имеет вид ступенчатого
напряжения
![]() ,
тогда переходная характеристика h(t)
находится из выражения h(t)
= u2(t)/E,
где u2(t) – выходное
напряжение.
,
тогда переходная характеристика h(t)
находится из выражения h(t)
= u2(t)/E,
где u2(t) – выходное
напряжение.
|
C C R R а б u2()
= E u2(0)
= 0 u2(t) E u1(t) L C R L E L i(0)
= 0 в |
|
Рис. 6.26 |
Задачу будем решать классическим способом. За переменную в составляемом уравнении выбираем переменную, характеризующую энергетическое состояние цепи и наиболее просто связанную с выходным сигналом. Такой переменной является напряжение на конденсаторе uС(t) = u2(t).
1) Составим дифференцирующее уравнение относительно переменной состояния цепи и приведем его к стандартному виду.
Данная цепь представляет контур, а потому, используя второй закон Кирхгофа и соотношения между напряжениям и токами на элементах схемы, запишем:
![]() ;
;
![]() ,
,
![]() .
.
Отсюда
![]() ;
;
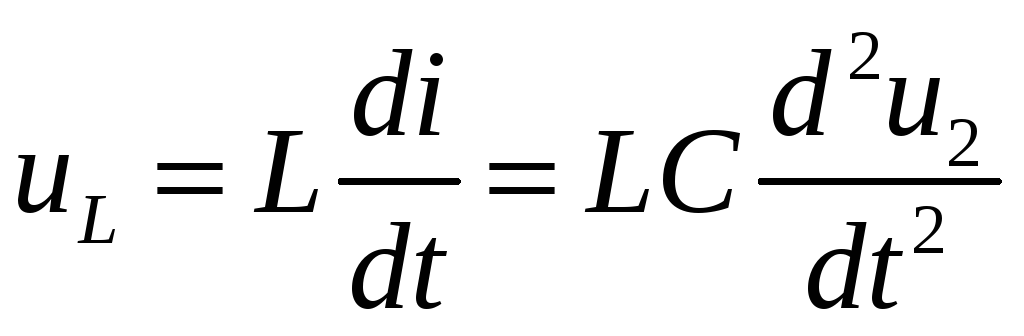 .
.
Подставим полученные напряжения в первое выражение:
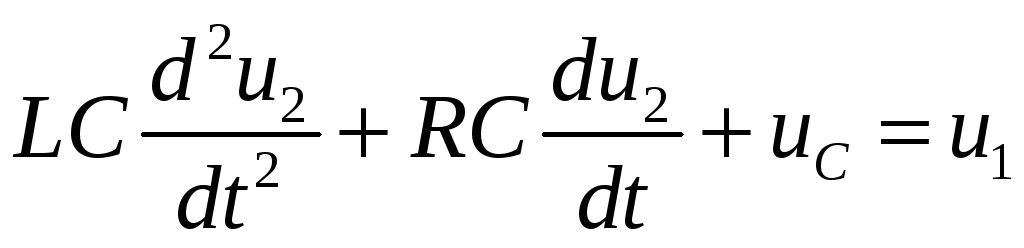 .
.
Поделим на LC
и введем обозначения
![]() .
.
Получим
![]()
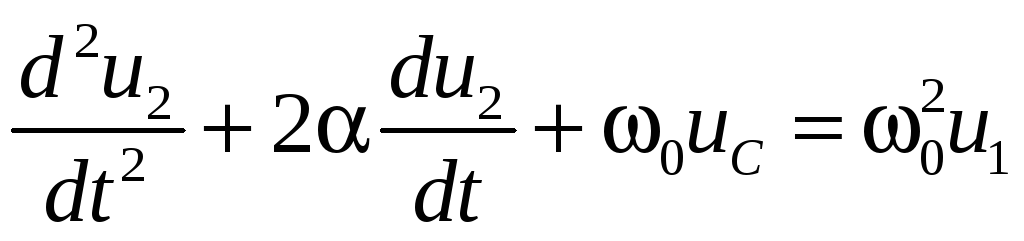 .
.
2) Запишем общее решение.
Оно зависит от выходного сигнала. Если выходной сигнал ступенчатый, то отклик записывается так:
![]() .
.
3) Найдем вынужденную
составляющую общего решения
![]() .
.
Для этого составим
схему замещения исходной цепи при t
∞,
![]() (рис. 6.26, б), из которой и получим,
что u2(=0)= E.
(рис. 6.26, б), из которой и получим,
что u2(=0)= E.
4) Найдем показатели экспоненты р1 и p2.
Коэффициенты
![]() находят, как корни характеристического
уравнения:
находят, как корни характеристического
уравнения:
![]() .
.
Отсюда
![]() .
.
5) Найдем постоянные интегрирования А1, А2.
Их находят из начальных условий, т.е. при t = +0 для искомой функции, ее производных и послекоммутационной схемы (при t = +0, ω ∞), которая приведена на рис. 6.26, в. Составим систему
![]() ;
;
 ,
,
из решения которой и находим А1 и А2
![]() .
.
6) Анализ корней и запись окончательного решения:
а) если
![]() ,
то корни
,
то корни
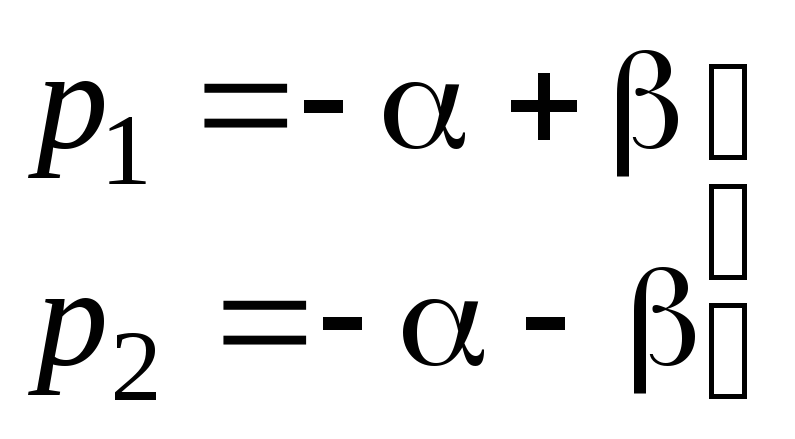 –
отрицательные действительные числа. И
окончательное решение записывается
так:
–
отрицательные действительные числа. И
окончательное решение записывается
так:

Учитывая, что
![]() ;
;
![]() ,
а также, что при βt
0,
,
а также, что при βt
0,
![]() ,
окончательно получим:
,
окончательно получим:
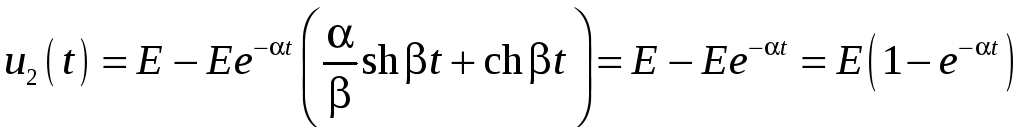 .
.
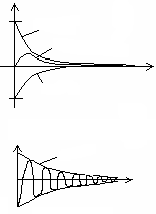
Такое решение называется апериодическим (рис. 6.27).
|
E u2 >
0 t |
|
Рис. 6.27 |
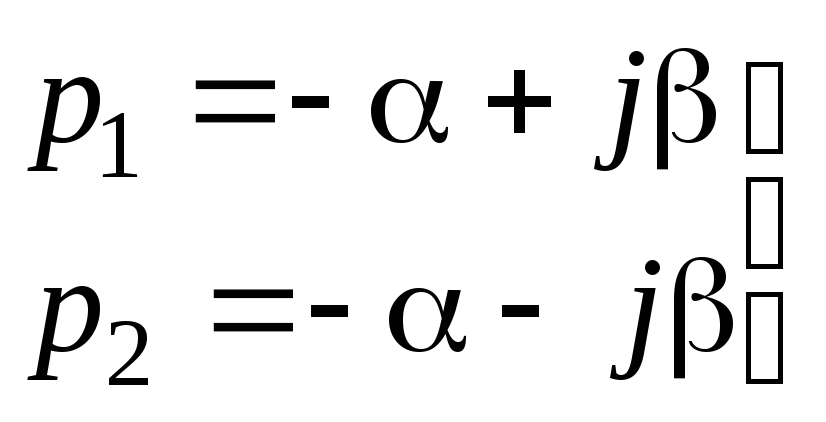 комплексно сопряженные числа. Если
проделать то же самое и учесть, что
комплексно сопряженные числа. Если
проделать то же самое и учесть, что
![]() ;
;
![]() ,
,
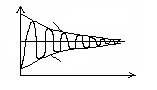
то при α << β, получим следующее (рис. 6.28):
|
E t =
0– e–t |
|
Рис. 6.28 |
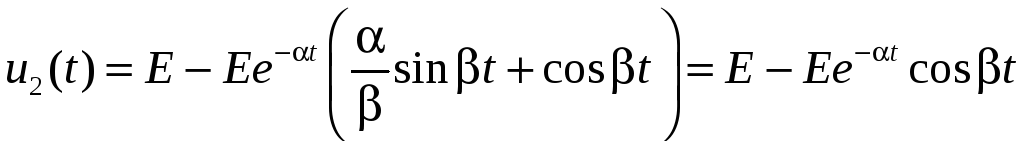 .
.
Здесь ω0 = (LC)–1 – собственная частота колебательного контура; β = (ω0 – α)1/2 – частота собственных колебаний в контуре при наличии резистивных потерь; α = R/(2L) – скорость затухания собственных колебаний в контуре, α =1/τ, где τ = 2L/R – постоянная времени контура.
6.7. Связь между дифференциальным уравнением и характеристиками электрической цепи
1) Для линейной цепи при произвольном входном сигнале х(t) связь между выходным и входным сигналом записывается в виде дифференциального уравнения
![]() .
.
2) Связь дифференциального уравнения с частотной передаточной функцией.
П
 о
определению, частотная функция есть
H(jω)=
о
определению, частотная функция есть
H(jω)=![]() .
.
Если входной сигнал гармонический
![]()
 ,
(6.1)
,
(6.1)
если цепь линейная, то выходной сигнал обязательно гармонический:
![]()
 .
(6.2)
.
(6.2)
Подставим (6.1) и (6.2) в дифференциальное уравнение
![]()
В результате получим
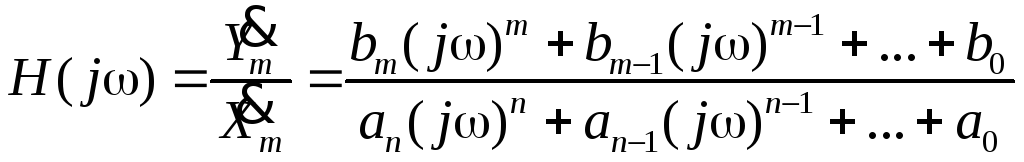 .
.
3) Связь частотной с операторной функцией цепи Н(р).
По определению, Н(р) = H(jω)|jω→p.
Отсюда
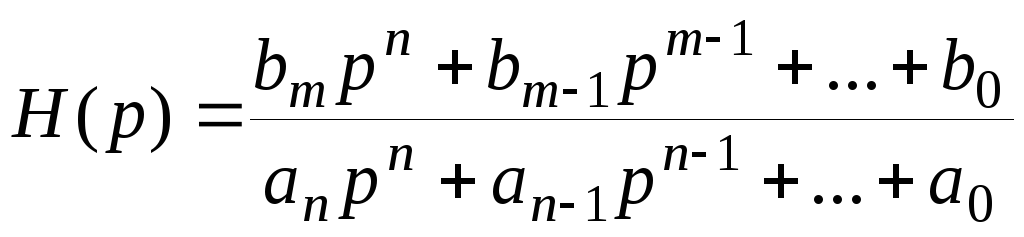 .
.
4) Связь между
импульсной и переходной характеристикой
g(t) и h(t). Так как
![]() ,
то
,
то
![]() .
.
5) Связь между g(t) и H(jω), H(p).
Из спектрального анализа следует выходной сигнал
![]() .
.
Если
![]() ,
то спектр
,
то спектр
![]() .
Следовательно,
.
Следовательно,
![]() – обратное преобразование Фурье (ОПФ).
– обратное преобразование Фурье (ОПФ).
![]() – прямое преобразование Фурье (ППФ).
– прямое преобразование Фурье (ППФ).
Таким образом, все способы описания электрической цепи связаны между собой.
Контрольные вопросы
-
с чем связано возникновение переходных процессов в электрической цепи?
-
В чем заключается классический и спектральный методы анализа линейных цепей?
-
В чем заключается суть анализа линейных цепей методом интеграла Дюамеля?
-
Каков характер переходной характеристики в цепи первого порядка?
-
Как формулируются законы коммутации?
-
Какими основными свойствами обладает единичная функция?
-
Как дифференцирующая и интегрирующая цепи влияют на импульсные сигналы?
-
На вход цепи с операторной передаточной функцией вида Ku(p) = (1+pτ)–1 воздействует гармонический сигнал s1(t)=A cos(ωt). Записать отклик.
-
В каких задачах удобен спектральный метод анализа?
-
Нарисовать схему замещения цепи (рис. 6.23) при ω→0 и ω→∞.
-
Для каких целей применяется интегрирующая цепь?
-
Как связаны между собой импульсная и переходная характеристика линейной цепи?