Резонанс в связанных колебательных контурах

П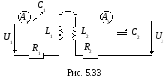ри настройке связанных колебательных контуров добиваются наибольшего значения тока I₂ во втором контуре (рис. 5.33).

При настройке нужно следить за амперметром A₂, добиваясь максимума его показаний. Настройку контуров можно вести путем изменения емкости конденсатора C₁ (при этом изменяется реактивное сопротивление контура X₁₁), емкости конденсатора C₂ (изменяется реактивное сопротивление второго контура X₂₂) и коэффициента связи K_св (изменяется сопротивление связи ).

Осуществим настройку в следующем порядке.

При разомкнутом втором контуре настроим в резонанс первый контур, т.е. получим X₁₁ = 0. При этом показание амперметра A₁ будет максимальным. Затем при «слабой» связи настроим второй контур, добившись равенства X₂₂ = 0. При этом показание амперметра A₂ будет максимальным. После этого начнем регулировать коэффициент связи, стремясь еще более увеличить ток I₂.

Для связанных контуров получили систему

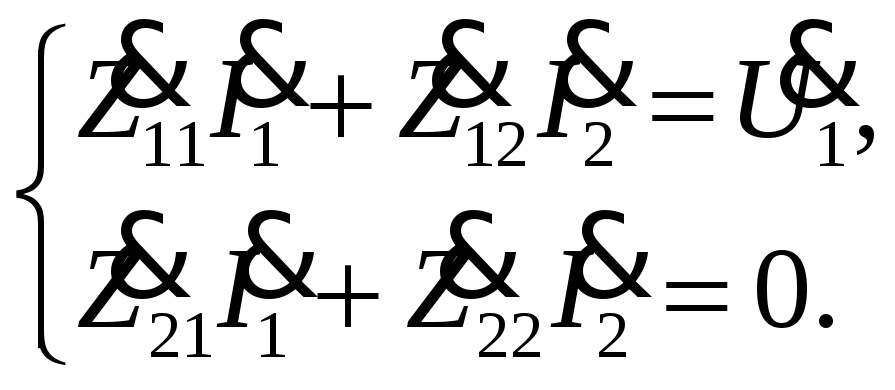
Найдем ток с учетом того, что ,

.

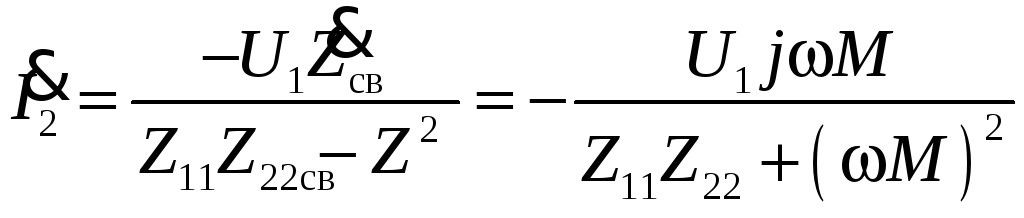
Когда оба контура настроены , то , и тогда модуль тока во втором контуре

,

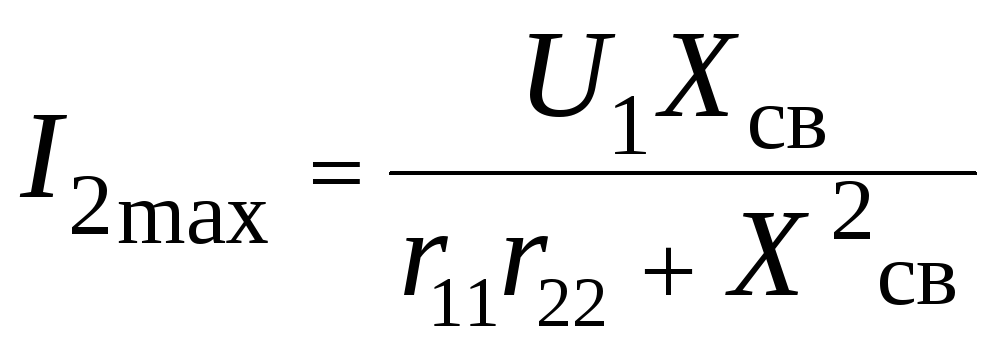
а его наибольшее значение будет иметь место при некотором значении сопротивления связи, которое называется оптимальным.

Приравняв нулю производную

,

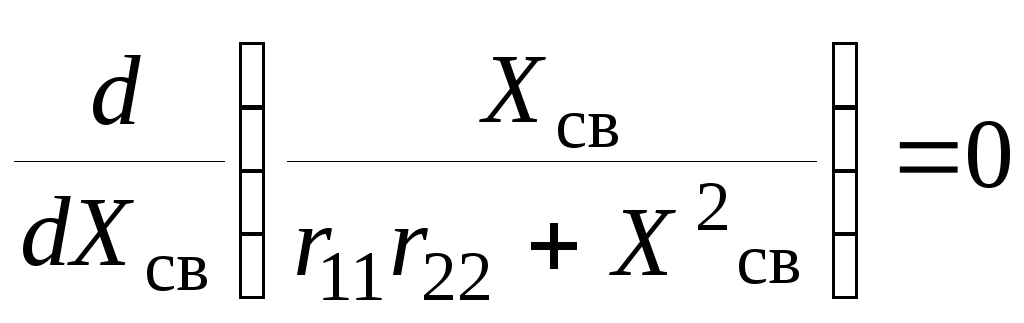найдем оптимальное сопротивление связи , тогда .

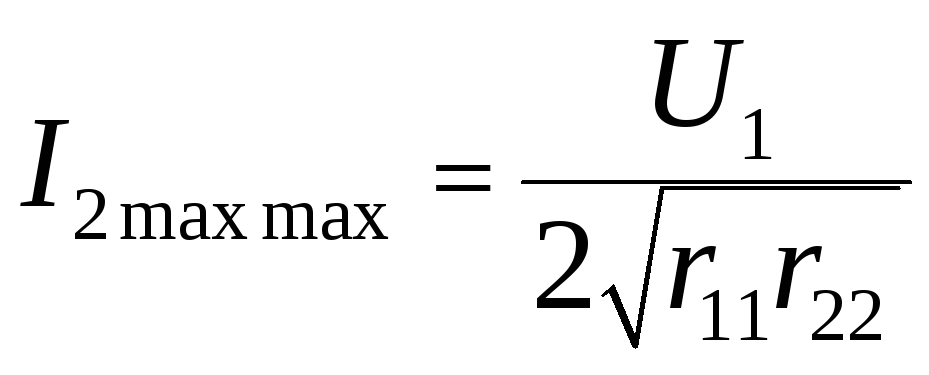Когда оба контура настроены в отдельности, а затем достигнута оптимальная связь, то говорят, что связанные контуры настроены в полный резонанс.

Если после настройки системы в полный резонанс усилить связь, то возрастут вносимые сопротивления. Теперь уже сопротивление , и во втором контуре не выделится наибольшая мощность. Однако можно вновь достичь выделения наибольшей мощности, если несколько расстроить вторичный контур. В этом случае возрастает реактивное сопротивление , что уменьшает вносимое активное сопротивление , и вновь можно добиться равенства , но уже при некоторых частотах, больших или меньших резонансной. Эти частоты называют частотами связи (и ) (рис. 5.34).

При полном резонансе оптимальный коэффициент связи

,

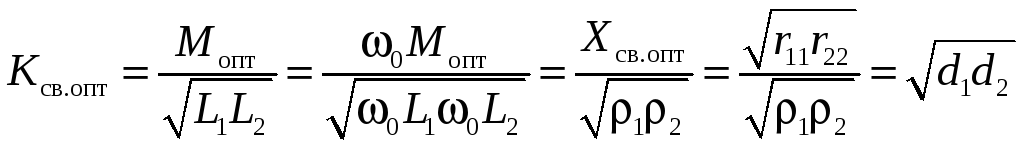где d₁ и d₂ – затухания контуров. Если связанные контуры имеют одинаковые параметры, то d₁ = d₂ и .

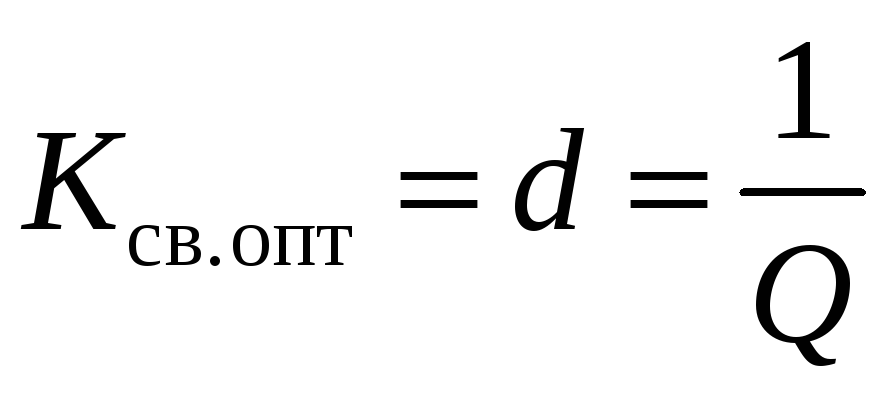При одинаковых контурах оптимальный (критический) коэффициент связи численно равен затуханию любого из связанных контуров.

Кроме полного в рассматриваемой схеме возможны еще пять резонансов.

Два сложных резонанса возникают, когда производится настройка только одного из двух контуров (первого или второго при оптимальной связи).

Индивидуальный резонанс наступает, когда оба контура настроены в отдельности, но при произвольном (не оптимальном) значении коэффициента связи.

Два частных резонанса возникают, если настраивается один из контуров при произвольной (не оптимальной) связи.

5.6. Операторные функции цепи

Ч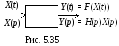астотными функциями (характеристиками) цепи удобно пользоваться, когда входные сигналы являются гармоническими или представляются их суммой. В тех случаях, когда это не выполняется, удобнее пользоваться операторным представлением сигналов, а характеристики цепей представлять их операторными функциями (рис. 5.35).

Операторная функция цепи Н(р) есть отношение операторного представления отклика цепи к операторному представлению воздействию

,

где – комплексная частота.

Названия операторных функций аналогичны названиям частотных характеристик (например, операторная функция коэффициента передачи напря-жений).

Законы Ома и Кирхгофа, когда напряжения и токи представляются их операторными представлениями, называются законами Ома и Кирхгофа в операторной форме.

– операторное сопротивление двухполюсника (рис. 5.36).

Для расчета операторной функций цепи необходимо от исходной схемы электрической цепи перейти к операторной схеме замещения, при этом сопротивление, емкость и индуктивность замещаются на операторные сопротивления, как показано на рис. 5.37.

U(p)

I(p)

Z(p)

Z_R = R

R

С

Z_С =

1

pC

L

Z_L = pL

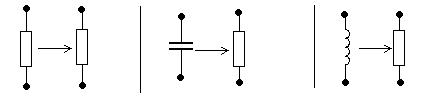
Рис. 5.36 Рис. 5.37

Для расчета операторной функции можно пользоваться всеми теми же методами, что рассматривались раньше для расчета цепей с использованием комплексных амплитуд. Подробный анализ показывает, что операторный коэффициент передачи можно получить на основе комплексного коэффициента передачи. Для этого вместо jω нужно поставить переменную р, т.е. Н(р) = Н(jω)|_jω = p. Отметим, что перед такой подстановкой комплексный коэффициент передачи нельзя подвергать каким либо преобразованиям, при которых мнимые единицы j перемножаются или сокращаются.

Если известна частотная характеристика цепи Н(jω) = Н(р), то в общем случае она представляется отношением двух полиномов

.

Корни числителя называются нулями операторной функции .

К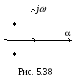орни знаменателя называются полюсами операторной функции. .

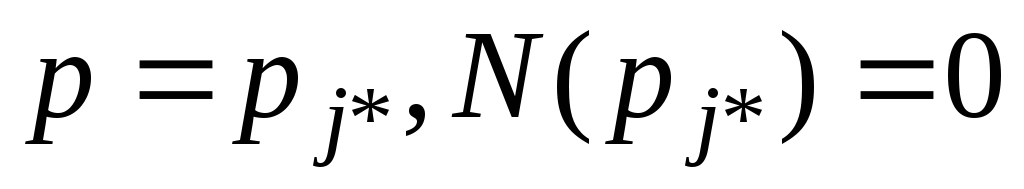Нули и полюсы изображают точками на комплексной плоскости (рис. 5.38). Такой график называют картой нулей и полюсов. Свойства операторной функции оценивают по расположению нулей и полюсов на комплексной плоскости комплексной частоты.

Контрольные вопросы

1. В чем заключается различие между откликом и воздействием?

2. Дать определение входным, выходным и передаточным параметрам четырехполюсника.

3. Как определяется частотный коэффициент передачи линейной цепи?

4. Дать понятия о годографе.

5. В чем заключается сущность амплитудного и фазового резонанса?

6. Каков фазовый сдвиг между входными напряжением и током на резонансной частоте на входе последовательного колебательного контура?

7. Как изменится добротность последовательного колебательного контура при подключении резистора параллельно с конденсатором контура?

8. Как изменится добротность последовательного колебательного контура при подключении резистора последовательно с элементами контура?

9. В каком колебательном контуре (узкополосной или широкополосной цепи) медленнее затухают собственные колебания?

10. Как называются резонансы в последовательном и параллельном колебательных контурах?