Глава 6

Импульсные сигналы в линейных цепях

В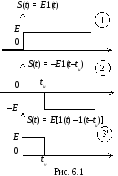 электрических цепях наряду с непрерывными сигналами, которые описываются непрерывными функциями времени, часто применяются и импульсные сигналы. Они существуют не на всей временной оси, и их величина не произвольна.

Н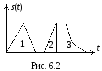азвания импульсным сигналам дают в соответствии с их формой. Основными простейшими импульсными сигналами являются сигналы, представленные на рис. 6.1: 1 – положительный перепад амплитуды Е; 2 – отрицательный перепад амплитуды Е, задержанный на t_u; 3 – одиночный прямоугольный импульс, есть сумма двух предыдущих сигналов.

Кроме перечисленных сигналов в импульсной технике широко применяются сигналы, показанные на рис. 6.2: 1 – треугольный импульс, 2 – пилообразный импульс, 3 – экспоненциальный импульс.

6.1. Временные характеристики цепей

Выделяют две временных характеристики цепей.

1. Переходная характеристика – это отклик цепи на единичное ступенчатое воздействие при нулевых начальных условиях.

2. Импульсная характеристика – это отклик цепи на воздействие сигнала в виде дельта-функции.

6.2. Понятие о переходных процессах в электрических цепях. Понятие о коммутации

Переходные (нестационарные) процессы возникают в результате коммутаций электрической цепи. Под коммутацией понимают любое скачкообразное изменение, нарушающее установившийся режим. Это различные включения и выключения как пассивных, так и активных элементов, что приводит к изменению топологии цепи или ее параметров, а также изменения параметров воздействующих сигналов. Обычно считают, что коммутация совершается мгновенно. Таким образом, мгновенное изменение входного сигнала, топологии электрической цепи или ее параметров называют коммутацией.

Переход электрической цепи из одного энергетически стационарного состояния в другое происходит не мгновенно. Время, за которое цепь переходит из одного энергетического состояния в другое, называется временем переходного процесса.

Переходной процесс связан с энергоемкими элементами, входящими в цепь. К энергоемким элементам относят емкость и индуктивность. Вследствие того что запасенная энергия является непрерывной функцией времени, ток через индуктивность и напряжение на емкости также являются непрерывными функциями времени. Этот вывод формулируется в виде законов коммутации.

Первый закон коммутации. В начальный момент времени после коммутации ток через индуктивность сохраняет такое же значение, как и непосредственно перед коммутацией: i_L(+0) = i_L(–0).

Второй закон коммутации. В начальный момент времени после коммутации напряжение на емкости сохраняет такое же значение, как и непосредственно перед коммутацией: u_C(+0) = u_C(–0).

6.3. Методы анализа линейных цепей при импульсном воздействии

Задача анализа цепи заключается в отыскании отклика при известном входном сигнале (воздействии).

При импульсном воздействии x(t) – произвольная функция времени.

При произвольном входном сигнале основными методами анализа цепей являются:

1) классический метод;

2) спектральный метод;

3) операторный метод;

4) временной (метод интеграла Дюамеля).

6.3.1. Классический метод анализа

Данный метод сводится к составлению и решению дифференциального уравнения, устанавливающего связь между откликом и воздействием. Порядок применения метода следующий.

1) составление дифференциального уравнения и приведение его к стандартному виду.

Уравнение составляется на основе законов Ома и Кирхгофа, а также с использованием метода контурных токов, узловых потенциалов и других. При составлении уравнения используют следующие соотношения:

; ; .

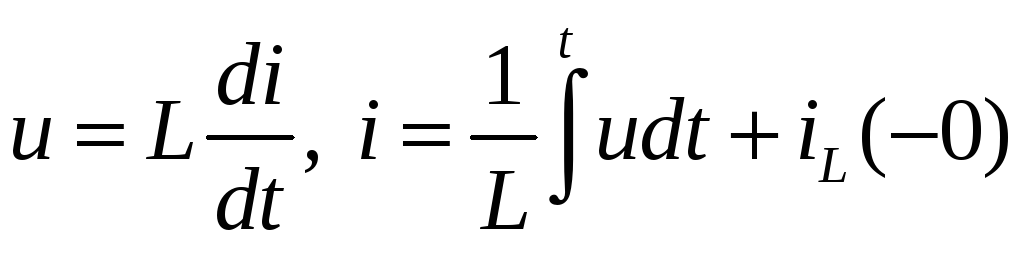При составлении уравнения за неизвестные принимают переменные состояния цепи, т.е. величины, которые отражают энергетическое состояние цепи. К ним относят u_C и i_L. Составленные уравнения цепи после преобразований, приведения подобных членов и дифференцирования сводят к неоднородному линейному уравнению.

Общий вид линейного неоднородного дифференциального уравнения (ЛНДУ):

,

где y(t) – отклик; х(t) – воздействие; a_i – постоянные, зависящие от R, L, C;

n – порядок дифференциального уравнения (ДУ). Порядок ДУ зависит от числа реактивных элементов и схемы их соединения. В простейшем случае число реактивных элементов равно n.

2) Запись общего решения ЛНДУ.

Оно состоит из суммы двух составляющих:

y(t) = y₁(t) + y₂(t).

y₁(t) – общее решение однородного линейного дифференциального уравнения, когда f = 0. Это решение не зависит от воздействия (x) и называется свободной составляющей общего решения, которое известно и равно:

,

где p_i – корни характеристического уравнения, A_i – постоянные интегрирования.

y₂(t) – это частное решение НЛДУ, оно зависит от x(t), а потому называется вынужденной составляющей общего решения.

3) Нахождение вынужденной составляющей y₂(t).

Она зависит от воздействия. Если входной сигнал имеет стационарный режим, то за частное решение принимают решение уравнения в установившемся (стационарном) режиме. При ступенчатом воздействии такой режим имеет место, когда t  . Это соответствует постоянной составляющей, т.е. гармоническому сигналу с нулевой частотой, , а потому y₂(t) находят из схемы замещения исходной цепи при  = 0.

4) Нахождение p_i.

Коэффициенты экспоненты находятся как корни характеристического уравнения, которое получают из дифференциального путем замены производных на :

.

5) Нахождение постоянных интегрирования A_i.

Постоянные интегрирования общего решения определяются из начальных условий (при t = 0) для искомой функции и ее производных:

; ; .

Конкретные значения этих функции при t = 0 находят из схем замещения исходной цепи при t = +0 с учетом законов коммутации для L, C-элементов. Если входной сигнал – ступенчатая функция, то мгновенному изменению входного сигнала при t = 0 соответствует гармонический сигнал с   , а потому искомые значения находят из схемы замещения исходной цепи при   .

6) Анализ корней характеристического уравнения и запись окончательного решения.

6.3.2. Спектральный метод анализа

Спектральный метод применяется в тех случаях, когда входной сигнал может быть представлен спектром. Сигнал имеет спектр, когда он обладает конечной энергией, т.е. удовлетворяет условию:

.

Этапы применения метода (рис. 6.3):

1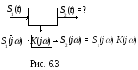) по известному сигналу находится его спектр:

– прямое преобразование Фурье;

2) по известной схеме электрической цепи определяется частотная передаточная характеристика:

;

3) находится спектральная плотность выходного сигнала:

;

4) по известному спектру выходного сигнала находится сам выходной сигнал

.

6.3.3. Операторный метод анализа

Операторный метод расчета переходных процессов применим при любых входных сигналах. Метод основан на том, что функции s(t)  вещественной переменной t, которую называют оригиналом, ставится в соответствие функция F(p) комплексной переменной p = α + j, которую называют изображением. В результате этого производные и интегралы от оригиналов заменяются алгебраическими функциями от соответствующих изображений (дифференцирование заменяется умножением на оператор р, а интегрирование – делением на него), что, в свою очередь, определяет переход от системы интегро-дифференциальных уравнений к системе алгебраических уравнений относительно изображений искомых переменных. При решении этих уравнений находятся изображения и далее путем обратного перехода – оригиналы.

Соответствие между изображением F(p) и оригиналом s(t) в сокращенной записи обозначается:

F(p) = s(t) или F(p) = L{s(t)}.

Порядок расчета переходных характеристик заключается в следующем (рис. 6.4):

1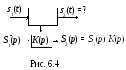) находим операторное представление входного сигнала:

– прямое преобразование Лапласа;

2) находим операторную передаточную функцию цепи:

;

3) находим операторное представление отклика:

;

4) с помощью обратного преобразования Лапласа находим отклик цепи:

.

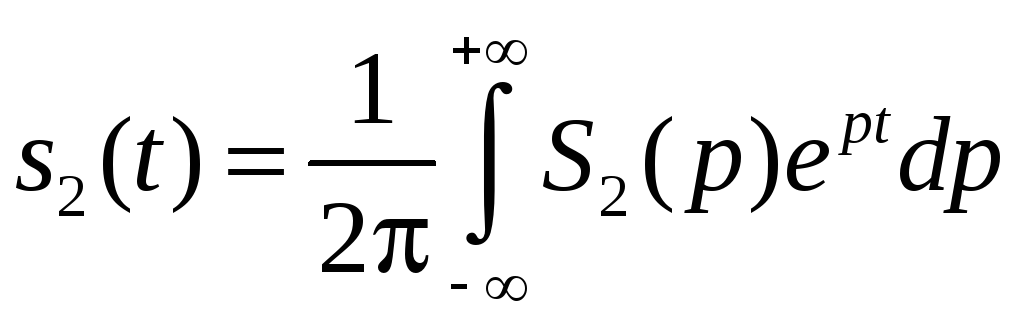Такое интегрирование является сравнительно сложным, поэтому в инженерной практике пользуются справочными таблицами.

Когда получается сложное изображение, которого нет в справочниках, то его раскладывают на более простые, используя теорему разложения L-изображения S(p).

Если изображение S(p) представлено в виде отношения двух полиномов от р, не имеющих общих корней:

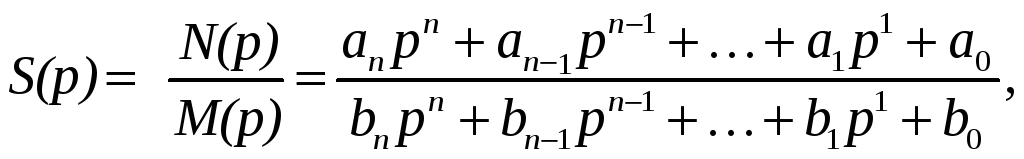
причем m > n, а уравнение M(p) = 0 не имеет кратных корней , то для перехода к оригиналу можно воспользоваться теоремой разложения

.

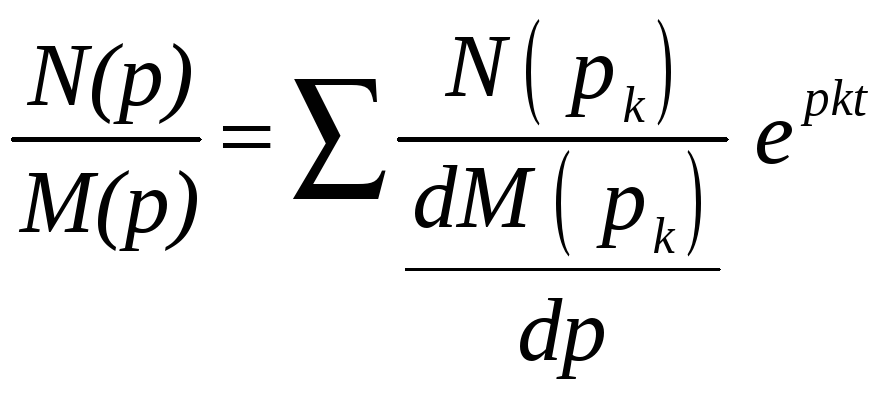
В качестве примера в таблице приведены изображения некоторых характерных функций, часто встречающихся при анализе нестационарных режимов.

 

Оригинал s(t)	А	et	sin t	cos t	sh t	ch t
Изображение S(p)

Свойства изображений.

1) Изображение суммы функций равно сумме изображений слагаемых:

.

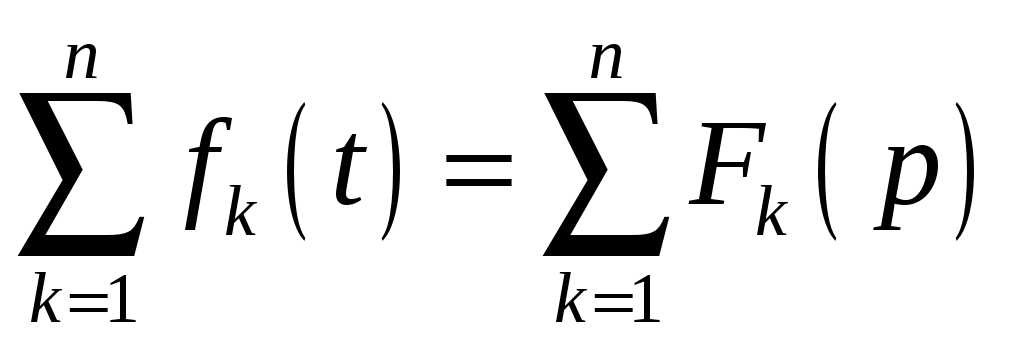
2) При умножении оригинала на коэффициент А на тот же коэффициент умножается изображение:

AF(t) = AF(p).

С использованием этих  свойств и данных таблицы, можно показать, например, что

.

Изображение для напряжения на индуктивном элементе записывается в виде

или при нулевых начальных условиях

.

Отсюда операторное сопротивление катушки индуктивности Z(p) = Lp.

С учетом ненулевых начальных условий изображение для напряжения на конденсаторе записывается:

или при нулевых начальных условиях

,

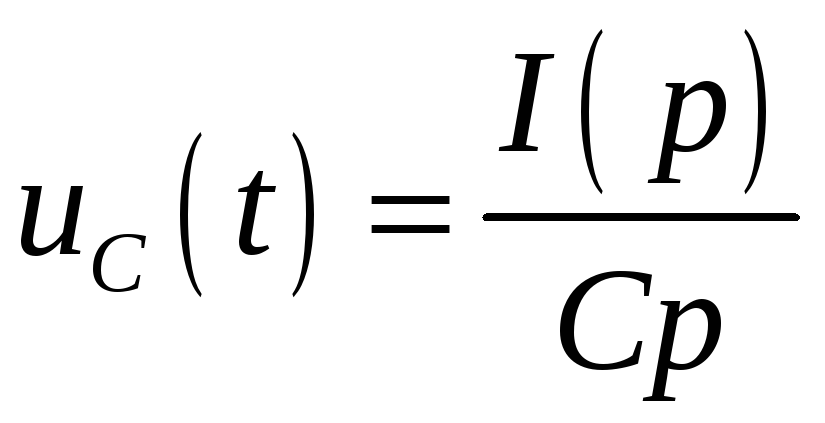
откуда операторное сопротивление конденсатора Z(p) = 1/Cp.

З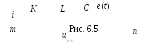акон Ома в операторной форме. Пусть имеется некоторая ветвь m – n (рис. 6.5), выделенная из некоторой сложной цепи. Замыкание ключа во внешней цепи приводит к переходному процессу, при этом начальные условия для тока в ветви и напряжения на конденсаторе в общем случае ненулевые. Для мгновенных значений переменных можно записать:

.

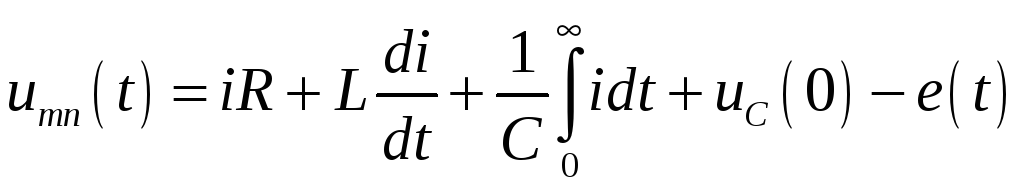Тогда на основании приведенных соотношений получим:

.

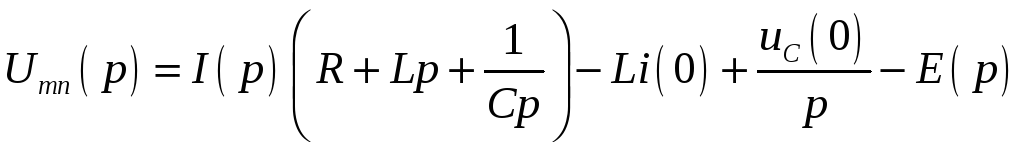Отсюда

,

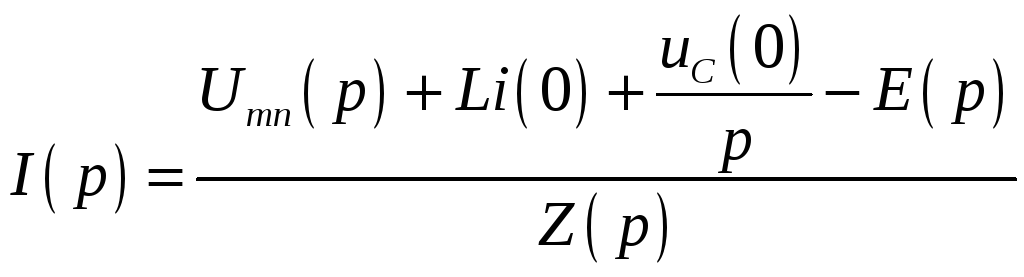где Z(p) = R + Lp + 1/Cp – операторное сопротивление рассматриваемого участка цепи.

Следует обратить внимание, что операторное сопротивление Z(p) соответствует комплексному сопротивлению Z(j) ветви в цепи синусоидального тока при замене оператора р на j.

Законы Кирхгофа в операторной форме. Первый закон Кирхгофа. Алгебраическая  сумма  изображений  токов, сходящихся в узле, равна нулю

.

Второй  закон Кирхгофа. Алгебраическая сумма изображений  ЭДС,  действующих в контуре, равна алгебраической сумме изображений напряжений на пассивных элементах этого контура:

.

При записи уравнений по второму закону Кирхгофа следует помнить о необходимости учета ненулевых начальных условий (если они имеют место). С их учетом последнее соотношение может быть переписано в развернутом виде

.

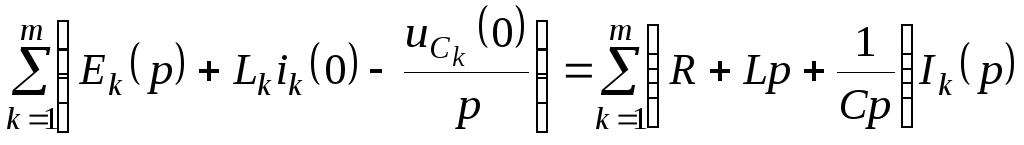В качестве примера запишем выражение для изображений токов в цепи на рис. 6.6 для двух случаев:

1) u_C(0) = 0;

2) u_C(0)  0.

В первом случае в соответствии с законом Ома

.

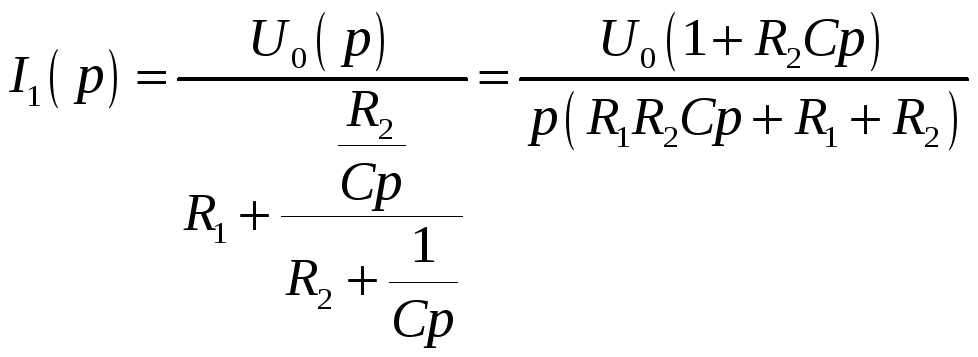Тогда

.

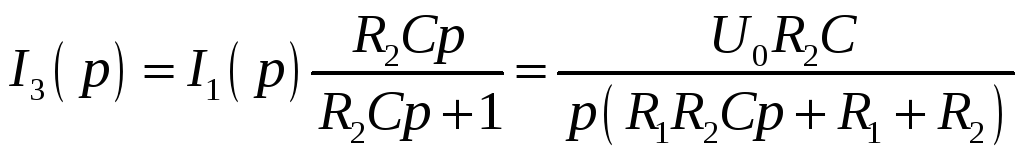Во втором случае, т.е. при u_C(0)0, для цепи на рис. 6.6 следует составить операторную схему замещения, которая приведена на рис. 6.7. Изображения токов в ней могут быть определены любым методом расчета линейных цепей, например методом контурных токов:

U₀(p)

İ₁₁(p)

İ₂₂(p)

İ₂(p)

İ₃(p)

İ₁(p)

R₂

R₁

1 Cp

u_C(0) p

U₀

R₂

R₁

i₁

i₂

i₃

C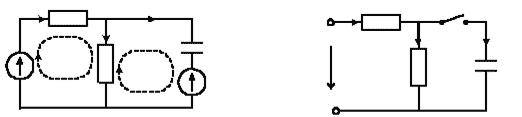

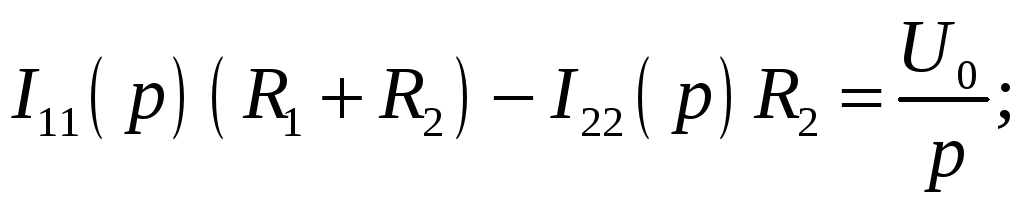
Рис. 6.6 Рис. 6.7

откуда , и .

 

6.3.4. Метод интеграла Дюамеля

Он позволяет находить отклик цепи при нулевых начальных условиях при произвольном входном сигнале и известной переходной (импульсной) характеристике цепи h(t) (рис. 6.8).

Произвольный импульсный сигнал (рис. 6.9) заменим совокупностью элементарных ступенчатых сигналов с амплитудами ∆х, возникающими в моменты времени τ_к со сдвигом по времени на .

Схема h(t)

x(t)

y(t) = ?

0

t

_к

x₀

x



x(t)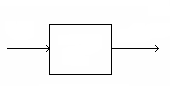

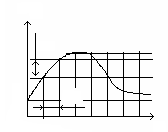
Рис. 6.8 Рис. 6.9

Как следует из рис. 6.9, х₀ – амплитуда нулевого ступенчатого сигнала. Тогда отклик на него ; – амплитуда элементарного ступенчатого сигнала, рассчитывается из выражения , где х' (τ_к) – производная от сигнала в момент времени τ_к, она равна тангенсу угла наклона сигнала в момент времени τ_к. Тогда отклик на элементарный ступенчатый сигнал .

Используя принцип суперпозиции и переходя к пределу суммы при Δτ→0 (Δτ = dτ), можно записать

.

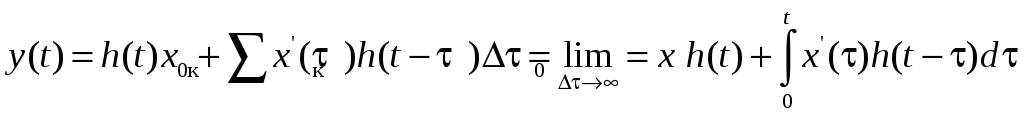Последнее выражение и называется интегралом Дюамеля. Оно позволяет получить отклик на заданное воздействие в любой момент времени t после коммутации. Интегрирование ведется по τ – текущее время (0 < τ < t), причем выражения х'(τ) и h(t – τ) получают из выражений для х(t) и h(t) путем замены t на τ и t – τ.

6.4. Передача импульсных сигналов через простейшие цепи

Электрические цепи служат для связи различных устройств между собой, при этом обычно ставится задача неискаженной передачи сигнала. В ряде случаев электрические цепи применяют для преобразования сигналов одной формы в другую.

6.4.1. Передача импульсных сигналов через дифференцирующую цепь

Цепь, состоящая из RC-элементов и приведенная на рис. 6.10, называется дифференцирующей RC-цепью.

Установим связь между выходным u₂ и входным u₁ напряжениями, считая входной сигнал u₁ произвольным.

Используя второй закон Кирхгофа и соотношения, устанавливающие связь между напряжениями и токами на элементах схемы, запишем

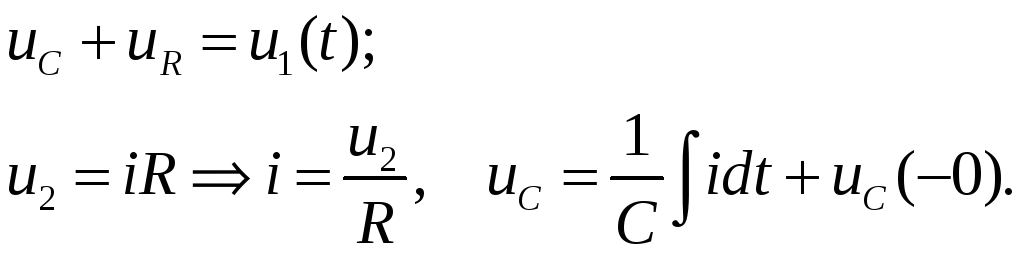
Считаем U_C(0).

Подставим полученные напряжения в первое выражение, умножим на RC и продифференцируем один раз по времени

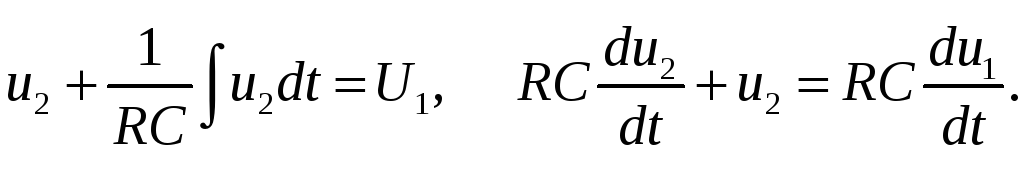
Если в этом соотношении считать, что . Последнее означает, что выходной сигнал есть производная от входного сигнала. Отсюда и название этой цепи – дифференцирующая цепь.

Рассмотрим два частных случая.

А. Пусть входной сигнал – ступенчатое напряжение амплитудой Е (рис. 6.11) . Используя классический метод, определим отклик цепи.

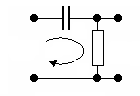
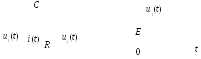
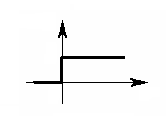
Рис. 6.10 Рис. 6.11

1) Составим дифференциальное уравнение и приведем его к стандартному виду:

.

2) Запишем общее решение

.

3) Найдем вынужденную составляющую общего решения

.

Вынужденную составляющую находим в стационарном (установившемся) режиме, который имеет место, когда t  ∞. В этом случае входной сигнал – постоянное напряжение величины , ему соответствует гармонический сигнал с нулевой частотой ω = 0, так как E = E cos ωt|_(ω=0). При таких условиях наличие индуктивности равносильно короткому замыканию (Х_L = ωL), а емкости – разрыву цепи (Х_С = (ωС)^–1).

Для нахождения вынужденной составляющей составим схему замещения исходной цепи при ω = 0 (рис. 6.12, а). Из схемы следует, что u_2(ω=0)= 0.

C

C

R

R

E

E

u_2() = 0

u₂₍₀₎ = E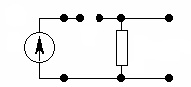

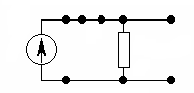
а б Рис. 6.12

4) Найдем показатель экспоненты р₁.

Коэффициенты р находят, как корни характеристического уравнения

RCр₁ + 1 = 0.

Отсюда р₁ = – (RC)^–1.

5) Найдем произвольную постоянную A₁.

Произвольные постоянные находят из начальных условий для искомой функции и ее производных (при t = +0). Значения токов и напряжений в начальный момент времени после коммутации (при t = +0) определяют из схемы замещения исходной цепи, образованной после коммутации (с учетом законов коммутации) по законам Кирхгофа. При нулевых начальных условиях наличие индуктивности равносильно разрыву цепи (i_L(–0) = i_L(+0)), а емкости – короткому замыканию (u_c(–0) = u_c(+0)).

Аналогичную схему замещения можно получить, если считать, что ступенчатому сигналу в начальный момент времени (t = +0) соответствует гармонический с бесконечно большой частотой (ω  ∞).

Для дифференцирующей RC-цепи послекоммутационная схема (при t = +0, ω  ∞) приведена на рис. 6.12, б, а произвольную постоянную A₁ находят из уравнения

=A₁=.

6) Запись общего решения:

.

Выходное напряжение представляет собой экспоненциальный импульс, который характеризуется двумя параметрами (рис. 6.13):

Рис. 6.13

1) Е – амплитуда импульса;

2) τ – постоянная времени цепи. Определим выходной сигнал при t = τ.

.

Отсюда следует, что постоянная времени – это время, за которое импульс, убывая по экспоненциальному закону, изменяется от Е до уровня 0,37Е (т.е. убывает в е = 2,71 раза).

Иногда пользуются третьим параметром: t_уст – время установления выходного напряжения, это время, за которое сигнал достигает своего стационарного значения с заданной точностью от амплитуды импульса. Так, время установления на уровне 0,1 и 0,05 составляет t_уст 0,1 = 2,3τ; t_уст 0,05 = 3τ.

Б. Пусть входной сигнал – одиночный прямоугольный импульс (рис. 6.14) амплитудой Е и длительностью t_и. Такой импульс представляет собой суперпозицию двух ступенчатых сигналов и записывается как

.

Зная отклик на ступенчатый сигнал и используя принцип суперпозиции, можно записать аналитическое выражение для выходного сигнала:

.

На рис 6.15 показаны три временные диаграммы выходного сигнала при различных соотношения между τ и t_и.

E

u₁

t

E

E

E

–E

–E

–E

t

t

t

u₁

u₁

u₁

u₂

u₂

u₂

t_и

t_и

t_и

<< t_и

 >>t_и

 ~ t_и

а

б

в

t_и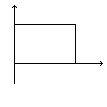

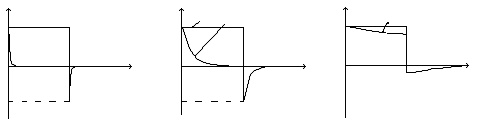
Рис. 6.14 Рис. 6.15

В зависимости от соотношения между τ и t_и эта схема имеет три названия.

Если τ << t_и, то цепь называется дифференцирующей RC-цепью (рис. 6.15, а).

Если τ ≈ t_и, то цепь называется укорачивающей RC-цепью (рис. 6.15, б).

Если τ >> t_и, то цепь называется разделительной RC-цепью (рис. 6.16, в).

Рассмотрим процессы, протекающие в цепи при воздействии на вход прямоугольного импульса при нулевых начальных условиях u_c(–0) = 0.

Напряжения на элементах связаны вторым законом Кирхгофа

u₁ = u_c + u_R.

При t < 0 u₁ = 0, u_c = 0, следовательно, u_R = 0. Это исходное состояние.

При t = +0 u₁ = Е, u_c = 0, E = 0 + u_R. Следовательно, u_R = Е. Это – послекоммутационное состояние цепи.

При t > 0 E = u_c + u_R. Происходит заряд конденсатора.

С током i_зар заряда напряжение на нем возрастает, а на резисторе (на выходе) убывает от Е к нулю.

При t = t_и–0 E = u_C(tи),+ u_R(tи),. К моменту окончания импульса u_c = u_c(tи), u_R = Е – u_c(tи).

При t > t_и+0 u₁ = 0 = u_c + u_R.. Следовательно, u_R = –u_c. Поэтому знак выходного напряжения меняется на противоположный.

u1(t) i(t) R L u2(t)

Рис. 6.16

При t > t_и u₁ = 0 , u_R = –u_c. Происходит разряд конденсатора С током i_разр разряда, напряжение на нем убывает, убывает и напряжение на резисторе (на выходе) от –u_c(tи) к нулю.

Цепь, состоящая из RL-элементов (рис 6.16), выполняет аналогичные преобразования над входными сигналами и называется дифференцирующей RL-цепью.