
- •Глава 5
- •5.5.1. Последовательный колебательный контур
- •Резонансная характеристика последовательного колебательного контура
- •Резонанс в связанных колебательных контурах
- •5.6. Операторные функции цепи
- •Глава 6
- •6.4.2. Передача импульсных сигналов через интегрирующую цепь
- •4) Найдем показатели экспоненты р1 и p2.
- •6.6. Расчет переходных характеристик последовательного колебательного контура
Глава 5
Частотные характеристики и операторные функции электрических цепей
Большинство электрических цепей служат средством связи для передачи сигналов от источника сигнала в нагрузку (рис. 5.1), где x(t) – сигнал на входе цепи. Он называется входным сигналом, или воздействием; y(t) – выходной сигнал, или отклик:
y(t) = F(x(t), a, b, c).
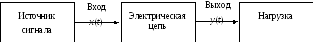
Рис. 5.1
В общем случае связь между откликом и воздействием имеет вид дифференциального уравнения. Если цепь линейная, то уравнение линейное, где a, b, c – параметры элементов, входящих в цепь.
Если входной сигнал гармонический, то его представляют комплексной амплитудой.
![]() →
→
![]() .
.
Если цепь линейная,
то откликом такой цепи является
гармонический сигнал с комплексной
амплитудой
![]()
![]()
![]() .
.
Причем связь между комплексной амплитуды отклика и воздействия имеет вид линейного алгебраического уравнения:
![]() ,
,
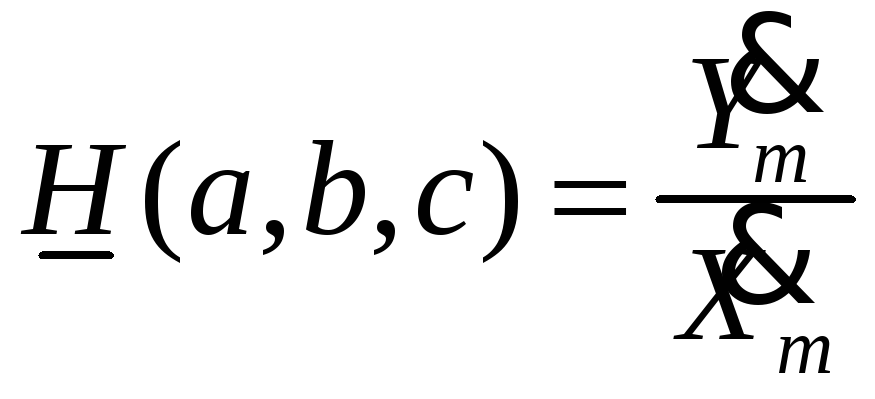 ,
,
где H (a, b, c) – параметр электрической цепи (это комплексное число).
Параметр цепи есть отношение комплексной амплитуды отклика к комп-лексной амплитуде воздействия.
5.1. Параметры двухполюсника
Двухполюсником
является цепь с двумя выводами рис. 5.2.
Его режим работы характеризуется двумя
величинами
![]()
1. Если воздействием считать амплитуду тока, то откликом будет являться напряжение на нем.
По закону Ома:
![]() ,
где Z – сопротивление
двухполюсника. (Z = R+jX
– комплексное число, где R
и X – резистивная и
реактивная составляющие сопротивления
двухполюсника).
,
где Z – сопротивление
двухполюсника. (Z = R+jX
– комплексное число, где R
и X – резистивная и
реактивная составляющие сопротивления
двухполюсника).
Обобщенная схема замещения двухполюсника приведена на рис. 5.3.
2. Если воздействием считаем амплитуду напряжения, тогда откликом будет амплитуда тока, связанная с напряжением:
![]() ;
;
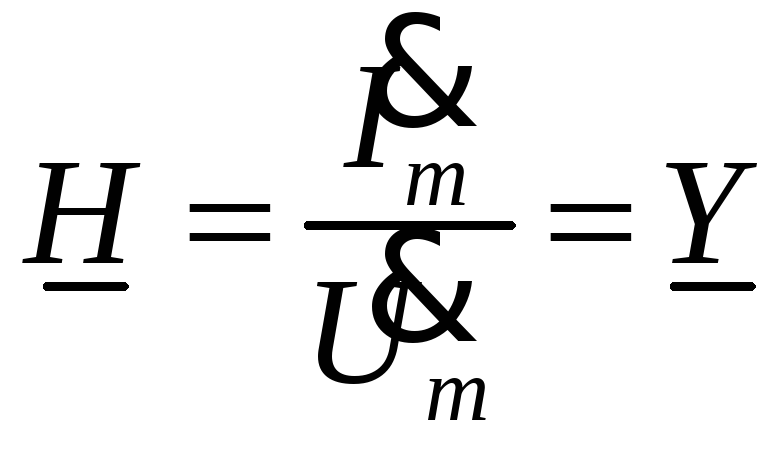 ,
,
г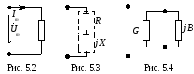 де
Y – второй параметр
двухполюсника, он называется комплексной
проводимостью двухполюсника:
де
Y – второй параметр
двухполюсника, он называется комплексной
проводимостью двухполюсника:
Y = G + jB,
G и B – резистивная и реактивная составляющие проводимости двухполюсника.
Вторая схема замещения двухполюсника приведена на рис. 5.4. Эти схемы замещения при определенном выборе параметров эквивалентны.
5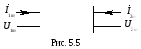 .2.
Параметры четырехполюсника
.2.
Параметры четырехполюсника
Четырехполюсник – это цепь с четырьмя выводами (рис. 5.5).
Параметры четырехполюсника можно разбить на четыре группы:
1.
Входные параметры связывают
![]() и
и
![]() :
:
По отношению к источнику сигнала четырехполюсник является двухполюсником, а поэтому его входные параметры аналогичны параметрам двухполюсника:
 ,
,
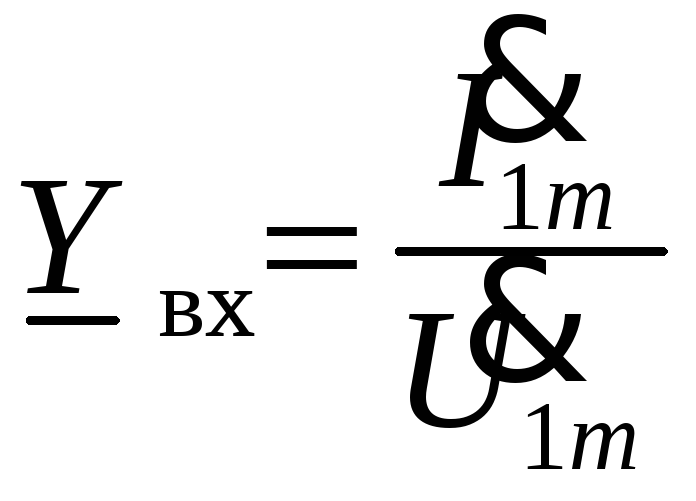 ,
,
где Zвх – входное сопротивление четырехполюсника; Yвх – входная проводимость четырехполюсника.
2. Передаточные параметры характеризуют передачу сигнала с входа на выход, или, как говорят, передачу в прямом направлении. Передаточных параметров четыре
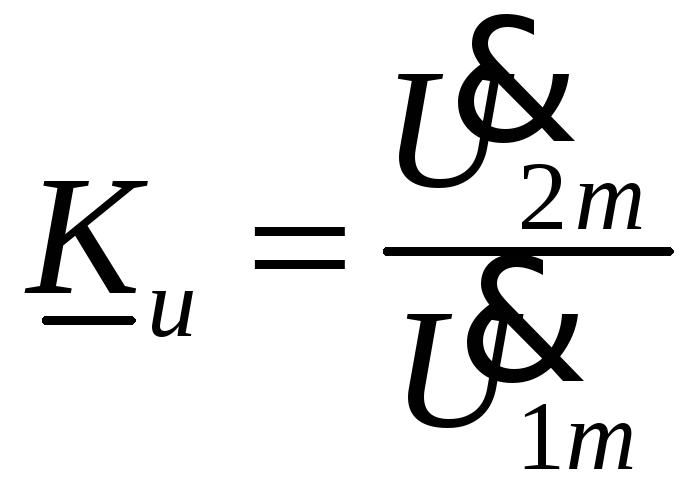 ;
;
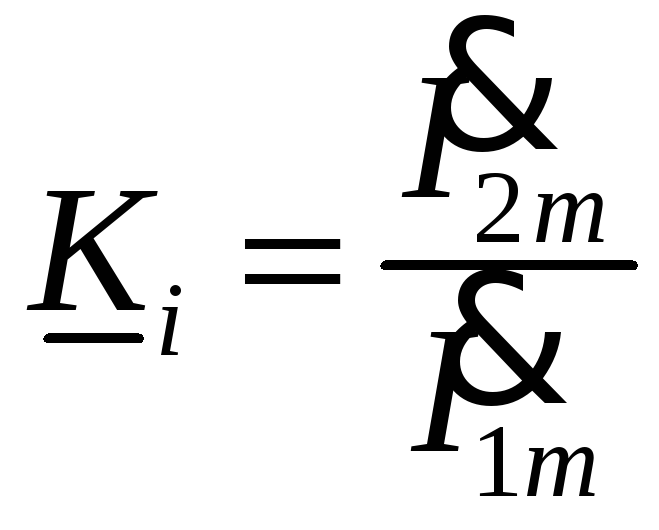 ;
;
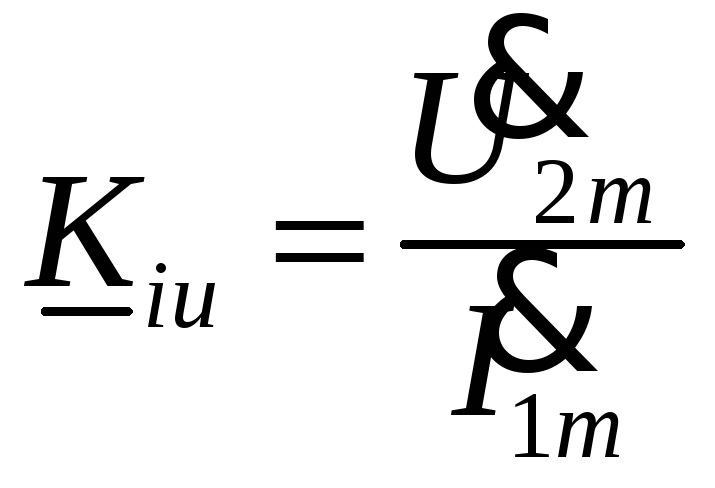 ;
;
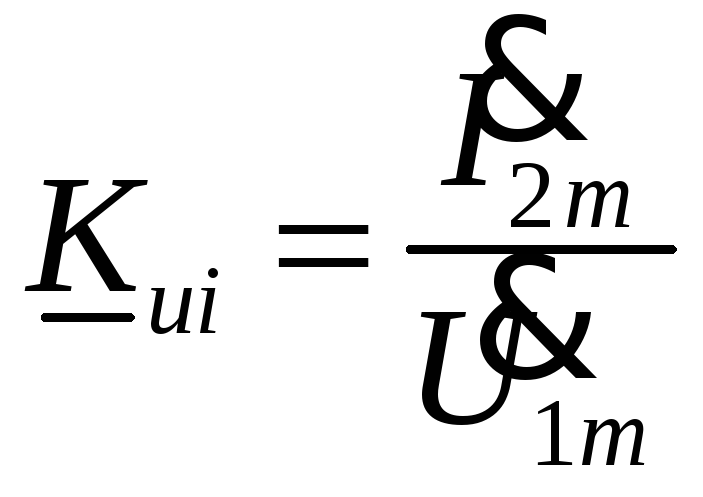 ,
,
где Ku – коэффициент передачи по напряжению;
Ki – коэффициент передачи по току;
Kiu – сопротивление прямой передачи, или коэффициент преобразования ток – напряжение;
Kui – проводимость прямой передачи, или коэффициент преобразования напряжение – ток.
3. Выходные параметры:
а) Zвых = 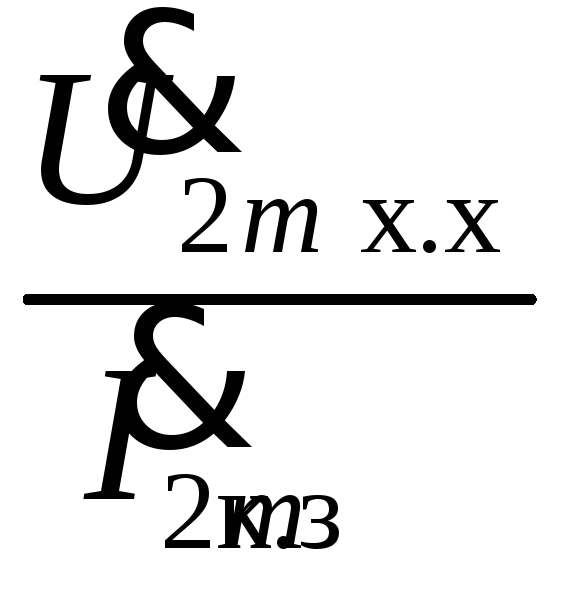 ,
,
где Zвых – комплексное выходное сопротивление;
![]() –
комплексная амплитуда выходного
напряжения в режиме холостого хода
(х.х). Холостой ход – это режим, когда
выполняются условия: İ2m = 0,
Zн = ∞;
–
комплексная амплитуда выходного
напряжения в режиме холостого хода
(х.х). Холостой ход – это режим, когда
выполняются условия: İ2m = 0,
Zн = ∞;
![]() – комплексная амплитуда выходного тока
в режиме короткого замыкания (к.з).
Короткое замыкание – это режим, когда
Zн = 0.
– комплексная амплитуда выходного тока
в режиме короткого замыкания (к.з).
Короткое замыкание – это режим, когда
Zн = 0.
б)
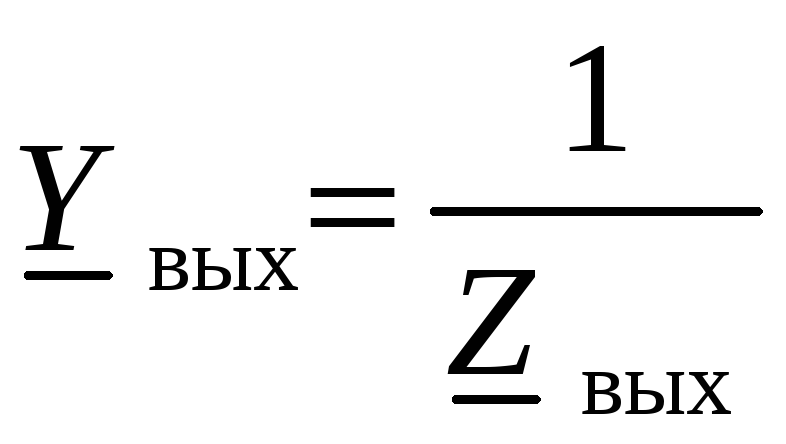 – комплексная выходная проводимость.
– комплексная выходная проводимость.
4. Параметры обратной передачи сигнала. Они характеризуют передачу сигнала с выхода на вход. Таких параметра четыре, и они аналогичны параметрам второй группы: (Ku, Ki, Kiu, Kui).
5.3. Частотные характеристики
Поскольку сопротивления элементов цепей зависят от частоты, то параметры цепей оказываются частотно-зависимыми. Зависимости параметров цепей от частоты называют частотными характеристиками (ЧХ), или частотными функциями цепи.
Каждый параметр цепи имеет свою частотную характеристику. Название ЧХ дают в соответствии с названием параметра, например ЧХ входного сопротивления, ЧХ коэффициента передачи напряжения.
ЧХ есть зависимость от частоты отношения комплексной амплитуды отклика к комплексной амплитуде воздействия. Как всякую комплексную функцию ее можно записать в одной из трех форм записи: показательной, алгебраической и тригонометрической (применяется редко).
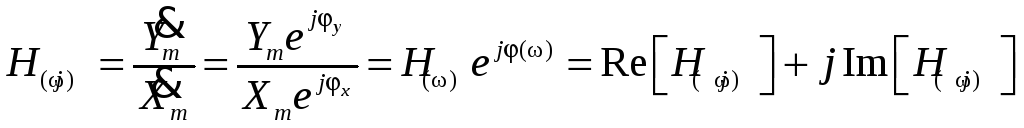 .
.
H(ω) = Ym/Xm – амплитудно-частотная характеристика (АЧХ), или ее называют модуль комплексной функции:
mod
[H(jω)] = H() =
=![]() .
.
АЧХ есть зависимость от частоты отношения амплитуды гармонического сигнала на выходе к амплитуде гармонического сигнала на входе (без учета начальных фаз).
() = y – x
– фазо-частотная характеристика (ФЧХ),
или ее называют аргументом комплексной
функции – arg[H(jω)]
=
![]() .
.
ФЧХ есть зависимость от частоты сдвига по фазе между выходным и входным сигналами.
![]() ,
,![]() – реальная и мнимая составляющие ЧХ
электрической цепи.
– реальная и мнимая составляющие ЧХ
электрической цепи.
Для наглядности ЧХ цепей представляют в графическом виде. Графики строят двумя способами.
1. Виде двух графиков – АЧХ и ФЧХ.
При построении графиков АЧХ и ФЧХ пользуются следующими масштабами по осям: линейным и логарифмическим. На рис. 5.6, а приведен график в линейном масштабе, на рис. 5.6, б – в полулогарифмическом масштабе, а на рис. 5.6, в – в логарифмическом масштабе.
H() H() lgH() 105
106
105 105 5 0
1 2 3 4 5 6 lg
0
1 2 3 4 5 6 lg
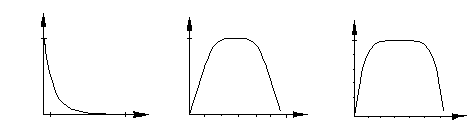
а б в Рис. 5.6
2. В виде графика функции, построенного на комплексной плоскости координат, который называют годографом. Годограф – это геометрическое место точек, которые описывает конец вектора комплексной функции на комплексной плоскости при изменении частоты от 0 до бесконечности.
Д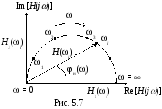 ля
построения годографа обычно используют
алгебраическую форму записи частотной
характеристики Н(jω) =
= Re[Н(jω)]
+ j Im[Н(jω)].
Далее для определенных частот ωi
рассчитывают значения Re[Н(jω)]
= Н1(ωi)
и Im[Н(jω)]
= Н2(ωi)
и составляют таблицу данных для построения
АФХ, а затем, как обычно, наносят эти
точки на плоскость и, соединив их,
получают график годографа (рис. 5.7).
ля
построения годографа обычно используют
алгебраическую форму записи частотной
характеристики Н(jω) =
= Re[Н(jω)]
+ j Im[Н(jω)].
Далее для определенных частот ωi
рассчитывают значения Re[Н(jω)]
= Н1(ωi)
и Im[Н(jω)]
= Н2(ωi)
и составляют таблицу данных для построения
АФХ, а затем, как обычно, наносят эти
точки на плоскость и, соединив их,
получают график годографа (рис. 5.7).
|
Частота f, Гц |
Re[Н(jω)] = Н1(ωi) |
Im[Н(jω)] = Н2(ωi) |
|
|
|
|
5.4. Примеры расчета частотных характеристик цепей
Пример 1. Для обобщенной одноконтурной цепи, представленной комплексной схемой замещения (рис. 5.8), рассчитать ее частотные характеристики:
Z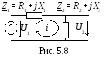 вх(j),
Zвх(),
Z();
вх(j),
Zвх(),
Z();
K(j), K(), K().
Решение.
По определению Zвх(j) = ![]() .
Используя законы Ома и Кирхгофа, найдем
КЧХ, а также АЧХ и ФЧХ входного
сопротивления:
.
Используя законы Ома и Кирхгофа, найдем
КЧХ, а также АЧХ и ФЧХ входного
сопротивления:
Z


 вх(j) = U1m/I1m =
I1m(Z1 + Z2);
I1m
= (R1+R2) + j(X1+X2) = R + jX;
вх(j) = U1m/I1m =
I1m(Z1 + Z2);
I1m
= (R1+R2) + j(X1+X2) = R + jX;
![]()
 ;
;
![]()
Используя определение K(j) и законы Ома и Кирхгофа, найдем КЧХ, а также АЧХ и ФЧХ коэффициента передачи по напряжению:
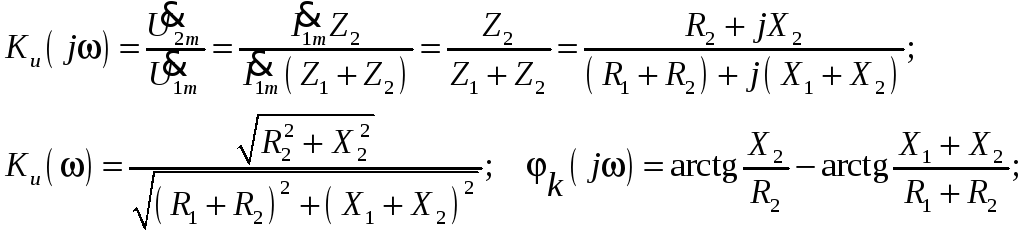
П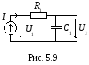 ример
2. Для цепи, изображенной на рис. 5.9,
рассчитать:
ример
2. Для цепи, изображенной на рис. 5.9,
рассчитать:
zвх(j), z(), z();
Ku(j), K(), K().
От исходной цепи переходим к ее комплексной схеме замещения. Она соответствует схеме на рис. 5.8.
Используя определение zвх(j) и законы Ома и Кирхгофа, получим его выражение
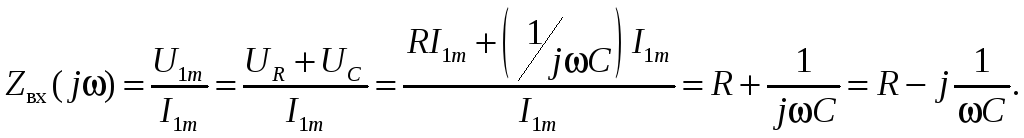
О пределим
АЧХ и ФЧХ для zвх(j)
и построим их графики (рис. 5.10), подсчитав
значения при = 0,
= :
пределим
АЧХ и ФЧХ для zвх(j)
и построим их графики (рис. 5.10), подсчитав
значения при = 0,
= :
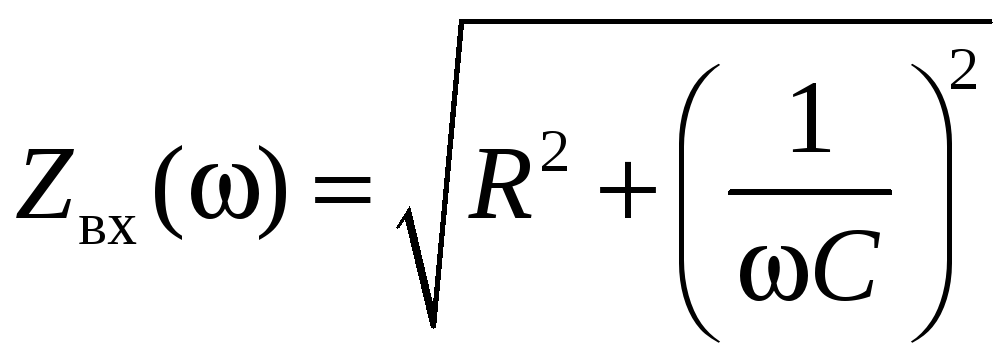 ;
Zвх(0) = ;
Zвх()
= R.
;
Zвх(0) = ;
Zвх()
= R.
z()
= – arctg
![]() ;
z(0)
= –/2; z()
= 0.
;
z(0)
= –/2; z()
= 0.
Используя определение Ku(j), получим его выражение
Ku(j)=![]() =
=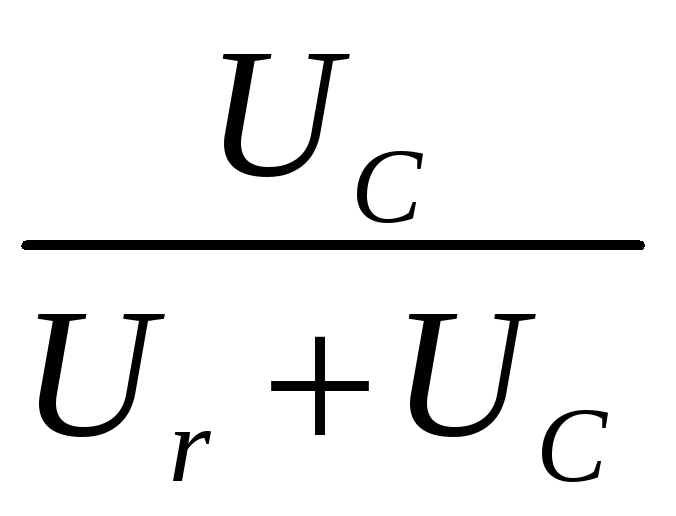 =
=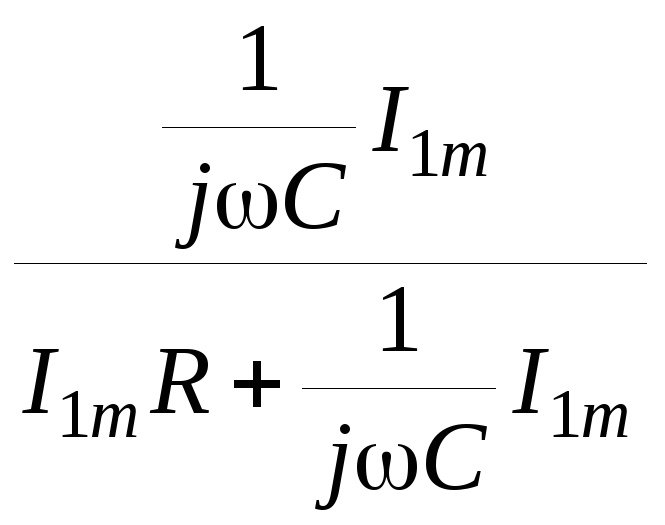 =
=![]() .
.
Определим АЧХ и ФЧХ для Ku(j) и построим их графики (рис. 5.11), подсчитав значения при = 0, = .
 Учитывая,
что
Учитывая,
что
Z =
![]() =
=
![]()
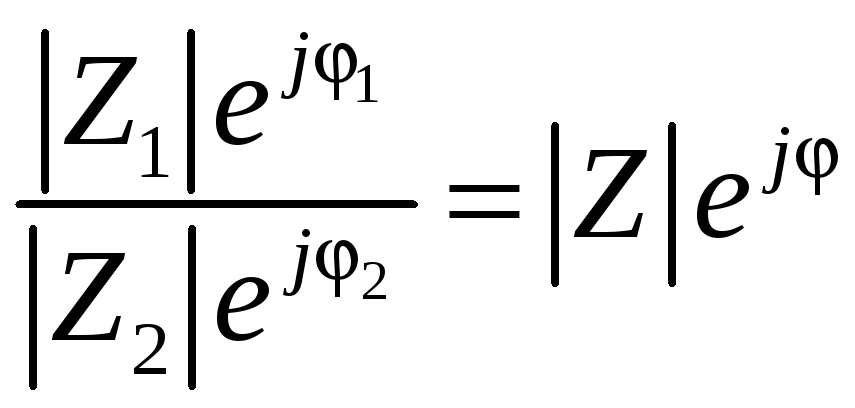 ,
,
где
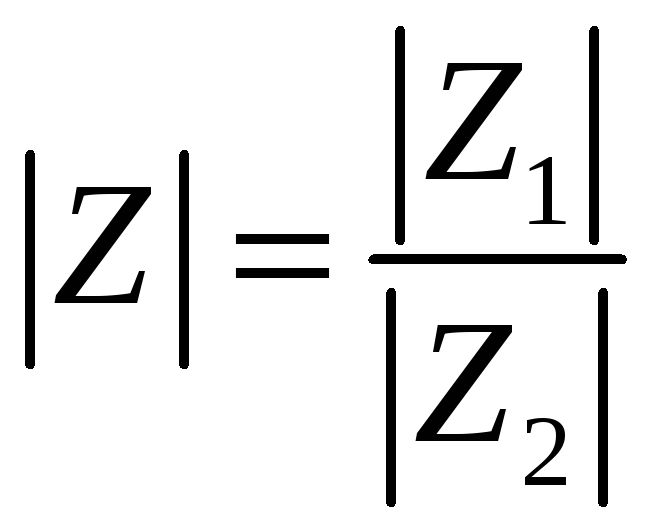 ,
,
![]() .
Тогда
.
Тогда
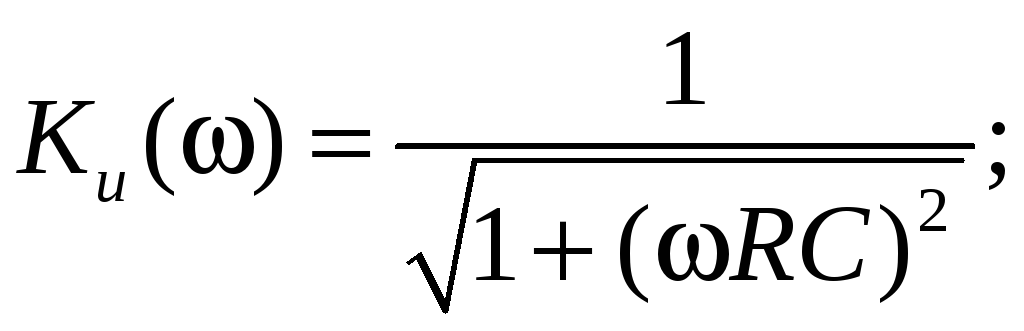 Ku(0) = 1; Ku() = 0.
Ku(0) = 1; Ku() = 0.
![]() .
.
Отсюда следует
φK() = π/2, φK(0) = 0.
Такая цепь пропускает сигналы низких частот (Ku(0) = 1) и подавляет сигналы высоких частот (Ku() = 0). Она называется фильтром низких частот (ФНЧ).
Граничная
частота определяется из выражения
![]() .
Рассчитаем ее для нашего примера:
.
Рассчитаем ее для нашего примера:
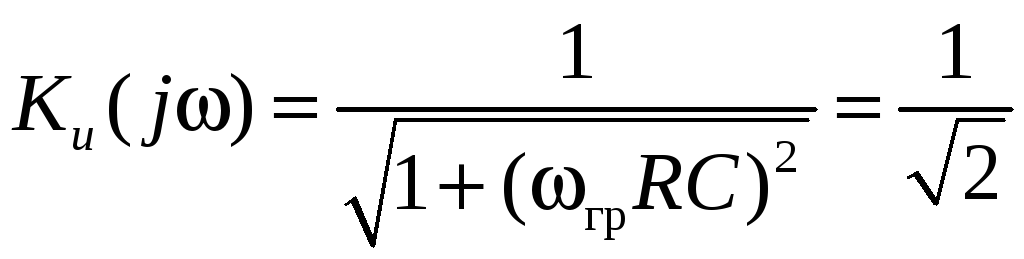 ;
грRC =1
;
грRC =1
![]() .
Построить годограф частотно-передаточной
функции (годограф иногда называют АФЧХ).
.
Построить годограф частотно-передаточной
функции (годограф иногда называют АФЧХ).
П ри
ри
![]()
![]() .
.
При
![]()
![]() .
.
Учитывая, что реальная часть всегда положительна и уменьшается от 1 до 0, а мнимая часть всегда отрицательна, можно построить график годографа (рис. 5.12).
Пример 3. Для обобщенной двухконтурной цепи, представленной комплексной схемой замещения (рис. 5.13), рассчитать ее частотные характерис-тики:
Z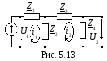 вх(j),
Zвх(),
z(),
K(j), K(),
K().
вх(j),
Zвх(),
z(),
K(j), K(),
K().
Решение. Найдем КЧХ, а также АЧХ и ФЧХ входного сопротивления.
По определению,
Zвх(j) = ![]() .
Входное сопротивление находим методом
последовательных эквивалентных
преобразований. Этот метод состоит
в поэтапном преобразовании простых
участков цепи. Они показаны на рис. 5.14.
.
Входное сопротивление находим методом
последовательных эквивалентных
преобразований. Этот метод состоит
в поэтапном преобразовании простых
участков цепи. Они показаны на рис. 5.14.
U1 U2 Z1 Z2 Z34 U1 U2 U2 U1 Z1 Z234 Z1234
н

 айдем
КЧХ коэффициента передачи по напряжению.
По определению, Ku(j) = U2m/U1m,
а U2m = Z4İ2
находим по закону Ома.
айдем
КЧХ коэффициента передачи по напряжению.
По определению, Ku(j) = U2m/U1m,
а U2m = Z4İ2
находим по закону Ома.
Отсюда видно, что для расчета КЧХ необходимо найти İ2. Находим İ2 методом контурных токов. Для этого определим число независимых контуров: Nk = b – у + 1 = 3 – 2 + 1 = 2, каждому из них присвоим свой контурный ток İ1, İ2 и составим уравнения по методу контурных токов.
Z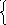

 11İ1 + Z12İ2 = E11;
Z21İ1 + Z22İ2 = E22
,
11İ1 + Z12İ2 = E11;
Z21İ1 + Z22İ2 = E22
,
где Z11 – собственное сопротивление первого контура, Z11 = Z1+Z2;
Z12 и Z21 – сопротивление смежных контуров, Z12 = Z21 = –Z2;
Z 22
– собственное сопротивление второго
контура, Z22 = Z2+Z3+Z4;
22
– собственное сопротивление второго
контура, Z22 = Z2+Z3+Z4;
Ė11 – алгебраическая сумма источников ЭДС первого контура, Ė11 = U1m;
Ė22 – алгебраическая сумма источников ЭДС второго контура, во втором контуре источников ЭДС нет, Ė22 = 0.
Найдем İ2 – ток второго контура (по методу Крамера), а затем и КЧХ коэффициента передачи по напряжению:
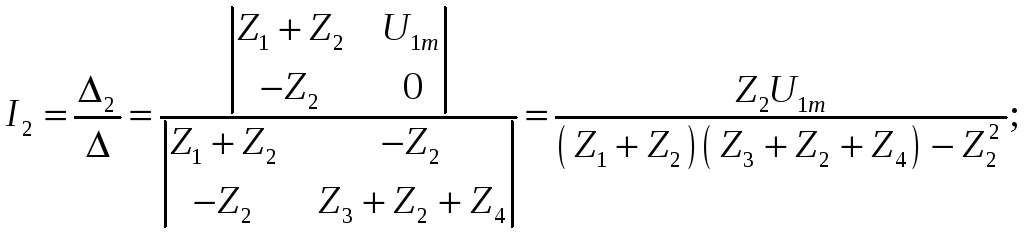


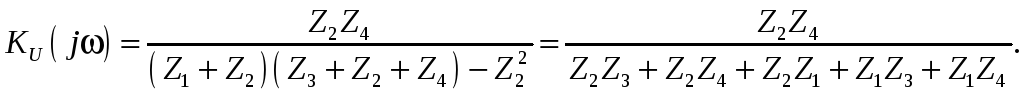
Покажем другой способ нахождения КЧХ коэффициента передачи по напряжению. Найдем КЧХ, используя для расчета U2m метод узловых потенциалов. Для этого:
-
преобразуем исходную схему к виду, показанному на рис. 5.15, заменив источник ЭДС на источник тока;
-
п
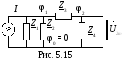 отенциал
узла 0 примем равным нулю, 0 = 0.
отенциал
узла 0 примем равным нулю, 0 = 0.
Т огда
U2m= 2
– 0 = 2.
огда
U2m= 2
– 0 = 2.
Составив уравнения по методу узловых потенциалов, получим систему второго порядка и решим ее относительно 2 по методу Крамера:
Y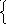 111
+ Y122
= İ11;
Y211
+ Y222
= İ22,
111
+ Y122
= İ11;
Y211
+ Y222
= İ22,
где Y11 – собственная проводимость первого узла, Y11 = (1/Z1)+(1/Z2)+(1/Z3);
Y12 и Y12 – межузловая проводимость Y12 = Y21 = –1/Z3;
Y22 – собственная проводимость второго узла Y22 = (1/Z3) + (1/Z4);
1, 2 – потенциалы первого и второго узлов;
İ11, İ22 – токи источников токов, сходящихся в первом и втором узлах.


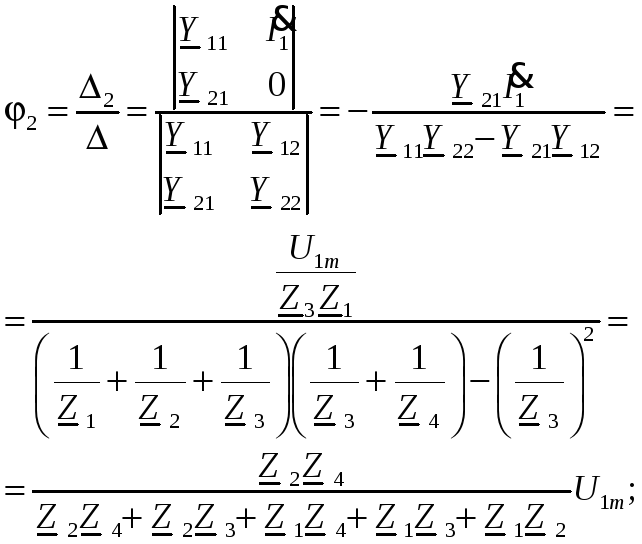
Отсюда следует, что
K
 u(j)
= U2m/U1m
= Z2 Z4/(Z2
Z4 + Z2 Z3
+ Z1 Z2 + Z1
Z3 + Z1 Z4).
u(j)
= U2m/U1m
= Z2 Z4/(Z2
Z4 + Z2 Z3
+ Z1 Z2 + Z1
Z3 + Z1 Z4).
Д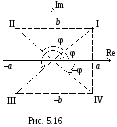 ля
построения ФЧХ необходимо пользоваться
следующими формулами:
ля
построения ФЧХ необходимо пользоваться
следующими формулами:
![]() ,
где a – реальная часть,
а b – мнимая (рис. 5.16).
ΦZ =
,
где a – реальная часть,
а b – мнимая (рис. 5.16).
ΦZ =
![]()
I
![]() a > 0,
b > 0;
φ = arctg
a > 0,
b > 0;
φ = arctg![]() ;
;
II
![]() a < 0,
b > 0;
φ =
a < 0,
b > 0;
φ =
![]() –
arctg
–
arctg![]() ;
;
III
![]() a <
0, b <
0; φ =
a <
0, b <
0; φ =
![]() +
arctg
+
arctg![]() ;
;
IV
![]() a > 0,
b < 0;
φ = –
arctg
a > 0,
b < 0;
φ = –
arctg![]() .
.
5.5. Резонансные цепи. Колебательные контуры
Явление резкого возрастания амплитуды отклика при приближении частоты внешнего воздействия к определенному значению частоты называется резонансом. Такой резонанс имеет место в механике и называется амплитудным резонансом. Частота, на которой выполняется условие резонанса, называется резонансной частотой.
В электротехнике величины, характеризующие режим работы цепи на разных элементах, имеют амплитудный резонанс на разных, хотя и близких частотах. Поэтому в теории цепей под резонансом понимают фазовый резонанс. Под фазовым резонансом понимают условие, при котором цепь, содержащая реактивные элементы (L и C), имеет входное сопротивление резистивное, т.е. при резонансе ток и напряжение находятся в одной фазе, как и на любом резистивном элементе, а сдвиг по фазе равен нулю.
Электрические цепи, в которых имеет место явление резонанса, называются резонансными. Поскольку переходные характеристики резонансных цепей имеют колебательный характер, то резонансные цепи называют колебательными контурами.
Колебательные контуры используются для решения задач частотной избирательности. Под частотной избирательностью понимают способность цепи выделять сигналы узкого диапазона частот. К простейшим колебательным контурам относят последовательный и параллельный колебательный контур, также систему связанных контуров.
