
Определители и их свойства.
Квадратной
матрице 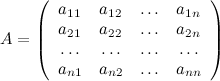
![]() -го
порядка ставиться в соответствие число
-го
порядка ставиться в соответствие число ,
называемое определителем
матрицы или детерминантом.
,
называемое определителем
матрицы или детерминантом.
Свойства определителей:
Замечание
Все что будет сказано относительно строк, будет относиться и к столбцам.
1.
При транспонировании квадратной
матрицы её определитель не меняется: ![]()
Пример
Известно, что
определитель матрицы ![]() равен
3. Тогда определитель матрицы
равен
3. Тогда определитель матрицы ![]() ,
которая равна
,
которая равна ![]() ,
также равен 3.
,
также равен 3.
2. Общий множитель в строке можно выносить за знак определителя.
Пример
![]()
3. ![]()
То есть, если квадратная
матрица ![]()
![]() -го
порядка умножается
на некоторое ненулевое число
-го
порядка умножается
на некоторое ненулевое число ![]() ,
то определитель полученной матрицы
равен произведению определителя исходной
матрицы
,
то определитель полученной матрицы
равен произведению определителя исходной
матрицы ![]() на
число
на
число ![]() в
степени, равной порядку матриц.
в
степени, равной порядку матриц.
Пример
Задание. Пусть
определитель матрицы ![]() третьего
порядка равен 3, вычислить определитель
матрицы
третьего
порядка равен 3, вычислить определитель
матрицы ![]() .
.
Решение. По
свойству ![]()
Ответ. ![]()
4. Если каждый элемент в какой-то строке определителя равен сумме двух слагаемых, то исходный определитель равен сумме двух определителей, в которых вместо этой строки стоят первые и вторые слагаемые соответственно, а остальные строки совпадают с исходным определителем.

5. Если две строки определителя поменять местами, то определитель поменяет знак.
Пример
![]()
6. Определитель с двумя равными строками равен нулю.
Пример
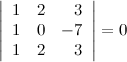
7. Определитель с двумя пропорциональными строками равен нулю.
Пример
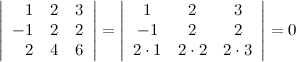
8. Определитель, содержащий нулевую строку, равен нулю.
Пример

9. Определитель не изменится, если к какой-то его строке прибавить другую строку, умноженную на некоторое число.
Пример
Пусть задан
определитель третьего порядка 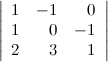 .
Прибавим ко второй строке определителя
третью его строку, при этом значение
определителя не измениться:
.
Прибавим ко второй строке определителя
третью его строку, при этом значение
определителя не измениться:
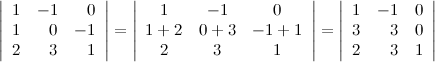
10. Определитель верхней (нижней) треугольной матрицы равен произведению его диагональных элементов.
Пример

11.
Определитель произведения
матриц равен
произведению определителей: ![]()
Метод Гаусса.
Метод Гаусса
является одним из наиболее эффективных
и универсальных методов решения линейных
систем. Процесс решения по методу Гаусса
состоит из двух этапов. На первом этапе
система
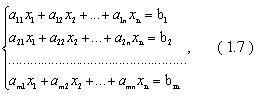
где aij - коэффициенты при неизвестных (первый индекс указывает номер уравнения, второй- номер неизвестной), bi - свободные члены. приводится к треугольному виду; на втором этапе идет последовательное определение неизвестных из полученной треугольной системы. Пусть в системе (1.7) а 11 не равно 0. Этого можно добиться несколькими способами, в числе которых перестановка уравнений местами, элементарные преобразования над строками. Все преобразования в дальнейшем будем проводить с расширенной матрицей. Нужно исключить все коэффициенты при х1, т.е. обратить все элементы первого столбца, начиная со второй строки в 0. Разделим первую строку на а 11 , т.е. преобразуем систему в равносильную так, чтобы а 11 =1. Для определенности, выберем неизвестное х1 так, чтобы коэффициент при нем не был равен 0.
![]()
Исключим теперь х1 из остальных уравнений системы. Будем умножать первую строку расширенной матрицы (1.9)(в нашем случае строка имеет вид- 1.10) последовательно на а21, а31,..., а n 1 и вычитать соответственно из 2-й, 3-й и т.д. строк и, наконец, из последней строки. Преобразованная расширенная матрица будет соответствовать системе уравнений с n неизвестными:
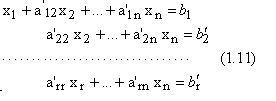
Применяя предложенным метод исключения теперь ко второй, третьей и т.д. строкам, получаем систему вида
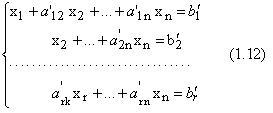
Возможны следующие случаи.
1. Одна из строк расширенной матрицы соответствует уравнению вида: 0+0+0+...+0= b'r . Причем b'r не равен 0. В этом случае система несовместна.
2. Последнее уравнение системы имеет вид: a' nn xn = b'n
В этом случае
получаем единственное решение.

