
Решение систем линейных уравнений в матричной форме.
Пусть для
матрицы А порядка n на n существует
обратная матрица ![]() .
Умножим обе части матричного
уравнения
.
Умножим обе части матричного
уравнения ![]() слева
на
слева
на ![]() (порядки
матриц A
⋅
X и В позволяют
произвести такую операцию, смотрите
статью операции
над матрицами, свойства операций).
Имеем
(порядки
матриц A
⋅
X и В позволяют
произвести такую операцию, смотрите
статью операции
над матрицами, свойства операций).
Имеем ![]() .
Так как для операции умножения матриц
подходящих порядков характерно свойство
ассоциативности, то последнее равенство
можно переписать как
.
Так как для операции умножения матриц
подходящих порядков характерно свойство
ассоциативности, то последнее равенство
можно переписать как ![]() ,
а по определению обратной матрицы
,
а по определению обратной матрицы ![]() (E–
единичная матрица порядка n на n),
поэтому
(E–
единичная матрица порядка n на n),
поэтому
 Таким
образом, решение
системы линейных алгебраических
уравнений по матричному методу
определяется равенством
Таким
образом, решение
системы линейных алгебраических
уравнений по матричному методу
определяется равенством ![]() .
Другими словами, решение СЛАУ находится
с помощью обратной матрицы
.
Другими словами, решение СЛАУ находится
с помощью обратной матрицы ![]() .
Мы
знаем, что квадратная
матрица А порядка n на n имеет
обратную матрицу
.
Мы
знаем, что квадратная
матрица А порядка n на n имеет
обратную матрицу ![]() только
тогда, когда ее определитель не равен
нулю. Следовательно, СИСТЕМУ n ЛИНЕЙНЫХ
АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ С nНЕИЗВЕСТНЫМИ
МОЖНО РЕШАТЬ МАТРИЧНЫМ МЕТОДОМ ТОЛЬКО
ТОГДА, КОГДА ОПРЕДЕЛИТЕЛЬ ОСНОВНОЙ
МАТРИЦЫ СИСТЕМЫ ОТЛИЧЕН ОТ НУЛЯ.
только
тогда, когда ее определитель не равен
нулю. Следовательно, СИСТЕМУ n ЛИНЕЙНЫХ
АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ С nНЕИЗВЕСТНЫМИ
МОЖНО РЕШАТЬ МАТРИЧНЫМ МЕТОДОМ ТОЛЬКО
ТОГДА, КОГДА ОПРЕДЕЛИТЕЛЬ ОСНОВНОЙ
МАТРИЦЫ СИСТЕМЫ ОТЛИЧЕН ОТ НУЛЯ.
С помощью обратной
матрицы найдите решение системы линейных
уравнений 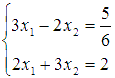 .
Решение.
В
матричной форме исходная система
запишется как
.
Решение.
В
матричной форме исходная система
запишется как ![]() ,
где
,
где 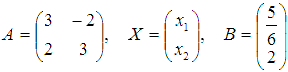 .
Вычислим определитель основной матрицы
и убедимся, что он отличен от нуля. В
противном случае мы не сможем решить
систему матричным методом. Имеем
.
Вычислим определитель основной матрицы
и убедимся, что он отличен от нуля. В
противном случае мы не сможем решить
систему матричным методом. Имеем  ,
следовательно, для матрицы А может
быть найдена обратная матрица
,
следовательно, для матрицы А может
быть найдена обратная матрица ![]() .
Таким образом, если мы отыщем обратную
матрицу, то искомое решение СЛАУ определим
как
.
Таким образом, если мы отыщем обратную
матрицу, то искомое решение СЛАУ определим
как ![]() .
Итак, задача свелась к построению
обратной матрицы
.
Итак, задача свелась к построению
обратной матрицы ![]() .
Найдем ее.
Мы знаем, что для
матрицы
.
Найдем ее.
Мы знаем, что для
матрицы 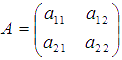 обратная
матрица может быть найдена как
обратная
матрица может быть найдена как 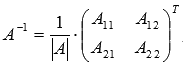 ,
где
,
где ![]() -
алгебраические дополнения элементов
-
алгебраические дополнения элементов ![]() .
В
нашем случае
.
В
нашем случае
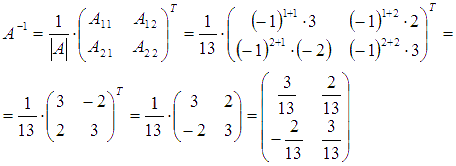 Тогда
Тогда
 Выполним
проверку полученного решения
Выполним
проверку полученного решения 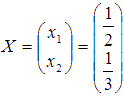 ,
подставив его в матричную форму исходной
системы уравнений
,
подставив его в матричную форму исходной
системы уравнений ![]() .
Это равенство должно обратиться в
тождество, в противном случае где-то
была допущена ошибка.
.
Это равенство должно обратиться в
тождество, в противном случае где-то
была допущена ошибка.
 Следовательно,
решение найдено верно.
Ответ:
Следовательно,
решение найдено верно.
Ответ: 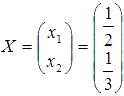 или
в другой записи
или
в другой записи ![]() .
.
Пример.
Решите
СЛАУ 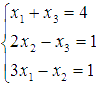 матричным
методом.
Решение.
Первое
уравнение системы не содержит неизвестной
переменной x2,
второе – x1,
третье – x3.
То есть, коэффициенты перед этими
неизвестными переменными равны нулю.
Перепишем систему уравнений как
матричным
методом.
Решение.
Первое
уравнение системы не содержит неизвестной
переменной x2,
второе – x1,
третье – x3.
То есть, коэффициенты перед этими
неизвестными переменными равны нулю.
Перепишем систему уравнений как  .
От такого вида проще перейти к матричной
форме записи СЛАУ
.
От такого вида проще перейти к матричной
форме записи СЛАУ 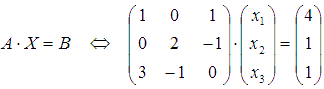 .
Убедимся в том, что эта система уравнений
может быть решена с помощью обратной
матрицы. Другими словами, покажем
что
.
Убедимся в том, что эта система уравнений
может быть решена с помощью обратной
матрицы. Другими словами, покажем
что ![]() :
:
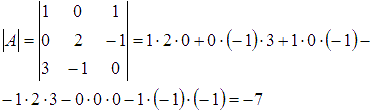 Построим
обратную матрицу
Построим
обратную матрицу ![]() с
помощью матрицы из алгебраических
дополнений:
с
помощью матрицы из алгебраических
дополнений:
 тогда,
тогда,
 Осталось
найти решение СЛАУ:
Осталось
найти решение СЛАУ:
 Рекомендуем
выполнить проверку.
Ответ:
Рекомендуем
выполнить проверку.
Ответ: 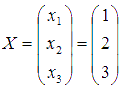 .
.
При переходе от
обычного вида системы линейных
алгебраических уравнений к ее матричной
форме следует быть внимательным с
порядком следования неизвестных
переменных в уравнениях системы. К
примеру, СЛАУ  НЕЛЬЗЯ
записать как
НЕЛЬЗЯ
записать как  .
Нужно сначала упорядочить все неизвестные
переменные во всех уравнениях системы,
а потом переходить к матричной
записи:
.
Нужно сначала упорядочить все неизвестные
переменные во всех уравнениях системы,
а потом переходить к матричной
записи:
 или
или
 Также
будьте внимательны с обозначением
неизвестных переменных, вместо x1,
x2,
…, xn могут
быть любые другие буквы. Например,
СЛАУ
Также
будьте внимательны с обозначением
неизвестных переменных, вместо x1,
x2,
…, xn могут
быть любые другие буквы. Например,
СЛАУ  в
матричной форме запишется как
в
матричной форме запишется как  .
Разберем
пример.
Пример.
Найдите
решение системы линейных алгебраических
уравнений
.
Разберем
пример.
Пример.
Найдите
решение системы линейных алгебраических
уравнений 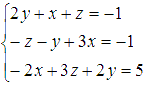 с
помощью обратной матрицы.
Решение.
Упорядочив
неизвестные переменные в уравнениях
системы, запишем ее в матичной форме
с
помощью обратной матрицы.
Решение.
Упорядочив
неизвестные переменные в уравнениях
системы, запишем ее в матичной форме  .
Вычислим определитель основной
матрицы:
.
Вычислим определитель основной
матрицы:
 Он
отличен от нуля, поэтому решение системы
уравнений может быть найдено с помощью
обратной матрицы как
Он
отличен от нуля, поэтому решение системы
уравнений может быть найдено с помощью
обратной матрицы как 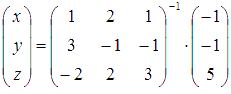 .
Найдем обратную матрицу по
формуле
.
Найдем обратную матрицу по
формуле 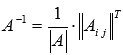 :
:
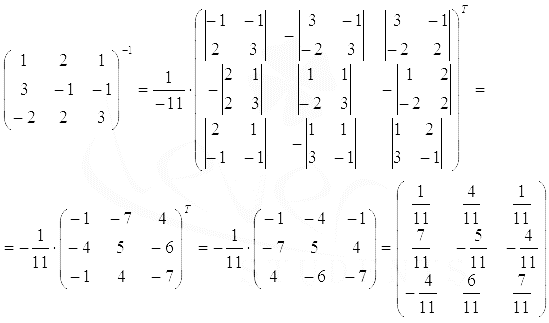 Получим
искомое решение:
Получим
искомое решение:
 Ответ: x
= 0, y = -2, z = 3.
Пример.
Найдите
решение системы линейных алгебраических
уравнений
Ответ: x
= 0, y = -2, z = 3.
Пример.
Найдите
решение системы линейных алгебраических
уравнений 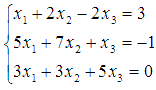 матричным
методом.
Решение.
Определитель
основной матрицы системы равен
нулю
матричным
методом.
Решение.
Определитель
основной матрицы системы равен
нулю
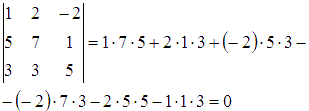 поэтому,
мы не можем применить матричный метод.
поэтому,
мы не можем применить матричный метод.
Пример.
Решите
СЛАУ 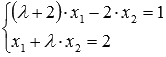 матричным
методом,
матричным
методом, ![]() -
некоторое действительное
число.
Решение.
Система
уравнений в матричной форме имеет вид
-
некоторое действительное
число.
Решение.
Система
уравнений в матричной форме имеет вид  .
Вычислим определитель основной матрицы
системы и убедимся в том, что он отличен
от нуля:
.
Вычислим определитель основной матрицы
системы и убедимся в том, что он отличен
от нуля:
 Квадратных
трехчлен
Квадратных
трехчлен ![]() не
обращается в ноль ни при каких
действительных значениях
не
обращается в ноль ни при каких
действительных значениях ![]() ,
так как его дискриминант отрицателен
,
так как его дискриминант отрицателен ![]() ,
поэтому определитель основной матрицы
системы не равен нулю ни при каких
действительных
,
поэтому определитель основной матрицы
системы не равен нулю ни при каких
действительных ![]() .
По матричному методу имеем
.
По матричному методу имеем 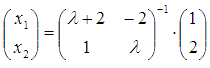 .
Построим обратную матрицу по
формуле
.
Построим обратную матрицу по
формуле 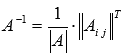 :
:
 Тогда
Тогда
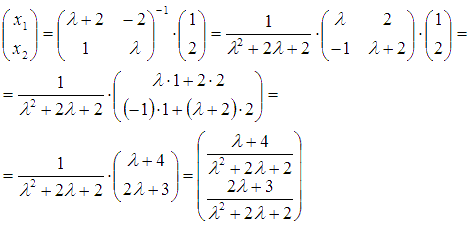 Ответ:
Ответ:  .
.
