Р е ш е н и е. Доля ценных бумаг портфеля, состоящего из двух типов этих бумаг, при их полной обратной корреляции находится по формулам

12.2. Портфель из двух типов ценных бумаг

Для каждого портфеля можно построить на графике ожидаемой доходности от стандартного отклонения точку, рассчитанную по формулам (12.1)—(12.3). Рассмотрим частный случай двух видов ценных бумаг. Пусть доля портфеля бумаг первого типа равна x , а бумаг второго типа равна 1 x . Введем следующие обозначения для математического ожидания доходностей бумаг первого и второго

типов, их дисперсий и ковариации a1; a2; 12; 22; 12 соответственно. Тогда (12.2) è (12.3) можно записать в виде:

является доля ценных бумаг x первого вида. Несколько графиков таких функций представлено на рис. 12.1. Некоторые из этих графиков имеют две ветви: верхнюю и нижнюю.

Найдем точку, в которой производная функции ap p стремится к бесконечности. Поскольку функция (12.12) задана параметрически,

Искомая точка находится из уравнения

x0 12 1 x0 2 22 1 2x0 12 0.

строку доходности и, нажав на кнопку «Диаграмма», откроем окно «Тип диаграммы». Выберем тип диаграммы «Точечная» и «Вид» такой, какой вас больше устраивает. Нажать на кнопку «Далее». В появившемся диалоговом окне раскрыть вкладку «Ряд». Поставить курсор в поле «Значения Х». Выделить строку рисков. Затем «Далее» «Далее» «Готово».

362 III. Фондовый рынок

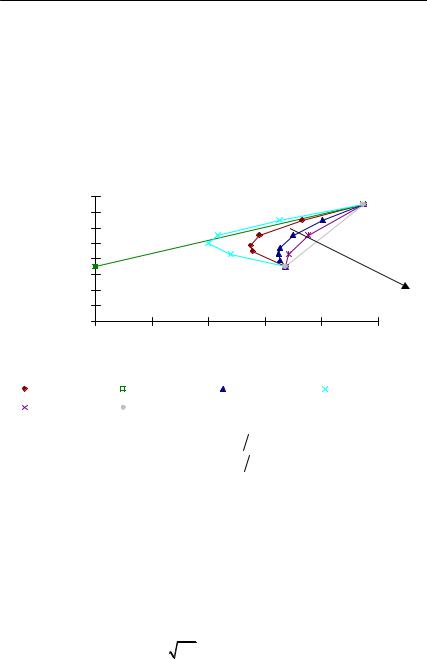
График, построенный по данным этой таблицы, представлен на рис. 12.1 ромбами. Эта кривая имеет вид «пули». p 0,548 — ìè-

нимальное из всех возможных средних квадратичных отклонений,

т.е. риск минимальный для структуры портфеля с долей бумаг первого типа x 0, 667 и с долей бумаг второго типа 1 x 0,333 .

При этом ожидаемая доходность равна ap 9, 664% . Для примера 2 можно записать:

ap xa1 1 x a2,

1 x .p 2

Доходность

изводная постоянная, то исследуемая функция является отрезком прямой линии. Для x 1 имеем ap a1 и p 0 . Åñëè

заданы точка, лежащая на прямой, и угловой коэффициент, то прямая определена. Ее уравнение имеет вид:

ap a1 a2 2a1 p .

Подставив сюда исходные данные примера, получим искомую функцию

ap 0, 07 0,15 0, 07 p 0, 07 0, 08433 p. 0,9

Отрезок прямой легко построить по двум точкам. Одна точка определена. Ее координаты (0; 0,07). Координаты второй точки находятся при x 0 . В этом случае ap a2, p 2 . Тогда ко-

ординаты второй точки (0,15; 0,949). На рис. 12.1 искомая функция представлена в виде левого отрезка прямой линии. Здесь же представлены графики других примеров. Стрелка показывает направление возрастания ковариации ценных бумаг первого и второго типов.

Для примера 6 из условия 12 1 следует 12 1 2 . Тогда можно записать

не зависит от стандартного отклонения портфеля, то искомая функция является отрезком прямой линии, соединяющим точ- ки, координаты которых находятся из условий:

Для условий примера первая точка имеет координаты (0,671; 0,07), а вторая – координаты (0,949; 0,15). На рис. 12.1 искомая функция изображена в виде правого отрезка прямой. 

Как следует из приведенных примеров, вид функции ap p

существенным образом зависит от ковариации двух доходностей ценных бумаг. При увеличении ковариации растет риск (стандартное отклонение) при той же доходности.

12.3. Оптимальный портфель

Ожидаемая доходность портфеля (12.2) и его дисперсия (12.3) зависят от структуры портфеля, т.е. от типов ценных бумаг и их доли от общего вложения. Можно построить оптимальный портфель, минимизирующий риск при определенных условиях. Можно, например, минимизировать дисперсию (12.3) при фиксированном уровне доходности (12.2) и при нормировании весовых коэффициентов (12.1). Такое решение минимизации риска впервые рассмотрено Марковицем [1—3]. Математическая формулировка задачи имеет вид: