Запишем систему в матричной форме:

Обозначим: 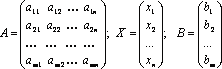, где

А – матрица коэффициентов при переменных, или матрица системы, Х – матрица-столбец переменных, В – матрица-столбец свободных членов.

Т.к. число столбцов матрицы равно числу строк матрицы, то их произведение:

Есть матрица-столбец. Элементами полученной матрицы являются левые части начальной системы. На основании определения равенства матриц начальную систему можно записать в виде: .

Теорема Крамера. Пусть - определитель матрицысистемы, а- определитель матрицы, получаемой из матрицызаменой-го столбца столбцом свободных членов. Тогда, если, то система имеет единственное решение, определяемое по формулам:

, - формула Крамера.

Пример. Решить систему уравнений по формулам Крамера

Р е ш е н и е. Определитель матрицы системы . Следовательно, система имеет единственное решение. Вычислим, полученные иззаменой соответственно первого, второго, третьего столбцов столбцом свободных членов:

По формулам Крамера:

.

 

№7Метод Гаусса  - метод последовательного исключения переменных.

Метод Гаусса заключается в том, что с помощью элементарных преобразований строк и перестановок столбцов система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида, из которой последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные.

Преобразования Гаусса удобно проводить не с самими уравнениями, а с расширенной матрицей их коэффициентов , получаемой приписыванием к матрицестолбца свободных членов:

.

Следует отметить, что методом Гаусса можно решить любую систему уравнений вида.

Пример. Методом Гаусса решить систему:

Выпишем расширенную матрицу системы.

Шаг 1. Поменяем местами первую и вторую строки, чтобы стал равным 1.

Шаг 2. Умножим элементы первой строки на (–2) и (–1) и прибавим их к элементам второй и третьей строк, чтобы под элементом в первом столбце образовались нули.

Шаг 3. Умножим элементы третьей строки на (–0,5).

Шаг 4. Поменяем местами вторую и третью строки.

Шаг 5. Поменяем местами второй и третий столбец. (Шаги 3, 4, 5 приведены с тем, чтобы ).

Шаг 6. Элементы второй строки умножим на 3 и прибавим их к элементам третьей строки, тогда под элементом появится нуль.

(называется расширенная матрица системы) .

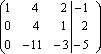
Расширенная матрица приведена к треугольному виду. Соответствующая ей система имеет вид:

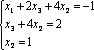
Из последнего уравнения  ; из второго; из первого.

Таким образом, ,,.

№8Система уравнений

Система m линейных уравнений с n переменными имеет вид:

или

(1)

где

произвольные числа, называемые соответственно коэффициентами при переменных и

- свободными членами уравнений.

Решением системы (1) называется такая совокупность n чисел

,

при подстановке которых каждое уравнение системы обращается в верное равенство.

Теоре́ма Кро́некера — Капе́лли — критерий совместности системы линейных алгебраических уравнений:

Система линейных алгебраических уравненийсовместнатогда и только тогда, когдарангеё основной матрицы равен рангу её расширенной матрицы, причём система имеет единственное решение, если ранг равен числу неизвестных, и бесконечное множество решений, если ранг меньше числа неизвестных.

1) Если решение существует, то столбец свободных членов есть линейная комбинация столбцов матрицы А, а значит добавление этого столбца в матрицу, т.е. переход АА^* не изменяют ранга.

            2) Если RgA = RgA^*, то это означает, что они имеют один и тот же базисный минор. Столбец свободных членов – линейная комбинация столбцов базисного минора, те верна запись, приведенная выше.

 Пример. Определить совместность системы линейных уравнений:

A =

 

~ .

                  

RgA = 2.

A* =

RgA* = 3.

            Система несовместна.

  Пример. Определить совместность системы линейных уравнений.

                       А = ;= 2 + 12 = 14 0;   

RgA = 2;

  A* =

 

RgA* = 2.

            Система совместна. Решения: x₁ = 1;  x₂ =1/2

№10 Однородной системой линейных уравнений называется система вида:

Нулевое решение системы (1) называется тривиальным решением.

однородные системы всегда совместны, т.к. всегда существует тривиальное решение.

Если существует любое ненулевое решение системы, то оно называется нетривиальным.

Решения однородной системы обладают свойством линейности: Теорема (о линейном решении однородных систем).

Пусть — решения однородной системы (1), — произвольные константы. Тогда также является решением рассматриваемой системы.

Сформулируем теорему, которая позволит дать основное определение:

Теорема (о структуре общего решения).

Пусть , тогда:

если , где — число переменных системы, то существует только тривиальное решение;

если , то существует линейно независимых решений рассматриваемой системы: , причём её общее решение имеет вид: , где — некоторые константы.

Пусть дана однородная система (1), тогда набор векторов размера называется фундаментальной системой решений (ФСР) (1), если:

— решения системы (1);

линейно независимы;

. Теорема (о ФСР).

Пусть ранг основной матрицы , где — число переменных системы (1), тогда:

ФСР (1) существует: ;

она состоит из векторов;

общее решение системы имеет вид .

Замечание:

Если , то ФСР не существует.

[править]

Пример

Решим систему

Перепишем её в матричном виде:

Путём элементарных преобразований над строками приведём её основную матрицу к ступенчатому виду:

Таким образом ранг системы (ранг её основной матрицы) равен двум. Это значит, что существует линейно независимых решения системы.

Перепишем полученную систему в виде уравнений:

Возьмём и в качестве главных переменных. Тогда:

Подставим по очереди единицы в качестве одной из свободных переменных: и .

Тогда общее решение рассматриваемой системы может быть записано так:

,а вектора составляют фундаментальную систему решений.

Однородная система уравнений

Предложение 15.2 Однородная система уравнений

(15.7)

всегда является совместной.

Доказательство. Для этой системы набор чисел , , , является решением.

В этом разделе мы будем использовать матричную запись системы: . Предложение 15.3 Сумма решений однородной системы линейных уравнений является решением этой системы. Решение, умноженное на число, тоже является решением.

Доказательство. Пусть и служат решениями системы . Тогда и . Пусть . Тогда

Так как , то -- решение.

Пусть -- произвольное число, . Тогда

Так как , то -- решение.

Следствие 15.1 Если однородная система линейных уравнений имеет ненулевое решение, то она имеет бесконечно много различных решений.

Действительно, умножая ненулевое решение на различные числа, будем получать различные решения.

Определение 15.5 Будем говорить, что решения системы образуют фундаментальную систему решений, если столбцы образуют линейно независимую систему и любое решение системы является линейной комбинацией этих столбцов.

Определение 15.6 Пусть -- фундаментальная система решений однородной системы . Тогда выражение

где -- произвольные числа, будем называть общим решением системы .

Из определения фундаментальной системы решений следует, что любое решение однородной системы может быть получено из общего решения при некоторых значениях . И наоборот, при любых фиксированных числовых значениях из общего решения получим решение однородной системы.

Как находить фундаментальную систему решений мы увидим позже, в разделе "Алгоритм нахождения решений произвольной системы линейных уравнений (метод Гаусса)".

Теорема 15.3 Пусть -- фундаментальная система решений однородной системы . Тогда , где -- число неизвестных в системе.

Доказательство читатель может найти, например, в [1].

№11. Умножение вектора на число

Произведением ненулевого вектора а на число х =/= 0 называется вектор, длина которого равна | x | • | а |, а направление совпадает с направлением а, если х > 0, и противоположно ему, если х < 0.

Произведением нулевого вектора на любое число х и произведением любого вектора на число нуль называется нулевой вектор.

Произведение вектора а на число х обозначается х • а (числовой множитель пишется слева).

Согласно определению | x • а | = | x | • | а | для любого вектора а и любого числа х.

На рис. 18 изображены произведения вектора а на число х = 2 (вектор CD>) и на число х = —2 (вектор EF>).

Умножение вектора на число обладает следующими свойствами:

1. Свойство ассоциативности (сочетательности):

х • (у • а) = (х • у) • а.

2. Свойство дистрибутивности (распределительности) относительно векторного множителя:х • а + y • а = (х + у) • а.

3. Свойство дистрибутивности (распределительности) относительно числового множителя:

х • а + х • b = х • (a + b).

Если a = 0 или ху = 0, то равенство х(уа) = = (ху)а очевидно, так как слева и справа стоят нулевые векторы.Пусть а =/= 0, ху =/= 0 и а = OA>. Тогда векторы х (у • OA>) и (ху) OA> лежат на прямой OA>, имеют длину |x| • |y| • |OA>| и направлены в одну сторону: в сторону вектора а = OA>, если ху > 0, и в противоположную сторону, если ху < 0. Таким образом, свойство 1 доказано.Свойства 2 и 3 доказывать не будем. Заметим лишь, что свойства 1 и 2 являются свойствами векторов на прямой. Они уже доказывались в курсе геометрии восьмилетней школы. Свойство 3 является свойством векторов на плоскости; оно тоже было доказано.

Задача. В параллелограмме ABCD точка М есть точка пересечения диагоналей. Найти множитель k в каждом из следующих случаев:

1) M C> = k • CA>; 2) BD> = k • BM>; 3) AC> = k • CM>;

4) BB> = k • BD>; 5) AA> = k • CC>.

В соответствии с определением умножения вектора на число имеем (рис. 19)

1) M C> CA> , | CA| = 2•| MC |, откуда k = — 1/2;

2) BM> BD>, | BD | = 2 • | ВМ |, откуда k = 2;

3) CM> AC>, | CM | = 1/2• |AС |, откуда k = -2;

4) BB> = 0, BD> =/= 0, откуда k = 0;

5) AA> = 0, CC> = 0, откуда k — любое число.

Векторы на плоскости и в пространстве