№1 Матрицей размера называется прямоугольная таблица, содержащаяm строк и n столбцов.

Матрицы широко применяются для описания экономических объектов и процессов. Элементами матрицы могут быть числа, буквы (символы) и другие объекты.

Матрицы обозначают прописными (заглавными) буквами A, B, C, …, элементы матрицы – строчными буквами с двойной индексацией aij, где i - номер строки, j - номер столбца:

1) Матрица-строка: ;

2) Матрица-столбец: 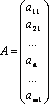;  3) Нулевая матрица: ;

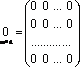4) Квадратная матрица – если (напримерn = 2): ;

5) Диагональная матрица (напр. 3-го порядка, где любые числа):;

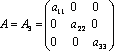6) Единичная матрица (например, 3-го порядка)

Пусть -- матрица размеров. Тогдатранспонированной матрицей называется такая матрицаразмеров, что,,.

Транспонированная матрица обозначаетсяили. Операция транспонирования заключается в том, что строки и столбцы в исходной матрице меняются ролями. В транспонированной матрице первым столбцом служит первая строка исходной матрицы, вторым столбцом -- вторая строка исходной матрицы и т.д. Например,

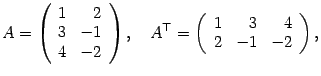
Две матрицы иодинакового размераm на n называются равными, если ,i = 1,2,…,m, j=1,2,…,n.

Если матрицы A и B равны, то будем писать A=B.

Операция сложения матриц обладает следующими свойствами: для любых матриц и нулевой матрицы

1) A+B=B+A; (перестановочность или коммутативность операции сложения

2) (A+B)+C = A+(B+C); (ассоциативность или сочетательное свойство)

3) A+O = O+A =A;

4) A+(-A)=(-A)+A=O.

Перечисленные выше свойства непосредственно вытекают из определения и доказываются по единой схеме.

Произведением матрицы на числоназывается матрица, элементы которой определены равенством

Произведение матрицы A на число будем обозначать.

Теорема 2.2 Операция умножения матрицы на число обладает следующими свойствами:

1) ;

2) ;

3) (Распределительное свойство относительно сложения матриц);

4) (Распределительное свойство относительно сложения чисел);

5) -A=(-1)A.

Все перечисленные свойства непосредственно вытекают из определения.

Операции сложения матриц и умножения матрицы на число позволяют для произвольных матриц одинакового размераи произвольных чиселоднозначно определить матрицу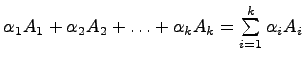, называемуюлинейной комбинацией матриц с коэффициентами.

Умножение матриц. Произведением матриц иназывается матрица, элементы которой определены равенством

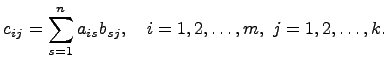
Произведение матриц A и B будем обозначать C=AB.

Из определения следует, что произведение AB определено лишь в том случае, когда число столбцов матрицы A совпадает с числом строк матрицы B. Это означает, что оба произведения AB и BA определены тогда и только тогда, когда матрицы A и B имеют размеры исоответственно. Следовательно равенствоAB=BA возможно лишь для квадратных матриц одинакового порядка. Однако и в этом случае произведение матриц, вообще говоря, зависит от порядка сомножителей.

Матрицы A и B называются перестановочными или коммутирующими, если AB=BA.

Теорема 2.3 Операция умножения матриц обладает следующими свойствами:

1) (AB)C=A(BC); (Свойство ассоциативности)

2) , для любого действительного числа

3) A(B+C)=AB+AC, (A+B)C=AC+BC (Свойство дистрибутивности), для любых матриц A, B, C, для которых левые части равенств имеют смысл.

Справедливость свойств 2) и 3) доказываются непосредственно.

В качестве иллюстрации приведём доказательство первого равенства свойства 3). Пусть ,,. МатрицыA(B+C) и AB+AC имеют одинаковый размер - . Пусть- элемент матрицыA(B+C) в позиции (i,j), - элемент матрицыAB+AC в позиции (i,j), тогда

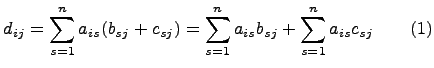
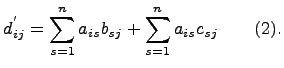
Из равенств (1) и (2) следует, что , что доказывает первое равенство свойства 3).

Подробное доказательство свойства 1) можно найти в учебнике В. А. Ильин, Г. Д. Ким "Линейная алгебра и аналитическая геометрия".

Заметим, что для любой матрицы и единичных матрицыисправедливо:

Транспонирование матриц. Пусть . Матрицаназываетсятранспонированной к матрице A, если

Транспонированная матрица также обозначается символами и.

Заметим, что при транспонировании матрицы её строки становятся столбцами матрицы , с теми же номерами, а столбцы - строками.

№2 Определитель – это некоторое число поставленное в соответствие квадратной матрице Определитель матрицы размера n × n равен ориентированному n-мерному объёму параллелепипеда, натянутого на её векторы-строки (или столбцы).

1. Определитель , имеющий строку, представленной суммой двух строк, равносилен сумме определителей

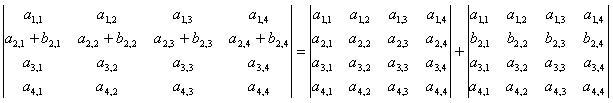
2. Определитель , имеющий нулевую строку, равен нулю

3. Определитель , имеющий две пропорцинальных строки , равен нулю

4. Определитель единичной матрицы равен единице

5. Опредилетель транспонированной матрицы равен определителю не транспонированной матрицы

6. Определитель не изменится, если из строки вынести множитель

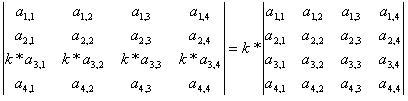
7. Определитель не изменится, если одну из его строк домножить на число и добавить к другой cтроке 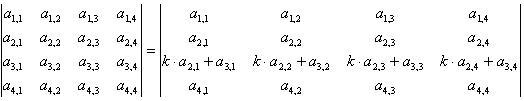(в силу свойства 3)

8. При перестановке двух строк определителя, определитель меняет знак

9. Все свойства сформулированые для строк, верны и для столбцов(в силу свойства 5 )

. Теорема лапласа

Определитель квадратной матрицы равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения:

(*)

(разложение по элементам i-й строки);

(**)

(разложение по элементам j-го столбца).

Убедимся в справедливости теоремы Лапласа на примере определителя матрицы третьего порядка. Разложим его вначале по элементам первой строки

Что совпадает с определением определителя матрицы третьего порядка.

Пример 1. Вычислить определитель третьего порядка

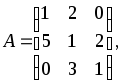
используя его разложение по элементам первой строки.

Решение. Находим алгебраические дополнения элементов первой строки:

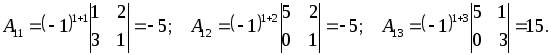
Теперь по теореме Лапласа найдем определитель, используя формулу (*)

Пример 2. Вычислить определитель предыдущего примера, используя его разложение по элементам второго столбца.

Решение. Находим алгебраические дополнения элементов второго столбца:

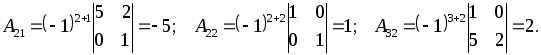
Теперь по формуле (**) найдем определитель матрицы

Значения первого и второго примеров совпали, что говорит о том, что можно выбирать разложение по любой строке или любому столбцу.

Пример 3. Вычислить определитель четвертого порядка треугольной матрицы:

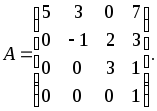
Решение: Выполним разложение по первому столбцу:

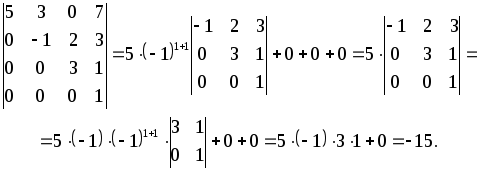
Значение теоремы Лапласа состоит в том, что она позволяет свести вычисление определителей n-го порядка к вычислению определителя меньшего порядка, то есть (n-1)-го порядка.

№3Обратная матрица

Для каждого числа существует обратное числотакое, что произведение. Для квадратных матриц тоже вводится аналогичное понятие.

Определение. Матрица называется обратной по отношению к квадратной матрице, если при умножении этой матрицы на данную как справа, так и слева получается единичная матрица:

.

Только квадратная матрица может иметь обратную, однако не каждая квадратная матрица имеет обратную.

Определение. Матрица являетсяневырожденной (неособенной), если , в противном случае приматрицаназываетсявырожденной (особенной).

Теорема (необходимое и достаточное условие существования обратной матрицы). Обратная матрицасуществует (и единственна) тогда и только тогда, когда исходная матрица является невырожденной (неособенной) и вычисляется по формуле

,

где - присоединенная матрица, состоящая из алгебраических дополнений элементов транспонированной матрицы, т.е..

Необходимость. Пусть матрица имеет обратную, т.е.. По свойству 10 определителей имеем:, т.е.и.

Достаточность. Пусть . Рассмотрим квадратную матрицу n-го порядка, называемую присоединенной, элементы которой являются алгебраическими дополнениями элементов матрицы, транспонированной к. Тогда элементы произведения матрицопределяются по правилу умножения матриц. Поэтому матрица В является диагональной, элементы ее главной диагонали равны определителю исходной матрицы. А произведениенаравно той же матрице В:.

Единственность обратной матрицы. Предположим, что существуют еще матрицы итакие, чтои, где матрицаполучена по формулеи выполняются равенстваи. Тогда, умножая наслева первое из них, получаем:, откуда, т.е.. Аналогично, умножая второе равенство насправа, получаем. Единственность доказана.