МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
ВСЕРОССИЙСКИЙ ЗАОЧНЫЙ ФИНАНСОВО-ЭКОНОМИЧЕСКИЙ ИНСТИТУТ (ВЗФЭИ)
Филиал ВЗФЭИ в г. Краснодаре
Кафедра Экономико-математических методов и моделей
Контрольная работа
по дисциплине «Экономико-математические методы
и прикладные модели»
на тему «Вариант № 1»
|
Выполнил(а): |
|
|
Факультет: |
непрерывного образования |
|
Уровень: |
Повышенный |
|
Направление: |
Бакалавр экономики |
|
№ зачетной книжки: |
|
|
Руководитель: |
|
Краснодар 2011
Содержание.
Задание 1.Теоретическая часть…………………….……………………….3
Задание 2. Практическая часть.
Задача №1………………………………………………………………………..4
Задача № 2………………………………………………………………………..7
Задача № 3………………………………………………………………………17
Список использованной литературы………………………………….………22
Задание 1.
Теоретическая часть. Особые случаи решения злп графическим методом.
При решении некоторых ЗЛП графическим методом может встретиться случай, когда линия уровня параллельна одной из сторон выпуклого многоугольника допустимых решений, причем это сторона расположена в направлении смещения линии уровня при стремлении целевой функции к своему оптимуму. В этом случае оптимальное значение целевой функции достигается не в одной, а в двух угловых точках (вершинах) многоугольника решений и, следовательно, во всех точках отрезка, соединяющего эти вершины, т.е. задача будет иметь бесчисленное множество решений (пример 1.1.).
Если
область допустимых решений является
незамкнутым выпуклым многоугольником
в направлении оптимизации целевой
функции, то целевая
функция будет неограниченной и
ЗЛП
не будет иметь решений;
в этом случае можно записать, что,
например, max
f(
)
= +∞ (пример 1.2.).
Очевидно также, что ЗЛП не будет иметь решений в случае, когда область допустимых решений есть пустое множество, т.е. система ограничений ЗЛП содержит противоречивые неравенства, и на координатной плоскости нет ни одной точки, удовлетворяющей этим ограничениям (пример 1.3.).
Пример
1.1. Найти
максимум и минимум f(
):
f(
)=
3x1
+ 3x2
при ограничениях
x1 + x2 ≤ 8, (1)
2x1 – x2 ≥ 1, (2)
x1 – 2x2 ≤ 2, (3)
x1,2 ≥ 0.
Решение. При решении данного примера на максимум возникает ситуация, когда линия уровня 3x1 + 3x2 = a параллельна первому ограничению: x1 + x2 ≤ 8. Целевая функция достигает максимального значения в двух точках: A (3; 5) и В (6; 2) – и принимает на отрезке АВ одно и тоже значение, равное 24:
f(
)=
3x1
+ 3x2
=
3 * 3 + 3 * 5 = 3 * 6 + 3 * 2 = 24.
При решении данного примера на минимум целевой функции линию уровня 3x1 + 3x2 = a следует двигать в направлении, обратном направлению вектора-градиента. Целевая функция достигает минимального значения в точке D (0,5; 0):
f(
)=
3x1
+ 3x2
=
3 * 0,5 + 3 * 0 = 1,5.
Ответ:
max
f(
)
= 24; min
f(
)
= 1,5.
Задание 2. Практическая часть.
Задача №1
Инвестор располагающий суммой в 300 тыс. ден. ед., может вложить свой капитал в акции автомобильного концерна А и строительство предприятия В. Чтобы уменьшить риск, акций А должно быть приобретено на сумму по крайней мере в два раза большую, чем акций В, причём последних можно купить не более, чем на 100 тыс. ден. ед.
Дивиденды по акциям составляют 8% в год, а по акциям В – 10%. Какую максимальную прибыль можно получить в первый год?
Построить экономико-математическую модель задачи, дать необходимые комментарии к её элементам и получить решение графическим методом. Что произойдёт, если решить задачу на минимум, и почему?
Решение.
Сформулируем экономико-математическую модель задачи. Обозначим через х1 объём денежных средств вложенных в акции автомобильного концерна А, х2 – инвестиции в акции строительного предприятия В. Прибыль по акции автомобильного концерна А составляет 0, 08 х1, а по акциям строительного предприятия В – 0,1х2, т.е. необходимо максимизировать целевую функцию:
f
(
)
= 0,08х1
+ 0,1х2
max,
при
ограничениях х1
+ х2
300 (1)
х1
- 2х2
0 (2)
х1
- х2
100 (3)
х1
0х2
0 (4)
Условие (1) отражает общую располагающую сумму вложений в акции, (2) и (3) – ограничения по сумме возможного приобретения акций, (4) условия неотрицательных значений.
Для решения задачи графическим методом найдём область допустимых значений задачи.
Прямые ограничения означают, что область решения будет лежать в первой четверти декартовых координат.
Определим
множество решений первого неравенства
х1
+ х2
300.
Решением уравнения служат точки прямой х1 + х2 – 300 = 0. Построим прямую по двум точкам (0;300) и (300;0), которые получаем, подставляя в уравнение вместо одной из переменных 0 (на рис.1 обозначаем её цифрой Ι). Найдём область решения неравенства, для этого подставим координаты (0:0), получаем
0 < 300,т.е. оно выполняется. Следовательно. Областью решения неравенства служит нижняя полуплоскость.
Аналогично строим области решения двух других неравенств
х1
- 2х2
0
х1 - 2х2 = 0; х1 = 0 х2 = 0 Получаем точку с координатами (0,0). Это означает, что данная точка входит в ОДР задачи.
х1
- х2
100;х1
=
0 х2
=
-100
х1 =100 х2 = 0 . (на рис. прямая ΙΙ)
х1
- х2
100 при
х1 =
х2
=
0, 0<100 выполняется, берётся верхняя
полуплоскость.
Заштрихуем общую область для всех неравенств, обозначим вершины четырёхугольника латинскими буквами ОАВС – ОДР задачи.
Для
определения направления движения к
оптимуму построим вектор градиент
,
координаты которого являются частными
производными функции
f
(
),
т.е.
=(с1;с2)=
(0,08;0,1). Чтобы построить этот вектор,
нужно соединить точку (0,08;0,1) с началом
координат. Для удобства строим вектор
пропорциональный вектору
,
1000
=(80;100).
Построим линию уровня целевой функции перпендикулярную вектору-градиенту: приравняем целевую функцию постоянной величине а
0,08х1 + 0,1х2=а
Вычислим координаты двух точек, если а = 0, то
0,08х1 + 0,1х2=0; х1=100;х2=-80
х1=-100;х2=80
Линия уровня проходит через точку (100;-80) и (-100;80).
Для
нахождения f
(
)
= 0,08х1
+ 0,1х2 необходимо линию уровня смещать
параллельно себе в направлении
вектора-градиента
.
Максимум целевой
функции достигает в точке В полученной путём пересечения двух прямых.
Найдём координаты точки В, для этого достаточно решить два уравнения:
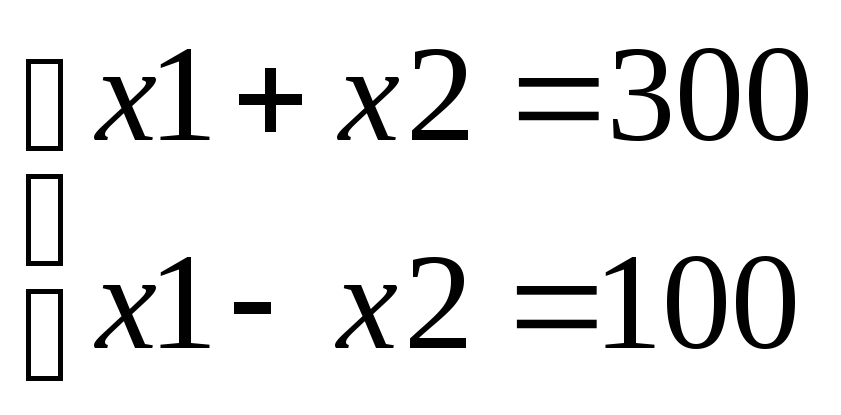
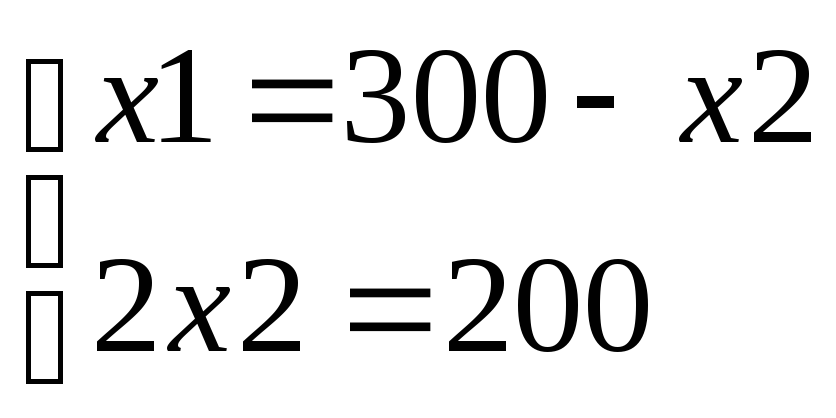
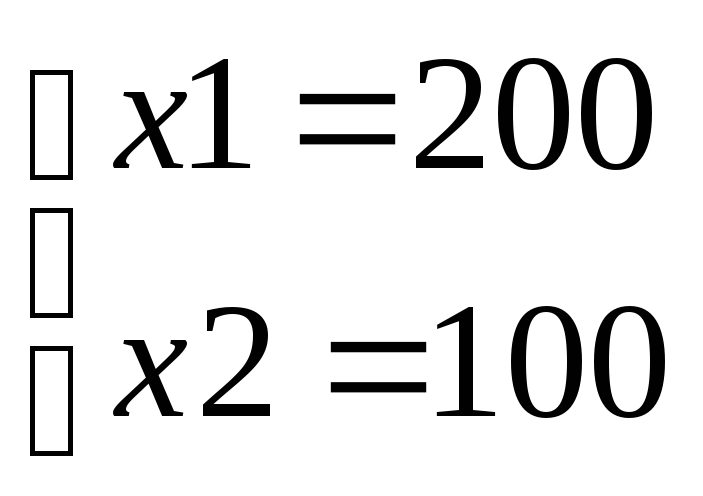
Отсюда
решение
f
(
)
=26 и достигается прих1=200;
х2=100.
Если
поставить задачу минимизировать функцию
f
(
)
= 0,08х1
+ 0,1х2 при тех же ограничениях, линию
уровня необходимо смещать параллельно
самой себе в направлении, противоположном
вектору-градиенту. Как это видно на
рис.1, минимум целевой функции достигается
в точке О(0;0),
следовательно, можно записать min
f
(
)=0
и достигается при х1=0; х2=0.
Задача № 2.
В течение девяти последовательных недель фиксировался спрос Y(t) (млн.руб.) на кредитные ресурсы финансовой компании. Временной ряд Y(t) приведён в таблице:
|
Номер наблюдения (t=1.2.3….9) | ||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
10 |
14 |
21 |
24 |
33 |
41 |
44 |
47 |
49 |
Требуется:
1) Проверить наличие аномальных наблюдений.
2)
Построить линейную модель
,
параметры которой оценить МНК (Y(t)
– расчётные, смоделированные значения
временного ряда).
3) Оценить адекватность построенных моделей, используя свойства независимости остаточной компоненты, случайности и соответствия нормальному закону распределения (при использовании R/S критерия взять табулированные границы 2,7 – 3,7).
4) Оценить точность моделей на основе использования средней относительной ошибки аппроксимации.
5) По двум построенным моделям осуществить прогноз спроса на следующие две недели ( доверительный интервал прогноза рассчитать по доверительной вероятности р=70%).
6) Фактические значения показателя, результаты моделирования и прогнозирования представить графически.
Решение:
Под аномальным уровнем понимается отдельное значение уровня временного ряда, которое не отвечает потенциальным возможностям исследуемой экономической системы и которое, оставаясь в качестве уровня ряда, оказывает существенное влияние на значения основных характеристик временного ряда, в том числе и на соответствующую трендовую модель.
Для выявления аномальных наблюдений воспользуемся методом Ирвина:
где
среднеквадратическое отклонение
рассчитываем с использованием формул:
;
.
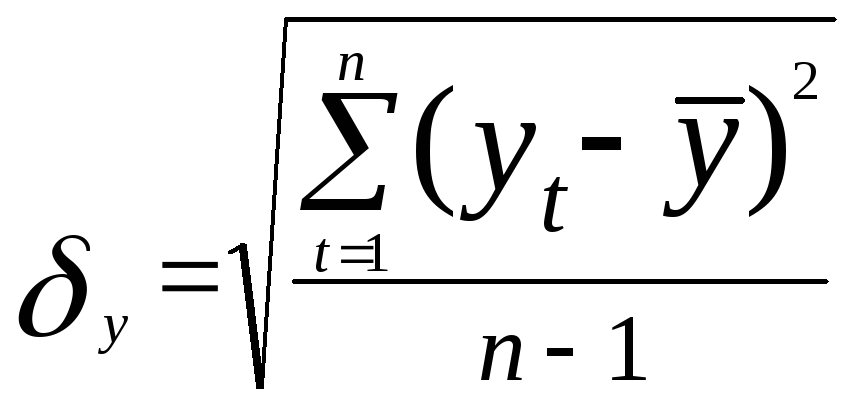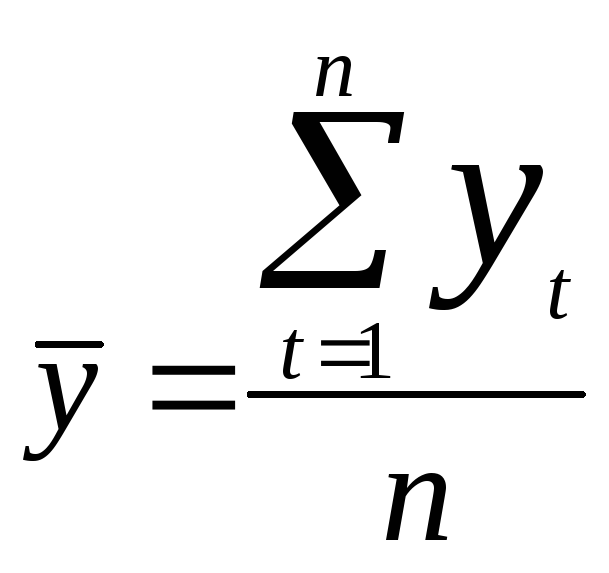Расчётные
значения
и
т.д. сравниваются с табличными значениями
критерия Ирвина
,
и если оказывается больше табличных,
то соответствующее значение уt
уровня ряда считается аномальным. При
п=9 для уровня значимость
значение
критерия Ирвина равно 1,5. Все расчётные
значения представим в таблице:
|
t |
|
|
( |
|
|
|
1 |
10 |
-21,4 |
438,4 |
- |
- |
|
2 |
14 |
-17,4 |
286,9 |
4 |
0,27 |
|
3 |
21 |
-10,4 |
98,6 |
7 |
0,48 |
|
4 |
24 |
-7,4 |
48,0 |
3 |
0,20 |
|
5 |
33 |
1,6 |
4,0 |
9 |
0,61 |
|
6 |
41 |
9,6 |
100,9 |
8 |
0,54 |
|
7 |
44 |
12,6 |
170,2 |
3 |
0,20 |
|
8 |
47 |
15,6 |
257,5 |
3 |
0,20 |
|
9 |
49 |
17,6 |
325,8 |
4 |
0,27 |
|
∑ |
283 |
- |
1730,2 |
- |
- |
)2
Отсюда
<
1,5, что означает данный временной ряд,
не содержит аномальных наблюдений.
2)
Построим линейную модель
.
Промежуточные расчёты параметров
линейной модели приведём в табл.
|
t |
|
|
|
|
|
|
|
|
1 |
10 |
-4 |
16 |
-21,4 |
85,8 |
10,24 |
-0,24 |
|
2 |
14 |
-3 |
9 |
-17,4 |
52,3 |
15,54 |
-1,54 |
|
3 |
21 |
-2 |
4 |
-10,4 |
20,9 |
20,84 |
0,16 |
|
4 |
24 |
-1 |
1 |
-7,4 |
7,4 |
26,14 |
-2,14 |
|
5 |
33 |
0 |
0 |
1,6 |
0,0 |
31,44 |
1,56 |
|
6 |
41 |
1 |
1 |
9,6 |
9,6 |
36,74 |
4,26 |
|
7 |
44 |
2 |
4 |
12,6 |
25,1 |
42,04 |
1,96 |
|
8 |
47 |
3 |
9 |
15,6 |
46,7 |
47,34 |
-0,34 |
|
9 |
49 |
4 |
16 |
17,6 |
70,2 |
52,64 |
-3,64 |
|
∑ |
283 |
- |
60 |
- |
318,0 |
283,0 |
- |
-
(
-
)
.
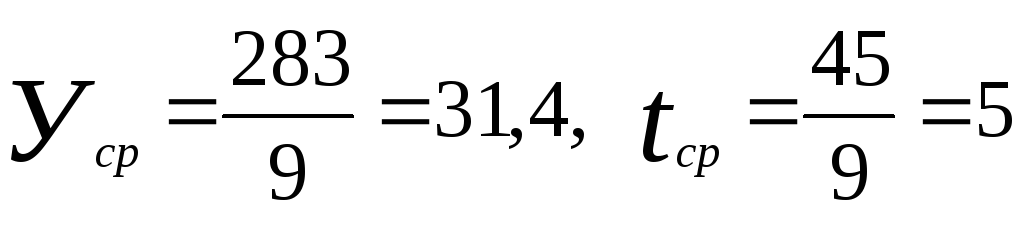
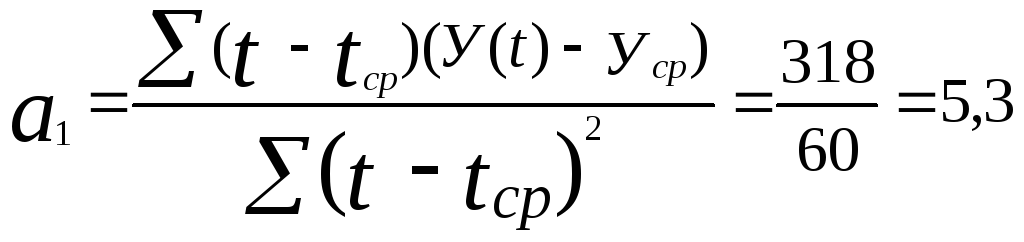
Таким
образом, линейная модель имеет вид:
=4,94+5,3t.
Последовательно подставляя в модель
вместо фактора t его значения от 1 до n,
получаем расчётные значения уровней
:
=4,94+5,3·1=10,24
=4,94+5,3·2=15,54
Отклонения
расчётных значений от фактических
наблюдений находим по формуле:
=
-
(t=1,2,…..9).
3.Оценим адекватность построенных моделей.
р
>
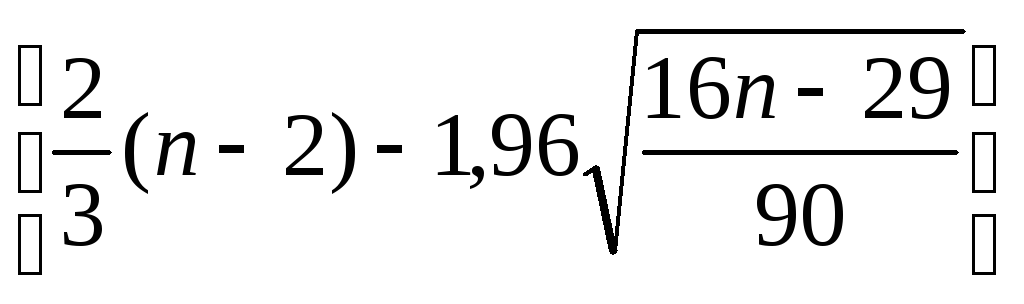
р > 2 , так как правая часть неравенства равна 2, т.е. неравенство выполняется. Можно сделать вывод, что свойство случайности ряда остатков подтверждается.
Для проверки независимости уровней ряда остатков вычисляем значение критерия Дарбина-Уотса по формуле:
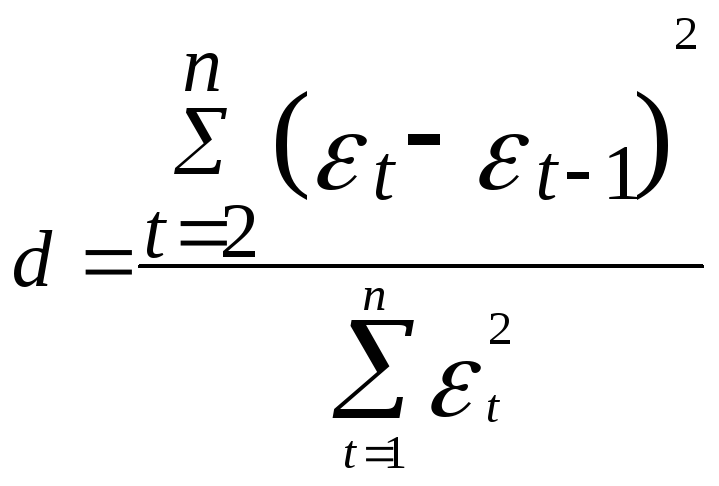
Расчёт представлен в таблице ниже. Критерий d=1,16, так как и попал в интервал (0,98-1,36), то по данному критерию нельзя сделать вывод о выполнении свойства независимости. Необходимо вычислить коэффициент автокорреляции первого порядка:
=
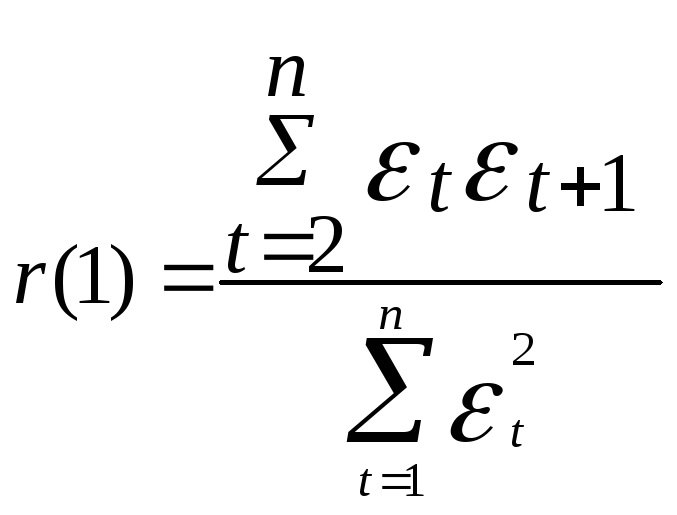0,26
фактическое
значение больше табличного. Это означает,
что в ряду динамики имеется автокорреляция,
следовательно, модель по этому критерию
неадекватна. Соответствие ряда
остатков нормальному закону распределения
определяем при помощи R/S
критерия:
.
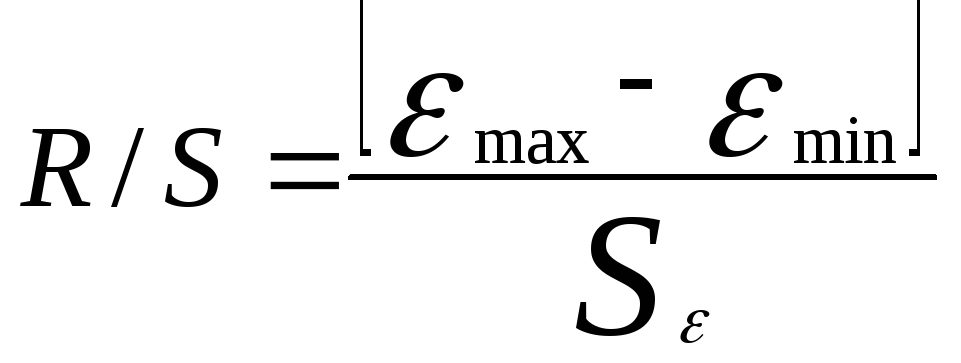Размах
вариации:
,
а среднее квадратическое отклонение
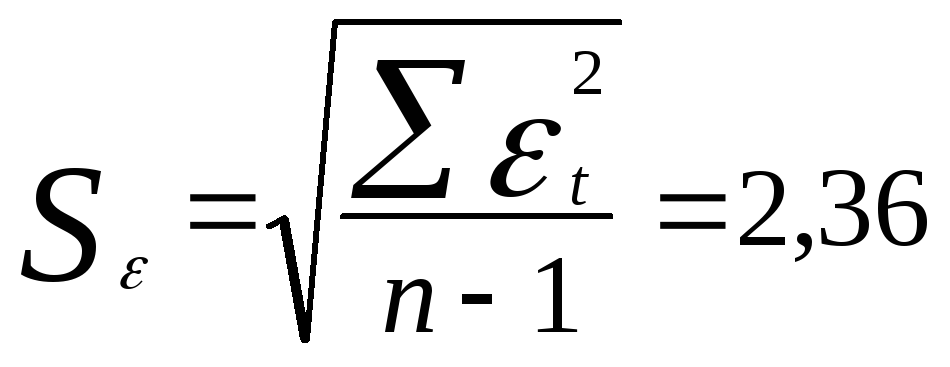
Следовательно, R/S=3,34. Это значение попадает в интервал между нижней и верхней границами табличных значений данного критерия (2,7-3,7). Следовательно, свойство нормальности распределения выполняется.
3) Оценим адекватность построенных моделей.
р
>
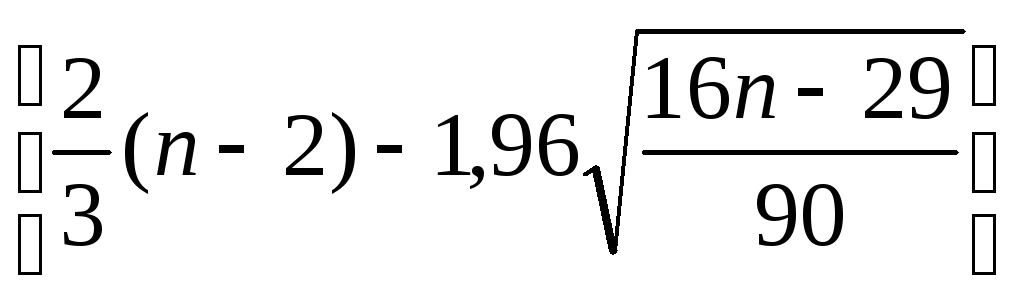
р > 2 , так как правая часть неравенства равна 2, т.е. неравенство выполняется. Можно сделать вывод, что свойство случайности ряда остатков подтверждается.
Для проверки независимости уровней ряда остатков вычисляем значение критерия Дарбина-Уотса по формуле:
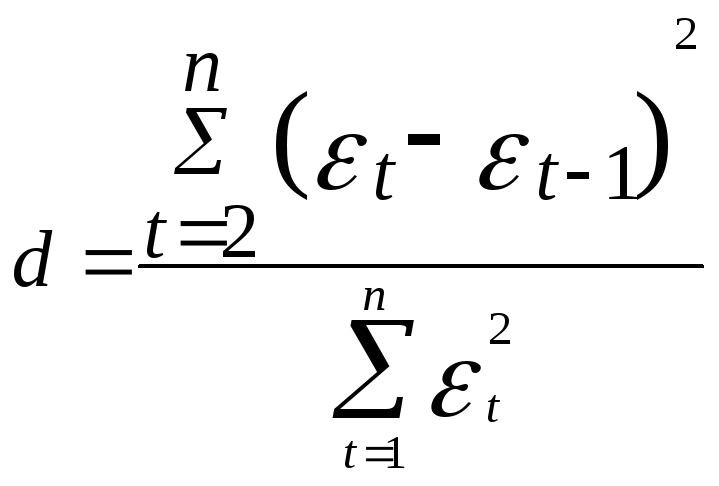
Расчёт представлен в таблице ниже. Критерий d=1,16, так как и попал в интервал (0,98-1,36), то по данному критерию нельзя сделать вывод о выполнении свойства независимости.
Необходимо вычислить коэффициент автокорреляции первого порядка:
=
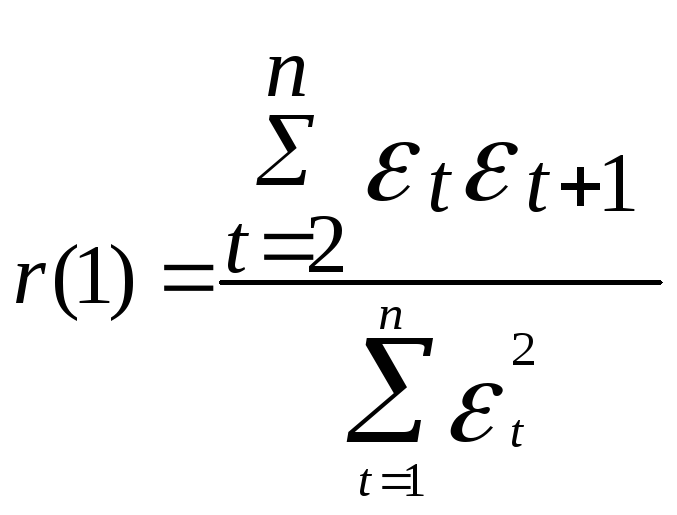0,26
фактическое
значение больше табличного. Это означает,
что в ряду динамики имеется автокорреляция,
следовательно, модель по этому критерию
неадекватна. Соответствие ряда
остатков нормальному закону распределения
определяем при помощи R/S
критерия:
.
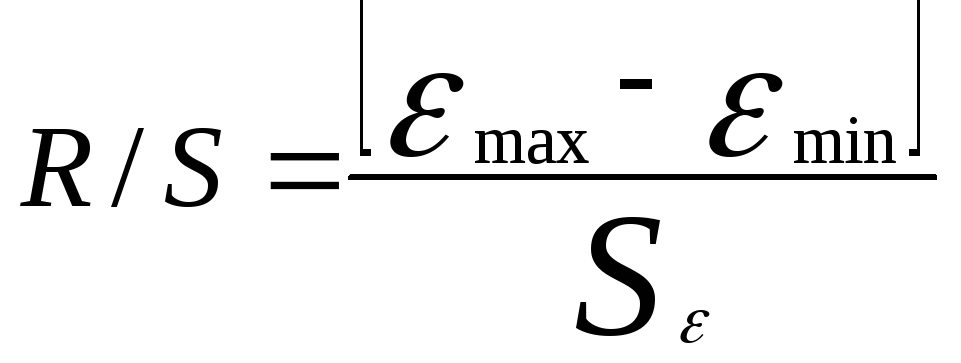Размах
вариации:
,
а среднее квадратическое отклонение
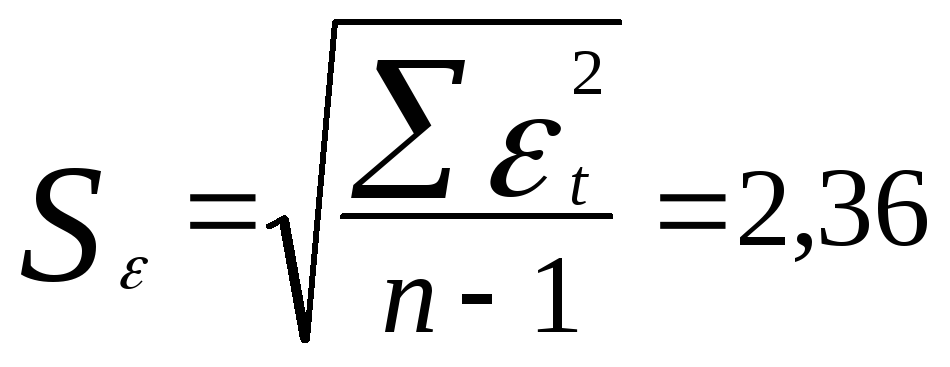
Следовательно, R/S=3,34. Это значение попадает в интервал между нижней и верхней границами табличных значений данного критерия (2,7-3,7). Следовательно, свойство нормальности распределения выполняется.
Анализ ряда остатков
|
Проверяемое свойство |
Используемые статистики |
Граница |
|
Вывод | |
|
|
наименование |
значение |
нижняя |
верхняя |
|
|
Независимость |
d-критерий Дарбина-Уотсона |
d=1,16 |
0,98 |
1,36 |
Нельзя сделать вывод по этому критерию [r(1)]>0,36 |
|
|
r(1) коэфициент автокорреляции |
-0,4 |
|
0,36 |
Неадекватна |
|
Случайность |
Критерий пиков поворотных точек |
4>2 |
2 |
|
Адекватна |
|
Нормальность |
R/Sкритерия |
2,9 |
2,7 |
3,7 |
Адекватна |
|
Вывод: модель статистически неадекватна |
|
|
| ||
4)
Оценим адекватность линейной модели
.
Модель является адекватной, если
математическое ожидание значений
остаточного ряда близко или равно нулю,
и если значения остаточного ряда
случайны, независимы и подчинены
нормальному закону распределения.
Сформулируем остаточную последовательность в таблице.
|
t |
|
|
|
Точки пиков |
|
|
( |
|
|
1 |
10 |
10,24 |
-0,24 |
- |
0,06 |
|
|
2,40 |
|
2 |
14 |
15,54 |
-1,54 |
1 |
2,37 |
1,30 |
1,69 |
11,00 |
|
3 |
21 |
20,84 |
0,16 |
0 |
0,03 |
-1,70 |
2,89 |
0,76 |
|
4 |
24 |
26,14 |
-2,14 |
1 |
4,58 |
2,30 |
5,29 |
8,92 |
|
5 |
33 |
31,44 |
1,56 |
0 |
2,43 |
-3,70 |
13,69 |
4,73 |
|
6 |
41 |
36,74 |
4,26 |
1 |
18,15 |
-2,70 |
7,29 |
10,39 |
|
7 |
44 |
42,04 |
1,96 |
0 |
3,84 |
2,30 |
5,29 |
4,45 |
|
8 |
47 |
47,34 |
-0,34 |
0 |
0,12 |
2,30 |
5,29 |
0,72 |
|
9 |
49 |
52,64 |
-3,64 |
1 |
13,25 |
3,30 |
10,89 |
7,43 |
|
∑ |
283 |
283,0 |
- |
|
44,82 |
|
52,32 |
|
)²
Проверку случайности проводим на основе критерия пиков (поворотных точек) их количество равно 4.
График
остатков линейной
модели
5) Осуществим прогноз спроса на следующие две недели.
Для построения интервального прогноза рассчитаем доверительный интервал. Ширину доверительного интервала находим по формуле:
.
.
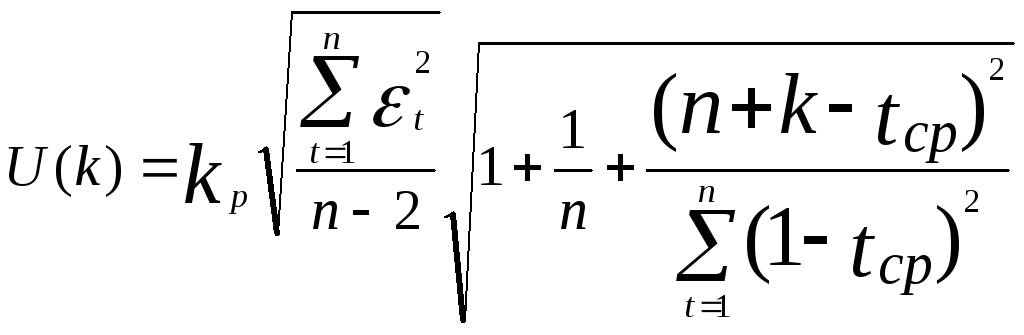Коэффициент
является табличным значением 1 –
статистическим Стьюдента. Доверительная
вероятность равна 70%,
=1,05
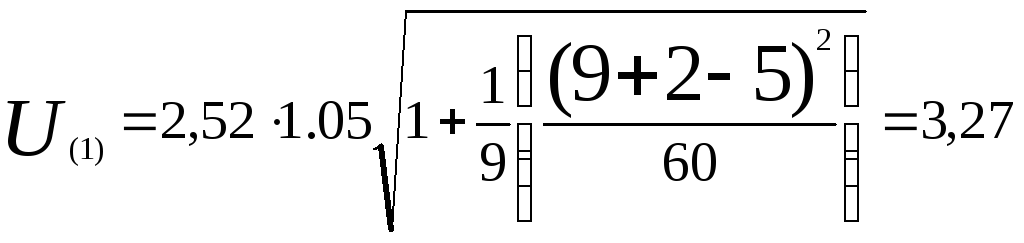
В таблице ниже сводим результаты прогнозных оценок линейной модели:
Прогнозные оценки линейной модели
|
Время(n+k) |
U(k) |
Прогноз
|
Формула |
Верхняя граница |
Нижняя граница |
|
10 |
U(1)=3,27 |
57,94 |
Прогноз+1U(1) |
61,21 |
54,67 |
|
11 |
U(2)=3,46 |
63,24 |
Прогноз+1U(2) |
66,7 |
59,78 |
6) Фактические значения показателя. Результаты моделирования и прогнозирования представляем графически.