2. Табличный способ

     На практике часто используется табличный способ задания функции. При этом способе приводится таблица, указывающая значения функции для имеющихся в таблице значений аргумента. Примерами табличного задания функции являются таблица квадратов, таблица кубов, таблица квадратных корней.

     Во многих случаях табличное задание функции оказывается удобным. Оно позволяет найти значения функции для значений аргумента, имеющихся в таблице, без всяких вычислений. На практике часто зависимость одной величины от другой находят опытным путем. В этом случае одной величине придают определенные значения, а потом из опыта для каждого из таких значений находят значение (обычно приближенное) второй величины. Таким образом опыт позволяет составить некоторую таблицу значений функции. Существуют методы, позволяющие по такой таблице подбирать формулы, задающие функции (с определенной точностью).

3. Графический способ

      Часто функция может быть задана с помощью графика..

3.Предел функции. Односторонние пределы.

Определение

Односторонний предел — предел числовой функции, подразумевающий «приближение» к предельной точке с одной стороны. Такие пределы называют соответственно левым и правым пределами.

Левый и правый пределы функции

Определение

Число называется правым пределом функции в точке , если для такое, что для любого и , выполняется неравенство (рис. 1). Правый предел обозначается 

Число называется левым пределом функции в точке , если для такое, что для любого и , выполняется неравенство (рис. 2). Левый предел обозначается 

Левый и правый пределы функции называются односторонними пределами.

Теорема

Если существуют и , причем , то существует и . Обратное утверждение также верно.

В случае, если , то предел не существует.

Задание. Найти односторонние пределы функции при 

Решение. Правый предел: 

Левый предел: 

4.Первый замечательный предел.

Первый замечательный предел:

Определение

Предел отношения синуса к его аргументу равен единице в случае, когда аргумент стремится к нулю.

Применение первого замечательного предела на практике

Пример

Задание. Найти предел 

Решение. Воспользуемся заменой и первым замечательным пределом.

Ответ. 

Пример

Задание. Найти предел 

Решение. Разложим тангенс на синус и косинус и воспользуемся свойствами пределов.

Ответ. 

Следствия из первого замечательного предела

1°   

2°   

3°   

4°   

5.Второй замечательный предел.

1

Второй замечательный предел:

здесь е - число Эйлера.

Пример

Задание. Найти предел 

Решение. Подставим , получим неопределенность и для решения предела воспользуемся вторым замечательным пределом.

Ответ. 

Следствия из второго замечательного предела

1°   

2°   

3°   

4°   

5°   

6°   

6.Непрерывность элементарных функций

Важнейшим свойством всех элементарных функций является их непрерывность в каждой точке определения. Убедимся в этом на примере некоторых элементарных функций.Рациональные функции.— непрерывна во всех точках, поскольку для любого значения аргумента.— непрерывна во всех точках, так как.— непрерывна по теореме о произведении непрерывных функций.Многочлен— непрерывен по теореме о сумме (разности) непрерывных функций.По теореме о частном непрерывных функцийдробно-рациональная функция— непрерывна везде, где.Тригонометрические функции.,— непрерывны всюду. Рассмотрим функцию.Так как, а последнее выражение стремится к нулю при, то и. Неравенствоследует из того что синус угла α (отсчитываемый от направления оси абсцисс) представляет собой величину ординаты точки на единичной окружности, а угол α есть длина дуги этой окружности.Аналогично доказывается непрерывность.По теореме о частном непрерывных функцийтригонометрические функции,— непрерывны всюду, где знаменатель не обращается в ноль.— непрерывна всюду, так как, а непрерывность приочевидна.Вычисление пределов непрерывных функцийДля непрерывных функцийзадача вычисления предела становится тривиальной. Если известно, что функциянепрерывна в некоторой точке, то ее пределв этой точке может быть вычислен нахождением значения функции в этой точке.Пример 1.Найти предел .Поскольку является непрерывной функцией, можем сразу найти предел=.Пример 2.Найти предел .И в числителе, и в знаменателе стоят непрерывные функции. Поскольку знаменатель отличен от нуля в точке , можем воспользоваться теоремой о пределе частного и записать.Пример 3.Найти предел .И в числителе, и в знаменателе стоят непрерывные функции. Поскольку знаменатель отличен от нуля в точке , можем воспользоваться теоремой о пределе частного и записать=.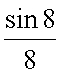