
Бикмухаметов_-_Учебное_пособие_по_МАиМУ
.pdf1
Р.Р. Бикмухаметов, Б.Г. Ктомас, С.Л.Тахаутдинова
ПОСТРОЕНИЕ ОПЕРАЦИОННОЙ И УПРАВЛЯЮЩЕЙ ЧАСТЕЙ АРИФМЕТИКО-ЛОГИЧЕСКОГО УСТРОЙСТВА С МИКРОПРОГРАММНЫМ УПРАВЛЕНИЕМ
Учебное пособие
КГТУ-КАИ 2010
2
Аннотация
В пособии рассматриваются микропрограммы и схемы в ы-
полнения основных машинных операций с фиксированной и
плавающей запятой, способы и функциональные схемы адрес а-
ции микрокоманд и кодирования сигналов микроопераций.
Пособие предназначено для использования студентами,
обучающимися по направлению «Информатика и вычислительная техника» в процессе изучения дисциплины «Машинная арифм е-
тика и микропрограммное управление»
3
Глава 1. Вводные понятия и определения.
§1.1. Арифметико-логическое устройство.
Основным понятием в курсе «Машинная арифметика и микропро-
граммное управление» является понятие АЛУ – арифметико-логического устройства для выполнения заданного набора машинных операций. АЛУ со-
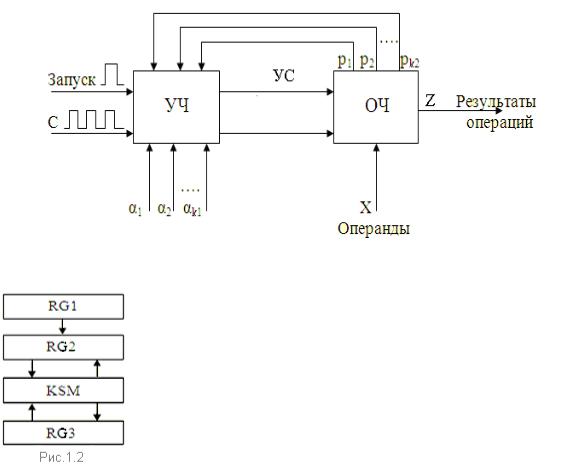
держит 2 основные части: операционную часть (ОЧ) и управляющую часть
(УЧ) в соответствии со схемой на рис. 1.1:
Рис.1.1
ОЧ - набор операционных узлов для выполнения действий по хранению и преобразованию двоичных кодов операндов,
то есть чисел, участвующих в заданных операциях. Напри-
мер, основу ОЧ в курсовом проекте по дисциплине «Ма-
шинная арифметика и микропрограммное управление» со-
ставляют три регистра (RG1, RG2, RG3) и параллельный комбинационный сумматор (KSM) (Рис.1.2). При выполнении операции сло-
жения 1-е слагаемое фиксируется в RG2, 2-е слагаемое – в RG3, сумма – в
RG2; при вычитании вычитаемое записывается в RG2, уменьшаемое – в RG3,
разность – в RG2; при умножении – множитель – в RG1, множимое – в RG3,
старшие разряды произведения – в RG2, младшие разряды произведения – в
RG1; при делении: делимое – в RG2, делитель – в RG3, частное – в RG1, ос-
таток от деления – в RG2.
4
Х – входная шина (набор проводов, по которым в ОЧ подаются двоичные коды операндов).
Z – выходная шина, на которую выдаются двоичные коды результатов опе-
раций.
УС – управляющие сигналы, формируемые в зависимости от значений осве-
домительных сигналов: p1, p2, …, pk1, 1 , 2 ,..., k 2 , где первые – это сигналы состояний узлов или элементов ОЧ, например, знаковых разрядов регистров,
а вторые - внешние сигналы, определяющие вид операции, выполняемой АЛУ в данный момент времени.
С – синхронизирующие или тактовые импульсы, которые делят время ра-
боты АЛУ на равные интервалы времени длительностью Т, называемые так-
тами. Период следования импульсов будем обозначать как Т, а длительность импульсов как τ. Тактирование требуется потому, что любая машинная опе-
рация распадается на ряд элементарных действий, называемых микроопера-
циями (МО). Примерами МО являются: суммирование двоичных кодов; ин-
вертирование всех или части разрядов кода в регистре; сдвиг кода в регистре влево или вправо, на один или несколько разрядов; запись кода в регистр;
вычитание единицы из кода, записанного в счетчике и т.д.
Втечение такта могут выполняться одна или одновременно несколько различных МО.
ВУЧ поступает также сигнал «Запуск», определяющий момент начала выполнения машинной операции.
Основу УЧ АЛУ с микропрограммным управлением составляет управ-
ляющая память (УП), т.е. запоминающее устройство, в ячейках которого за-
писываются микропрограммы машинных операций. При этом содержимое одной ячейки УП называется микрокомандой (МК) и, в общем случае, со-
держит 2 поля: операционное поле (Sоп), в котором кодируется информация об УС, формируемых в данном такте, и адресное поле (SA), определяющее адрес следующей выполняемой МК (Асл). Порядок выполнения операции оп-
5
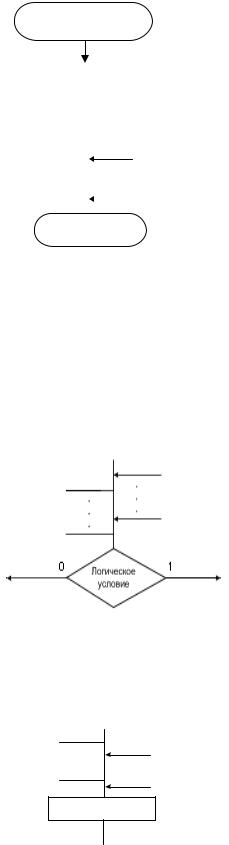
ределяется ее микропрограммой (МП), которая, как правило, задается в виде графа. Граф МП строится из вершин 4-х типов.
1. Начальная вершина, которая имеет один выход и определяет начало
выполнения МП.
НАЧАЛО
2.Конечная вершина – может иметь любое количество входов и опреде-
ляет конец выполнения МП.
|
|
|
. |
|
. |
. |
|
|
|
. |
|
. |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
КОНЕЦ
3.Условная вершина – может иметь любое количество входов и два вы-
хода, помеченных цифрами 0 и 1. В поле вершины указывается логиче-
ское условие (ЛУ), проверяемое в данном такте работы АЛУ. При вы-
полнении ЛУ выход из вершины производится по стрелке, помеченной цифрой 1, и наоборот. В качестве ЛУ используются значения осведо-
мительных сигналов и любых переключательных функций от них.
4.Операторная вершина – может иметь любое количество входов и один выход и определяет совокупность МО, выполняемых в данном такте.
. |
. |
|
. |
||
. |
||
. |
||
. |
||
|

6
Требования к графу МП:
для любой вершины в графе МП должен быть хотя бы один путь к конечной вершине;
каждый выход должен соединяться только с одним входом;
каждый вход должен соединяться, по крайней мере, с одним выхо-
дом.
Перейдем далее к основному материалу по микропрограммам и опера-
ционным схемам выполнения арифметических операций над двоичны-
ми числами с фиксированной и плавающей запятой.
§1.2. Форма представления чисел с фиксированной запятой.
В этом случае положение запятой в машинных кодах операндов фик-
сировано и не меняется в процессе вычислений. Например, выделяется m разрядов под целую часть и n разрядов под дробную часть чисел.
Условно это представляется в виде разрядной сетки процессора, где квадратики обозначают двоичные разряды:
Здесь qi [-n ≤ i ≤ (m-1)] означает двоичный разряд с весом, равным 2i ; qm- знаковый разряд, не имеющий никакого веcа; 0 в этом разряде означает
«плюс», 1 – «минус».
Перечислим особенности данной формы.
1) Числа могут представляться в прямом или дополнительном кодах.
Прямой код числа Q – это обычная запись числа со своим знаком. m-1
Qпр = qmqm-1qm-2......q-n = ± Σ qi 2i i=-n
Например, пусть m = 3, n = 4 |
Зн, |
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Если Q = + 3⅜ = +11,011, то Qпр = |
0 |
0 |
1 |
1 |
, |
0 |
1 |
1 |
0 |
|||||
Если Q = – 3⅜ = – 11,011, то Qпр= |
1 |
0 |
1 |
1 |
, |
0 |
1 |
1 |
0 |
|||||

7
Если Q= – 69⁄16= – 110,1001, Qпр= 1 1 1 0 , 1 0 0 1
В дополнительном коде вместо знакового разряда используется дополни-
тельный старший разряд dm с отрицательным весом, равным ( – 2m). m–1
Qдоп= dmdm-1dm-2…d-n = dm (–2m) + Σ di 2i i =-n
Правила получения дополнительного кода.
dm
0. | Q | = Qпр , если Q ≥ 0
Qдоп=
1. |Q| + 2-n , если Q < 0
Так как значение дополнительного разряда dm числа в дополнительном коде совпадает со значением знакового разряда qm числа в прямом коде, то в литературе, для удобства, разряд dm всѐ равно называют знаковым, хотя по сути это разряд с отрицательным весом.
В арифметических операциях над дополнительными кодами знаковые разряды участвуют наравне с остальными разрядами, то есть формально
(или условно) их рассматривают как обычные старшие разряды соответст-
вующих двоичных чисел, имеющие вес (+2m). А так как, по сути, это разряды с отрицательным весом, то результаты операций приходится в нужных слу-
чаях корректировать. Например, если сложить дополнительные коды слагае-
мых вместе со знаковыми разрядами, то получится дополнительный код ал-
гебраической суммы, если отбросить единицу переноса из знакового разряда, имеющую вес, равный 2m+1.
Например, пусть m=3, n=3, F=C+D, C= 6 12 110,1 , D= 7 85 111,101. Тогда:
Сдоп |
1 0 0 1, |
1 0 0 |
|||||
Dдоп |
+ 0 1 1 1, |
1 0 1 |
|||||
|
0 |
0 |
0 |
1, |
0 |
0 |
1 |
Fдоп ( 1 18)доп
При анализе результатов операций над дополнительными кодами используют формальные правила получения дополнительного кода:

8
|
зн |
|
|
|
||||||||||||||
|
0. |
|
Q |
|
|
|
Q |
|
,если Q>=0 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Qдоп |
|
|
|
2 n 2m |
|
2 n 2m (2m 2 n |
|
) 2 n 2m 1 |
|
|
,если Q<0 |
|||||||
|
1. |
Q |
Q |
Q |
Q |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||
Таким образом, дополнительный код отрицательного числа можно по-
лучить как дополнение модуля числа до 2m+1, почему, собственно, код и на-
зывается дополнительным.
Так как знаковые разряды суммируются наравне с остальными разря-
дами, то усложняется обнаружение переполнения разрядной сетки (ПРС),
признаком которого при суммировании модулей чисел является наличие единицы переноса Пm из старшего разряда комбинационного сумматора
(KSM), имеющей вес, равный 2m.
Докажем, что при суммировании дополнительных кодов может ис-
пользоваться один из трех признаков ПРС.
1.Знаки C и D совпадают, но не совпадают со знаком F.
2.Переносы в знаковый разряд Пm и из знакового разряда Пm+1 не совпадают, т.е. Пm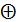 Пm+1 = 1.
Пm+1 = 1.
3.При модификации кода два знаковых разряда F не совпадают. Моди-
фикация кода означает использование не одного, а двух знаковых раз-
рядов, в которых код 00 означает «плюс», а 11 – «минус».
Доказательство. В дополнительном коде числа меняются в диапазоне от (-2m)
до (2m-2-n). Следовательно, ПРС возникает, если:
|
2m F 2m |
(1.1) |
|
Пусть F=C+D. Тогда ПРС возможно лишь при одинаковых знаках слагаемых. |
|||
п.1. С>0 и D>0, |
и есть ПРС. Тогда при суммировании Cдоп и Dдоп Пm=1, так |
||
как, согласно (1.1), │С│+│D│≥2m. |
Следовательно, в знаковых разрядах сум- |
||
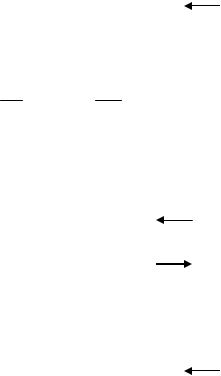
мируемых кодов будет наблюдаться следующая ситуация: |
|||
|
зн |
|
|
|
0 |
|
|
+ |
|
Пm=1 |
|
|
0 |
|
|
|
1 |
(При этом Пm+1=0) |
|
9
Как видно, первые два признака имеют место.
При модификации кода, т. е. при использовании двух знаковых разрядов имеем:
знаки
00
+ |
Пm=1 |
00
01 Знаковые разряды не совпадают.
п.2 C<0, D<0 и есть ПРС. Тогда при суммировании Cдоп и Dдоп Пm=0, так как
(│С│+2-n +(│D│+2-n) = (2m −│C│) +(2m −│D│) = [2m+1−(│C│+│D│)] < 2m
(согласно (1.1)(│C│+│D│) > 2m. Следовательно:
зн |
|
1 |
|
+ |
Пm=0 |
1 |
|
1 0 |
Пm+1=1 |
При модификации кода: |
|
знаки |
|
11 |
|
+ |
Пm=0 |
11
10 Знаки не совпадают
Если F=C−D, то ПРС может быть при С > 0 и D < 0 (см. п.1), либо при С < 0 и
D > 0 (см. п.2).
Перейдем далее к примерам записи чисел в прямом, дополнительном и модифицированном дополнительном кодах для двух вариантов фиксации за-
пятой, используемых в современных процессорах. В первом варианте n=0, во втором - m=0.
Примеры оформлены в виде таблицы 1.1, в которой m = 3 для первого варианта и n=3 для второго варианта фиксации запятой. Например, в верхней строке таблицы число Q=+5,5 во втором варианте вызывает ПРС, а в первом варианте округляется до n разрядов после запятой по следующему правилу: к (n+1) разряду прибавляется единица, затем (n+1) - й и все более младшие разряды после запятой отбрасываются.
10
Таблица 1.1
|
|
|
|
|
|
m=3,n=0 |
|
m=0,n=3 |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Q |
|
|
зн |
|
|
|
, |
|
зн |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
' |
|
|
|
|
||
|
|
|
|
|
|
Qпр |
|
Qдоп |
Qмод.доп. |
Qпр |
|
|
Qдоп |
|
Qмод.доп. |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
+5,5 |
0110 |
|
0110 |
|
|
00110 |
ПРС |
|
|
ПРС |
|
ПРС |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
-5,25 |
1101 |
|
1011 |
|
|
11011 |
ПРС |
|
|
ПРС |
|
ПРС |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
+8 |
|
|
ПРС |
|
ПРС |
ПРС |
ПРС |
|
|
ПРС |
|
ПРС |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
-8 |
|
|
|
ПРС |
|
1000 |
|
|
11000 |
ПРС |
|
|
ПРС |
|
ПРС |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
-1 |
|
|
|
1001 |
|
1111 |
|
|
11111 |
ПРС |
|
1000 |
|
|
11000 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
+1 |
|
|
0001 |
|
0001 |
|
|
00001 |
ПРС |
|
|
ПРС |
|
ПРС |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
+0 |
|
|
0000 |
|
0000 |
|
|
00000 |
0000 |
|
0000 |
|
|
00000 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
-0 |
|
|
|
1000 |
|
0000 |
|
|
00000 |
1000 |
|
0000 |
|
|
00000 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
1 |
|
|
0001 |
|
0001 |
|
|
00001 |
0100 |
|
0100 |
|
|
00100 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
1 |
|
|
1001 |
|
1111 |
|
|
11111 |
1100 |
|
1100 |
|
|
11100 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
3 |
|
|
0000 |
|
0000 |
|
|
00000 |
0011 |
|
0011 |
|
|
00011 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
3 |
|
|
1000 |
|
0000 |
|
|
00000 |
1011 |
|
1101 |
|
|
11101 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
3 |
|
0000 |
|
0000 |
|
|
00000 |
0010 |
|
0010 |
|
|
00010 |
|||||
16 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
3 |
|
1000 |
|
0000 |
|
|
00000 |
1010 |
|
1110 |
|
|
11110 |
|||||
16 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
3 |
|
0000 |
|
0000 |
|
|
00000 |
0001 |
|
0001 |
|
|
00001 |
|||||
32 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
3 |
|
1000 |
|
0000 |
|
|
00000 |
1001 |
|
1111 |
|
|
11111 |
|||||
32 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
+ |
5 |
|
0011 |
|
0011 |
|
|
00011 |
ПРС |
|
|
ПРС |
|
ПРС |
||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
5 |
|
|
0001 |
|
0001 |
|
|
00001 |
0101 |
|
0101 |
|
|
00101 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
