Бикмухаметов_-_Учебное_пособие_по_МАиМУ

51

Контрольные вопросы.

1.Почему в начале умножения RG2 сбрасывается в 0?

2.Как изменяется результат умножения, если в способах 2 и 4 не сбрасы-

вать RG2 в начале умножения?

3.Почему нельзя совмещать в одном такте МО сложения и сдвига в спо-

собах 1 и 3?

4.Зачем сдвигается RG1 в способах 2, 3 и 4?

5.Почему при округлении в способе 1 единица прибавляется к n-му, а не

к(n+1)-му разряду после запятой?

6.Почему при суммировании перенос П0 запоминается в RG2(0)?

7.Почему результат умножения целых чисел приводится к двойному формату?

8.Каким образом используется связь из RG1 в RG2?

9.C какой целью в схему вводится дополнительный триггер знака Тзн?

10.Почему триггера переноса Тпер нет в схеме умножения в прямом коде?

11.Когда перенос Пm требуется запоминать в RG2(m)?

12.Когда требуется использовать цепи инверсной подачи разрядов RG3 в

KSM?

52

Глава 4. МП и схемы деления чисел с фиксированной запятой

( G ⁄ E = F с остатком B).

§4.1. Деление дробей в прямом коде.

В разрядной сетке для дробей:

Gпр= g0 ,g−1g−2…g−n; Епр= е0 ,e−1e−2…e−n; Fпр= f0 ,f−1f−2…f−n, где g0,e0,f0-знаки.

Правила.

1)Остаток B по окончании деления не сохраняется и не выдается на вы-

ходную шину Z.

2)f0 = g0e0

3)При делении ПРС не будет, если |G| ⁄ |E| < 1 или |G|−|E| < 0

4)Деление сводится к циклическому вычитанию делителя из удвоенных частичных остатков (ЧОС) требуемое количество раз.

Вкаждом цикле деления определяется одна цифра частного. Например, разделим вручную |G|=11⁄16= 0,1011 на |Е|=7⁄8= 0,111, считая, что n = 4.

Здесь в каждом цикле ЧОС удваивается, т.е. справа приписывается 0 (в

1-м цикле удваивается делимое). Если полученное число ≥|E|, то в частном ставится1, и из полученного числа вычитается |E|, иначе в частном ставится

0. В частном формируются (n + 1) разрядов, т.е. на 1 разряд больше для ок-

ругления |F|. К этому разряду прибавляется 1, затем этот разряд отбрасывает-

ся.

Как видно, в каждом цикле деления вручную, во-первых, ЧОС удваива-

ется; во-вторых, полученное число сравнивается с |E|. При машинном деле-

нии первая операция реализуется путем сдвига влево, вторая – путем вычи-

тания и анализа знака разности.

Обозначим через Gi - ЧОС в i-ом цикле деления (i= 1÷n+1).

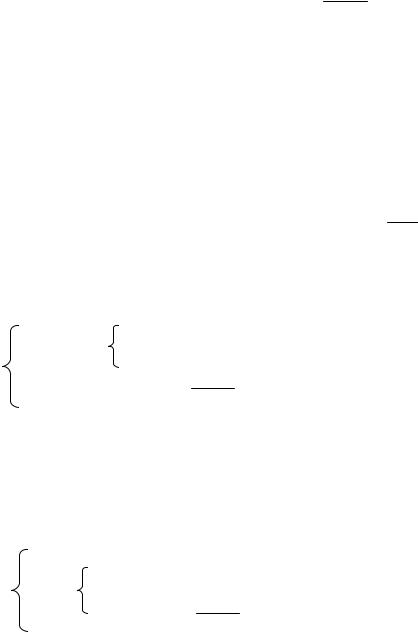
53

Перед началом деления выполняется проверка на ПРС:|G|−|E|= G0; если G0≥0,

то деление не выполняется; если G0<0, то делить можно. Тогда:

1)восстанавливается делимое: G0+|E|= |G|;

2)удваивается делимое: 2(G0+|E|);

3)формируется ЧОС G1= 2(G0+|E|) −|E| .

По знаку G1 определяется 1-я цифра |F|: f−i= зн.G1 .

В остальных циклах выполняются аналогичные действия, т.е.:

Gi = 2Gi−1− |E|, если Gi−1 ≥ 0 .

Если же Gi−1 < 0, то:

1)восстанавливается предыдущий остаток: Gi−1+ |E|;

2)удваивается предыдущий остаток: 2(Gi−1+ |E|);

3)формируется ЧОС : Gi = 2(Gi−1+ |E|) − |E| .

По знаку Gi определяется очередная цифра |F|: f−I = зн.Gi .

Деление дробей в прямом коде без восстановления остатка.

В алгоритме деления с восстановлением остатка ЧОС Gi = 2Gi−1 − |E|, если Gi−1 ≥ 0 ;

2(Gi−1+ |E|) − |E|, если Gi−1< 0 ;

Цифра частного f−I = зн.Gi

Недостаток алгоритма в том, что в цикле деления выполняется либо 1, либо 2

МО суммирования. Можно ускорить деление, если использовать алгоритм деления без восстановления остатка, который получается, если во 2-й строке предыдущего алгоритма раскрыть скобки

Gi = 2Gi−1− |E|, если Gi−1 ≥ 0 ;

2(Gi−1+ |E|) − |E|= 2Gi−1+ 2|E|− |E|=2Gi−1+|E|, если Gi−1< 0

Цифра частного f−i = зн.Gi

Здесь, если Gi−1< 0, то можно, не восстанавливая предыдущий остаток, удво-

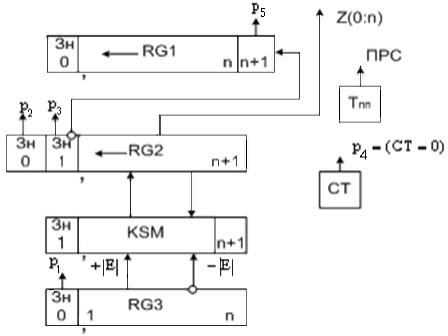
ить текущий остаток и прибавить к нему |E| . Данный алгоритм реализуется ОС на рис.4.1.

54

Рис. 4.1.

55

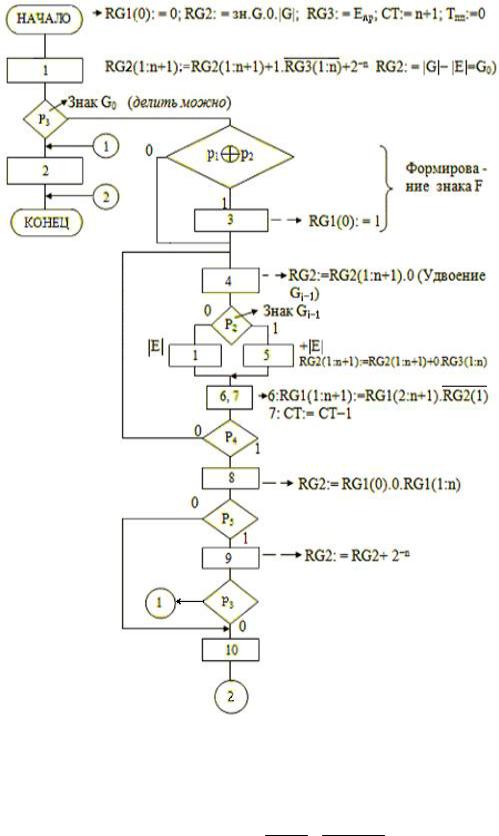
Рис. 4.2

В графе МП на рис.4.2. в каждом из (n+1) циклов деления RG1(1:n+1) сдви-

гается влево с вводом в младший разряд очередной цифры частного f−I = зн.Gi = RG2(1)

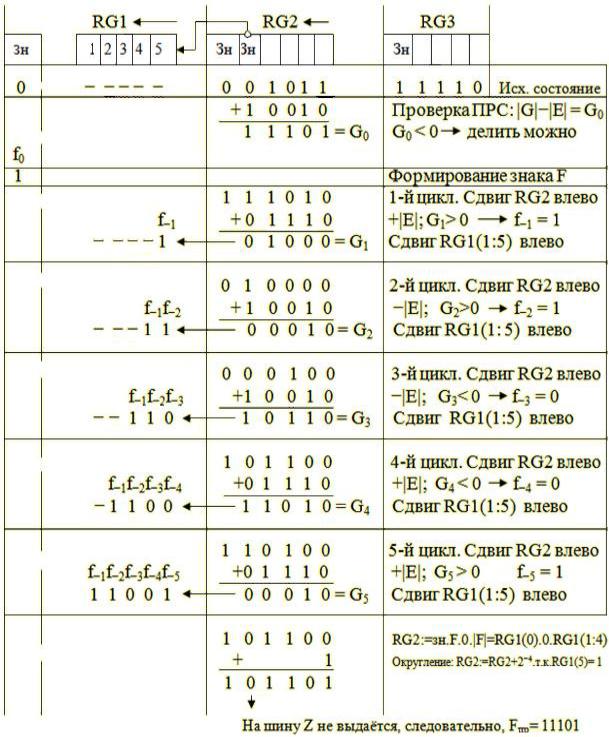
Построим далее таблицу состояний регистров ОС деления, считая, что n =4, G = +11⁄16 , E = − 7⁄8 .

Здесь Gпр = 01011, Епр = 11110 , Fпр = fo , f−1f−2f−3f−4f−5

56

§4.2. Деление целых чисел в прямом коде.

В разрядной сетке для целых чисел:

Епр= emem−1…e0 ; Fпр= fmfm−1…f0 ; Gпр= g2m+1g2m…g0 ; Bпр= bmbm−1…b0 ,

где fm = em 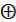g2m+1 ; bm = g2m+1 .

57

Z(m:0)

Рис. 4.3

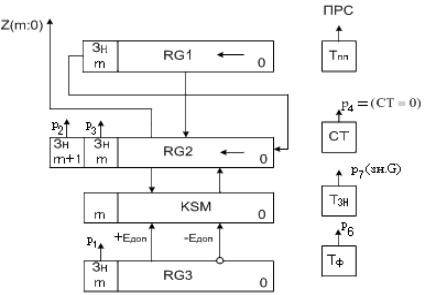
ОС на рис.4.3. характеризуется тремя отличиями от схемы деления дробей.

1)Делимое представляется в двойном формате и вводится в 2 регистра:

(m+1) старших разрядов Gпр в RG2(m:0), (m+1) младших разрядов в

RG1. Соответственно изменены цепи сдвига в RG1 и RG2.

Вкаждом цикле деления оба регистра одновременно сдвигаются влево с вводом 0 в RG1(0). Как и ранее, в RG1(0) формируется очередная

цифра частного, но не в процессе сдвига, а после сдвига. Этот разряд

устанавливается, если текущий ЧОС Gi ≥ 0, иначе в этом разряде со-

храняется 0.

2)Остаток B выдается на выходную шину Z. При этом ему присваивается знак G, т.е. машинное деление выполняется с недостатком.

3)Проверка на ПРС выполняется в 2 этапа.

1-й этап. Епр и Fпр меняются в диапазоне от –(2m−1) до +(2m−1) . Следователь-

но, |G| не может превосходить (без учета остатка) величины

|E|max×|F|max= (2m −1)(2m −1) = 22m − 2(m+1)+1,

которая меньше числа 22m . Последнее означает, что 2-й разряд слева в Gпр ,

представленном в двойном формате, должен быть равен 0, что и проверяется на 1-м этапе.

58

2-й этап. В процессе деления ПРС не будет, если |G| ⁄ |E| < 2m или

|G| − |E|2m= G0< 0. Для получения G0 делимое сдвигается влево на 1 разряд, и

из RG2(m:0) вычитается |E| . Так как делитель оказывается при этом сдвину-

тым относительно делимого на m разрядов влево, в RG2(m:0) и RG1(m:1)

формируется разность |G|−|E|2m= G0 . Если G0≥ 0, то Тпп устанавливается , и

деление не выполняется. Если G0< 0, то делить можно. Тогда в RG1(0) фор-

мируется знак F, т.е. этот разряд устанавливается, если знаки G и E разные.

Далее m раз выполняется цикл деления. В каждом i-ом цикле (i=1÷m), во-

первых, Gi−1 в RG2 сдвигается влево. Во-вторых, формируется текущий ЧОС

Gi . Для этого либо из RG2(m:0) вычитается |E|, если Gi−1≥ 0, [т.е., RG2(m+1)

= 0], либо к RG2(m:0) прибавляется |E|, если Gi−1 < 0, [т.е., RG2(m+1)=1] . В-

третьих, формируется цифра частного fm−i= зн.Gi [RG1(0):=1, если Gi≥0].

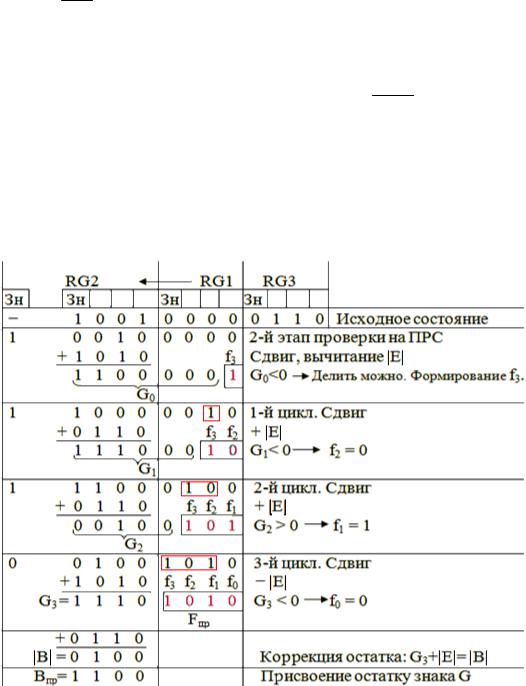
Построим таблицу состояний регистров ОС деления, считая, что m=3, G = −16, E = +6. Здесь Gпр=10010000, Eпр= 0110, Fпр=f3f2f1f0= 1010 и Впр=1100 .

На 1-м этапе проверки на ПРС убеждаемся в том, что 2-й разряд слева в Gпр

равен 0.

59

Если частное четное, то остаток в последнем цикле Gm=G3=(|B|−|E|)доп<0,

т.е. требуется коррекция остатка. Для этого, если Gm<0, к нему прибавля-

ется |E| . Если частное нечетное, то Gm= |B|, что и требуется.

§4.3. Деление целых чисел в дополнительном коде

Пусть Fдоп= φm φm−1… φ0

При делении в дополнительном коде знаки участвуют в операции наравне с остальными разрядами, поэтому правила деления формулируются в более общем виде.

В i-ом цикле деления ( i = 1÷ m+1)

Gi−1− Eдоп 2m+1−i, если знаки Gi−1 и Е одинаковые,

Gi =

Gi−1+ Eдоп 2m+1−i, если знаки Gi−1 и Е разные.

1, если знаки Gi и Е одинаковые

Цифра частного φm+1−i =

0, если знаки Gi и Е разные.

Особенности.

1.В первом цикле формируется знак частного φm+1−i = φm , а Gi−1=G0=Gдоп. 2.Частное формируется в прямом коде, если знаки G и E одинаковые, и в обратном коде, если разные. А так как при F<0 Fдоп=Fобр+1, то, следовательно, при разных знаках G и E требуется коррекция частного (+1). Однако тот факт, что 0 в дополнительном коде всегда формируется со знаком «плюс»,

усложняет правила коррекции, а именно, приводит к тому, что при G<0,E>0

и B=0 результат оказывается увеличенным на 1, а при G<0, E<0 и B=0 –

уменьшенным на 1. В результате частное увеличивается на 1, если: а)

G>0,E<0; б)G<0, E>0 и B≠0; в) G<0,E<0 и В=0.

3.Проверка на ПРС выполняется в 2 этапа.

1-й этап. Едоп и Fдоп меняются в диапазоне от (−2m) до +(2m−1). Следовательно, Gmax(без учѐта остатка) = (−2m) · (−2m) = 22m=010…0 (двойной формат) . Во всех остальных допустимых случаях |G| < (2m)(2m−1)=22m −2m < 22m, что означает совпадение двух старших разрядов Gдоп . Таким образом, только в одном допустимом случае, когда Е = F =−2m, два старших разряда Gдоп не

60

совпадают, в остальных допустимых случаях совпадают, что учитывается на

Проверка по условиям (4.1÷4.4) совмещается с 1-м циклом деления.

ОС на рис. 4.4 характеризуется следующими отличиями от схемы деления в прямом коде:

1.В KSM подаются все разряды RG3, включая знак, т.е. сложение и вычита-

ние выполняются по способу 1а.

2.Введен флажковый триггер Тф , который определяет первый цикл деления,

т.е. Тф=1 только в 1-м цикле. Также после окончания циклов деления Тф: = 1,

если В = 0.

Рис. 4.4

В МП на рис. 4.5. предполагается, что : RG3:=Eдоп; RG2(m:0):=(m+1) старших разрядов Gдоп ; RG1:=(m+1) младших разрядов Gдоп ; Tпп:=0 ;

Tф: =1; Тзн:=знG; 1-й этап проверки на ПРС выполнен.

В графе МП проставлены номера следующих МО:

МО1: RG2 :=RG2(m:0).RG1(m); RG1:=RG1(m−1:0).0 (сдвиг влево Gi−1);