
Бикмухаметов_-_Учебное_пособие_по_МАиМУ
.pdf
11
В таблице 1.1 следует обратить внимание на то, что ноль в дополни-
тельном коде всегда формируется со знаком «плюс».
2).Если количество разрядов после запятой больше n, то выполняется округ-
ление до n разрядов, например, по следующему правилу: к (n+1)-му разряду после запятой прибавляется единица, затем (n+1)-й и все более младшие раз-
ряды отбрасываются. В результате погрешность представления чисел стано-
вится знакопеременной и не накапливается при многократных операциях над числами.
3).Если количество разрядов до запятой больше m, то возникает переполне-
ние разрядной сетки (ПРС). В этом случае вычисления прерываются, так как у числа теряются старшие разряды.
4).В современных процессорах используют два варианта фиксации запятой в разрядной сетке. Один из вариантов используется для представления целых
чисел в разрядной сетке вида |
Зн |
|
0 , |
m |
m-1 |
Зн
другой – для дробей в сетке вида 0, 1 n .
Первый вариант используется в командах целочисленной арифметики и для представления порядков чисел с плавающей запятой; второй – для представ-
ления мантисс чисел с плавающей запятой.
Контрольные вопросы.
1.С какой целью выполняется округление?
2.Почему при ПРС выполняется останов вычислений?
3.Для чего предназначены входная и выходная шины ОЧ АЛУ?
4.Сколько МО могут выполняться в течение одного такта?
5.Для чего нужны синхронизирующие сигналы?
6.Что записывается в поле условной вершины графа МП?
7.Что такое обратный код числа?
8.Что такое дополнительный код числа?
12
Глава 2. Микропрограммы и операционные схемы выполнения алгебраического сложения-вычитания чисел с фиксированной запятой
( А = С ± D ).
§2.1. Сложение-вычитание в прямом коде.
Исходные данные.
1).Алгоритмы сложения-вычитания не зависят от положения запятой в раз-
рядной сетке. Далее для определенности используем вариант целых чисел
(n=0)
2).Алгоритмы сложения-вычитания можно классифицировать следующим образом:
Способ 1. С, D поступают в дополнительном коде, F выдается в дополни-
тельном коде.
Способ 2. С, D и F представляются в прямом коде, а при суммировании в нужных случаях могут переводиться в дополнительный код оба операнда.
Способ 3. С, D и F представляются в прямом коде, а при суммировании в нужных случаях может переводиться в дополнительный код только один из операндов.
В каждом из этих способов может использоваться любой из трех ва-
риантов устройства сложения-вычитания:
а) в KSM – один знаковый разряд;
б) в KSM - два знаковых разряда;
в) в KSM - нет знакового разряда, а о знаке получающегося результата судят по переносу из старшего разряда KSM (Пm) Здесь и далее Пi будет означать перенос на входе i-го разряда KSM.
Таким образом, получаем 9 вариантов алгоритмов, из которых практическое значение имеют 5 алгоритмов или способов: 3в, 1а, 1б, 2а, 2б.
3).Далее будет использоваться основная формула машинной арифметики, со-
гласно которой, если инвертировать разряды модуля числа | X | и прибавить
13
единицу младшего разряда (2n), то получим дополнение модуля | X | до це-
лой степени двойки (2m) |
|
X + 2-n = 2m – | X | |
( 2.1) |
Способ 3в. (сложение-вычитание в прямом коде чисел, поступающих в пря-
мом коде).
п.1. Если знаки С и D одинаковые, то сложение остается сложением, вычи-
тание – вычитанием. Если знаки C и D разные, то сложение заменяется вычи-
танием, а вычитание – сложением.
п.2. Если по результатам п.1 требуется сложение, то F = знак С( | С | + | D | )
Если при суммировании Пm= 1, то это естественный признак ПРС.
п.3. Если по результатам п.1 требуется вычитание, то, согласно школьному
алгоритму: F = знак С( | С| – |
| D | ), если | С| ≥ | D | ; |
|
знак D ( | D | – |
| C | ), если | С | < | D |; |
(2.2) |
На практике различают два подхода для реализации правил ( 2.2).
Подход 1. Используется специальная схема сравнения │C│ и │D│ для опре-
деления большей величины. Затем к большей прибавляется дополнение до 2m
меньшей величины. Если при этом Пm=1, то эта единица переноса с весом 2m
отбрасывается. Формально это записывается как суммирование по модулю
2m
Например, пусть │C│≥│D│. Тогда выполняются действия:
Знак F : = знак С |
|
|
(2.3) |
|
[| C| + 2m – | D | ] (mod2m) = [согл.(2.1)]=(│C│+│D│+2-n) (mod2m) |
||||
Можно показать, что последний результат равен | C | – | D |. |
||||
Действительно, |
| C | +(2m– |D | ) = 2m+ (| C| – |
| D | ) ≥ 2m , то есть, при сумми- |
||
ровании Пm= 1. |
Отбрасывая эту единицу, то есть, уменьшая результат на 2m, |
|||
получаем искомый результат │C│ – │D│ .
Аналогичное доказательство при | C | < | D | .
14
Пример: m=3, n=0, F = C + D, С=+2, D = – 6
Зн |
|
|
|
|
|
|
|
|
Cпр = 0 0 1 0 |
101 2m–| C | =| C |
| + 1 |
||||||
|
|
|
|
+ 1 |
|
|
|
|
Dпр= 1 |
1 1 0 |
|
110 |
|
Зн |
|||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
100 = Fпр = 1100 |
||||
|
|
|
|
Пm=1 |
|
|
|
|
|
|
|
|
|
|
|
||
Подход 2. Используется вариант алгоритма «наугад». В алгоритме наугад считается, что |C|≥|D|, и выполняются действия (2.3). Но если |C|<|D|, то ре-
зультат суммирования P=|C|+2m–|D|=2m–(|D|–|C|)<2m,т .е.,Пm=0, и вместо тре-
буемой разности |D|–|C| получается ее дополнение до 2m. Тогда выполняется коррекция: P+2-n = [(согл.(2.1)] = 2m–P=2m–2m+|D|–|C|=|D|–|C|. Знак при этом меняется на противоположный. Таким образом, если Пm=0, то все разряды результата, включая знак, инвертируются, и к младшему разряду прибавляет-
ся единица. Пример: m=3, n=0, F=C–D, С= –2, D= –5
010 |С|
010 + 1 1 101
0 010
+1
0 011 = Fпр
Операционная схема (ОС) сложения-вычитания по способу 3в (наугад).
ОС включает 2 регистра (RG2, RG3) из числа трех регистров, рассмотренных
ранее; KSM; триггер переноса (Тпер) для запоминания значения Пm; триггер переполнения (Тпп), устанавливаемый при обнаружении ПРС, и УЧ (рис. 2.1).

15
Рис. 2.1.
Здесь X(m:0) – входная шина, т.е. набор из (m+1) проводов, по которым по-
ступают значения разрядов операндов (Спр в RG2, Dпр в RG3).
Z(m:0) - выходная шина, на линии которой выдаются разряды результата
(Fпр). |
|
|
Сигналы состояний, поступающие в УЧ: |
|
|
p1 |
= RG2(m) = знак С |
|
p2 |
= RG3(m) = знак D |
|
p3 |
= Тпер= Пm |
1, если сложение |
Также в УЧ поступает внешний сигнал α = |
0, если вычитание |
|
Работа схемы описывается содержательным графом МП, в операторных вершинах которого приводятся записи соответствующих МО. Допускается в операторных вершинах проставлять лишь номера выполняемых МО, предва-
рительно составив список используемых МО. Например, пусть 1-я МО – это сброс Тпп и запись Спр в RG2, 2я МО – запись Dпр в RG3, что записывается как: МО1:Тпп:=0; RG2:=X; МО2: RG3: =X
Также в список используемых МО войдут следующие МО.
MO3: RG2(m–1: 0): = RG2(m–1:0)+RG3(m–1:0);
Тпер : = Пm
МО4: RG2(m–1:0):= RG2(m–1:0)+RG3(m–1:0)+2-n;
Тпер : = Пm
МО5: Тпп: = 1
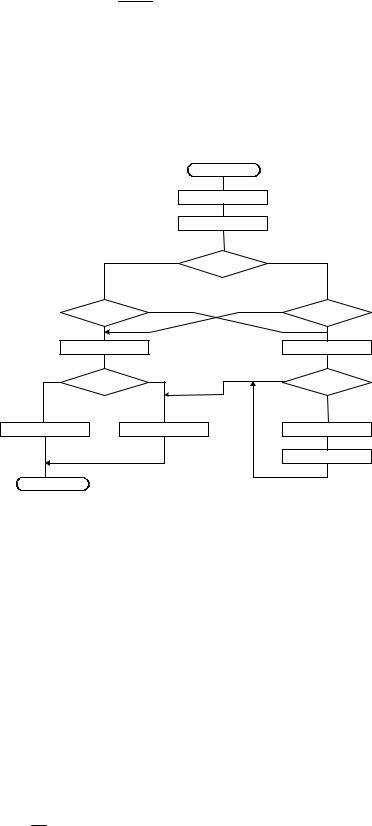
16
МО6: RG2: = RG2
МО7: RG2: = RG2+2-n
МО8: Z : = RG2 (МО выдачи Fпр из RG2 на выходную шину Z); Тогда содержательный граф МП можно представить в виде, пока-
занном на рис.2.2
|
|
|
|
Начало |
|
||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
0 |
p1 |
p |
1 |
|
|
|
|
|
2 |
|
||
|
|
0 |
|
|
0 |
|
|
|
|
|
|
|
|||
|
1 |
|
|
|
|
|
1 |
|
3 |
|
|
|
|
4 |
|
1 |
p |
|
0 |
|
|
1 |
p3 |
|
|
|
|
|
|||
|
3 |
|
|
|
|
||
|
|
|
|
|
|
|
0 |
5 |
|
|
8 |
|
|
|
6 |
7
конец
Рис.2.2.
§2.2. Сложение-вычитание в дополнительном коде.
Способ 1а. (Сложение-вычитание в дополнительном коде чисел, поступаю-
щих в дополнительном коде).
Правила.
1)Если F=C+D, то Fдоп= (Сдоп+ Dдоп)(mod2m+1). Сумма дополнительных ко-
дов слагаемых равна дополнительному коду алгебраической суммы,
если единица переноса из знакового разряда отбрасывается (т.е. сум-
мирование выполняется по mod2m+1).
2)Если F=C–D, то F=C=(–D). Тогда Fдоп=[(Cдоп+(–D)доп](mod2m+1)= =(Cдоп+Dдоп +2-n)(mod2m+1). Здесь вычитание сводится к сложению путем изменения знака D на противоположный. А если инвертировать знак числа, пришедшего в дополнительном коде, то, по правилам полу-
чения дополнительного кода, должны быть инвертированы и остальные

17
разряды числа, а к младшему разряду должна быть прибавлена едини-
ца.
Пример. m=3, n=0, F=C–D, C= –5, D= +2
Сдоп= 1 011 |
1 011 |
Сдоп |
|
Dдоп= 0 010 |
+1 101 |
(Dдоп+2-n) |
|
|
|
1 |
|
|
1 001 |
= Fдоп |
|
В отличие от способа 3в, здесь знаки участвуют в операции суммиро-
вания. Поэтому иначе выявляется ПРС.
Признаки переполнения:
1)Знаки С и D совпадают, но не совпадают со знаком суммы.
2)Перенос в знаковый разряд Пm и из знакового разряда Пm+1 не совпада-
ют, т.е.: Пm Пm+1 = 1
Пm+1 = 1
Преимущественно используется второй признак, т.к. в первом случае нужно
хранить знаки С и D до конца операции суммирования.
Операционная схема (без цепей записи в RG2 и RG3, Тпп и УЧ)
|
|
p1 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
Tпер |
|
|
|
|
|
Z(m:0) |
|||||
|
|
|
|
||||||||
|
|
|
|
|
зн |
|
|
RG2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
m |
|
m-1 |
0 |
|||
|
|
|
|
|
|
|
|
||||
|
МM2 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
||||
|
|
|
|
П m 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
KSM |
0 |
|||||||
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
П m |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
зн |
|
|
RG3 |
|
|
|
|
|
|
|
|
m |
|
m-1 |
0 |
|||
|
|
|
|
|
|
|
|
||||
Рис. 2.3.
Исходя из приведенных правил, получаем следующие содержательный
граф МП и список МО. В комментариях к начальной вершине записаны
уже выполненные МО (рис. 2.4):
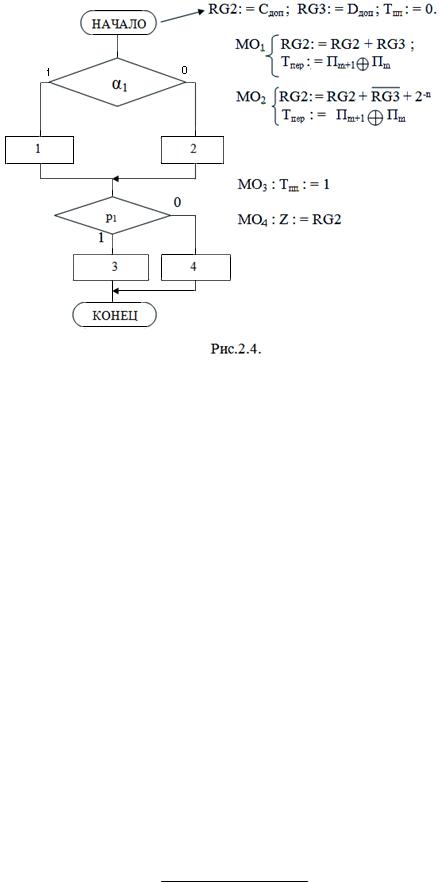
18
Способ 1б. (Сложение-вычитание в модифицированном дополнительном коде чисел, поступающих в дополнительном коде; результат выдается в дополнительном коде.)
Модификация кода заключается в использовании двух знаковых разрядов,
в которых 00 означает «плюс», 11 – «минус», 01 – положительное ПРС, 10
– отрицательное ПРС. При несовпадении двух знаковых разрядов резуль-
тата формируется сигнал обнаружения ПРС.
Отличия в ОС (по сравнению со способом 1а):
1)RG2 и KSM снабжаются еще одним знаковым разрядом с номером
(m+1).
2)p1 = RG2(m+1) 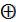 RG2(m)
RG2(m)
Отличия в графе МП:
1)Значения С и D подаются в KSM с двумя знаковыми разрядами, при-
чем 2-й знаковый разряд в RG3 экономится за счет дублирования знака
D на входах KSM. Соответственно меняется запись МО1, МО2, и МО4:
МО1: RG2: = RG2 + RG3(m).RG3(m:0)
МО2: RG2:=RG2 + RG3(m).RG3(m:0) +2-n
МО4: Z : = RG2(m:0)
2)В начале операции выполняется МО: RG2 : = Cмод.доп
19
В остальном граф МП и ОС такие же, как в способе 1а.
Пример: m=3, n=0, F=C–D, C= –7, D= +6.
Сдоп = 1 001 |
Смод.доп = 11 001 |
|
Dдоп =0 110 |
+ |
|
|
(–D)мод.доп = 11 001 |
|
|
|
1 |
|
10 011 |
|
ПРС Способ 2а. (Сложение-вычитание в дополнительном коде чисел, посту-
Способ 2а. (Сложение-вычитание в дополнительном коде чисел, посту-
пающих в прямом коде; F формируется в прямом коде).
Правила.
1) Если F=C+D, то выполняются 3 этапа.
1-й этап. Получение Сдоп , если С < 0
2-й этап. Fдоп = (Сдоп + Dдоп)(mod2m+1), т.е.:
если D>0, то выполняется МО: RG2: = RG2+0.RG3(m–1:0);
если D<0, то выполняется МО: RG2: = RG2+1.RG3(m–1:0) + 2-n; 3-й этап. Перевод Fдоп в прямой код, если F < 0
2)Если F=C–D, то F=C+(–D), т.е. вычитание сводится к сложению путем предварительного инвертирования знака D.
Как и в способе 1а, здесь сигнал ПРС формируется при Пm+1  Пm = 1,
Пm = 1,
а также при получении результата Fдоп = (–2m)доп . Дело в том, что (–2m)пр переполняет разрядную сетку.
Пример: m=3, n=0, F=C+D, С= –3, D= –5, Cпр=1011, Dпр=1101
1-й этап: Cдоп=1101;
2-й этап: Fдоп=1101
+1010
1
1000 = Fдоп=(– 8)доп=(–2m)доп 3-й этап: Fпр= 1111
+1
0000 = Fпр = + 0 [вместо (–8)]
Результат не верен, т.к. (–8)пр= 1 1000 при m=3 вызывает ПРС. m=4
В отличие от способа 1а, в ОС (рис.2.5) добавляются 3 сигнала состояния:
p2= RG2(m)=знак С, p3= RG3(m)= знак D, p4=[RG2(m–1:0)=0].

20
Сигнал ПРС формируется, если p1= Пm+1  Пm=1, или получен резуль-
Пm=1, или получен резуль-
тат Fдоп= (–2m)доп, т.е., p2p4 = 1.
p1
Tпер
М2
П m 1
П m
|
|
|
m |
1 |
p4 |
|
|
|
Z(m:0) |
|
|
p2 |
|
|
|
|
|
зн |
|
RG2 |
|
|
|
m |
m-1 |
0 |
|
|
|
|
|
|
m |
KSM |
0 |
|
p3
зн |
RG3 |
|
|
m m-1 |
0 |
||
|
Рис. 2.5
Исходя из приведенных правил, получаем следующий список МО, поря-
док выполнения которых определяется графом МП на рис. 2.6.
МО1: RG3(m): = RG3(m) (Изменение знака D на противоположный)
МО2: RG2(m-1:0): = RG2(m–1:0) ;
МО3: RG2: = RG2+2-n ;
МО4: RG2: = RG2+ 0.RG3(m–1:0)
Тпер: = Пm+1 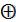 Пm
Пm
МО5 RG2: = RG2+ 1. RG3(m–1:0)+2-n ;
Тпер: = Пm+1  Пm
Пm
МО6: Tпп:= 1; МО7: Z : = RG2 ;
