Zusammenfassung

Die modulare Entwurfsmethode ist ein strukturiertes Vorgehen für den Entwurf von Systemen. Die Idee dabei ist es, zuerst einfache Systeme, sogenannte Module, zu bauen und anschließend diese auf ihre Korrektheit zu prüfen. Danach benutzt man die Module als Bausteine für komplexere Systeme. Dieser Vorgang kann beliebig oft wiederholt werden, bis man sehr komplexe Systeme erzeugt hat.

Für zwei endlichen Automaten kann man einen einzigen endlichen Automaten entwerfen, der die kompletten Informationen über beide besitzt. So kann man systematisch immer komplexere Automaten bauen, insbesondere wenn die zu akzeptierende Sprache durch mehrere Bedingungen beschrieben wird. Dann baut man zuerst für jede einzelne Bedingung einen endlichen Automaten und setzt diese danach zu einem komplexeren endlichen Automaten zusammen.

Kontrollfragen

1.Warum ist eine Überprüfung der Korrektheit von entworfenen technischen Systemen wichtig? Inwiefern vereinfacht ein systematischer Entwurf die Verifikation?

2.Wie unterschiedlich kann man den Begriff der Simulation auslegen? Um welchen geht es bei der Simulation zweier endlicher Automaten durch einen endlichen Automaten?

3.Was bedeutet „Modularität“ im Zusammenhang mit dem Entwurf von technischen Systemen?

4.Für welche Arten von Problemspezifikationen (Beschreibungen der zu akzeptierenden Sprache) würdest du die modulare Entwurfsmethode vorziehen? Warum?

Kontrollaufgaben

1.Entwirf jeweils einen endlichen Automaten mit der Entwurfsmethode der Zustandsklassen.

a)L1 = {111x1 | x {0, 1} }

b)L2 = {xyz | y {00, 11} und x, z {0, 1} }

c)L3 = {u {0, 1} | |u|1 = 1 oder |u|1 > 2}

487

d)L4 = {u {0, 1} | |u|0 mod 3 = |u|1 mod 3}

2.Verwende die modulare Entwurfsmethode, um jeweils einen endlichen Automaten für folgende Sprachen zu konstruieren. Die Sprachen L1, L2, L3 und L4 sind dieselben wie in der Kontrollaufgabe 1.

a)L1 ∩L2

b)L1 L2

c)L3 −L2

d)({0, 1} −L1) L4

e)({0, 1} −L2) ∩L3

f)L3 −({0, 1} −L1)

g)L1 ∩L3 ∩L4

h)(L1 L3) L4

i)L1 ∩(L3 L4)

j)L2 −(L1 L4)

Lösungen zu ausgesuchten Aufgaben

Aufgabe 6.1(a)

Wenn der endliche Automat in Abb. 6.4 die Sprache L(M1) −L(M2) akzeptieren soll, müssen wir solche Zustände (r, s) als akzeptierende Zustände wählen, für die r ein akzeptierender Zustand von M1 und s kein akzeptierender Zustand von M2 ist. In unserem Beispiel (Abb. 6.2 und Abb. 6.3) sind es die Zustände

(q0, p1) und (q0, p2).

Aufgabe 6.1(c)

Wenn der endliche Automat in Abb. 6.4 die Sprache {0, 1} − (L(M1) ∩ L(M2)) akzeptieren soll, müssen seine akzeptierenden Zustände alle Paare (r, s) sein, für die nicht gleichzeitig gilt, dass beide r und s akzeptierende Zustände des jeweiligen Automaten M1 und M2 (Abb. 6.2 und Abb. 6.3) sind. Damit erhalten wir die folgende Liste von akzeptierenden Zuständen:

Also sind es alle Zustände außer (q0, p0) und (q0, p3), die die Menge aller akzeptierenden Zustände für die Erkennung der Sprache (L(M1) ∩L(M2) bilden.

Aufgabe 6.2(g)

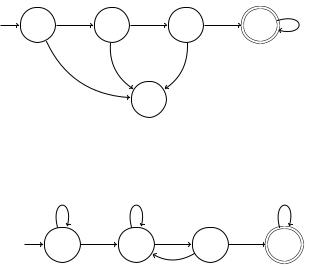
Wir entwerfen den gesuchten endlichen Automaten, indem wir zuerst die endlichen Automaten für die Sprachen L1 = {011y | y {0, 1} } und L2 = {u100v | u, v {0, 1} } bilden. Diese Automaten sind in Abb. 6.5 und Abb. 6.6 dargestellt.

Abbildung 6.6

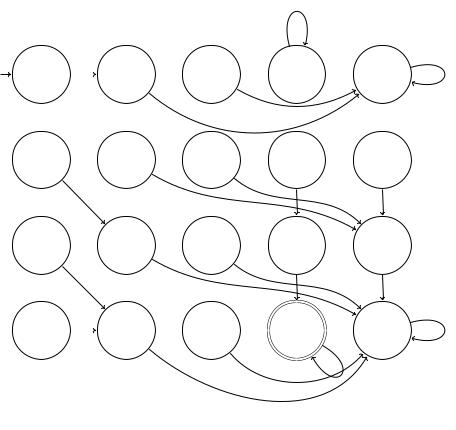
Unsere Aufgabe ist es, den endlichen Automaten für die Sprache L1 ∩L2 zu konstruieren. Der einzige akzeptierende Zustand ist (q3, p3). Die 0-Kanten des entsprechenden Automaten sind in Abb. 6.7 gezeichnet. Die 1-Kanten aus jedem Zustand zu bestimmen, überlassen wir gerne dir.

489

Abbildung 6.7

Lektion 7

Größe endlicher Automaten und

Nichtexistenzbeweise

Hinweis für die Lehrperson Diese Lektion ist nur Klassen mit dem Schwerpunkt in der Mathematik oder einzelnen Schülerinnen und Schülern mit ausgeprägtem Interesse an der Mathematik gewidmet. Wenn man entsprechend langsam und vorsichtig vorgeht, ist der erste Teil bis zu Beispiel 7.2 auch in sprachlich orientierten Klassen noch zu bewältigen.

Es ist in der Wissenschaft leichter, die Existenz eines Objekts mit gewissen Eigenschaften1 zu beweisen als seine Nichtexistenz2. Die Existenz belegt man, indem man das Objekt einfach konstruiert und somit im wahrsten Sinne des Wortes konstruktiv vorgeht. Die Nichtexistenz eines Objekts zu belegen erfordert den Nachweis, dass jeder Herstellungsversuch scheitern wird. Aber was bedeutet jeder Versuch? Das sind nicht nur die Wege, die uns eingefallen sind, sondern auch solche, die uns nie einfallen werden. Wie kann man wissen, dass auch unbekannte Konzepte nicht helfen werden, wenn man noch nichts von ihnen ahnt? Und dieser Gedanke ist gerade das, was den Beweis der Nichtexistenz erschwert. Die Beweise des Unmöglichen führen jedoch zu den wichtigsten Errungenschaften der Wissenschaft. Sie erforschen die Grenze zwischen dem, was möglich und was nicht möglich ist, und liefern so wichtige Naturgesetze.

Diese Lektion vermittelt, wie man die Nichtexistenz von kleinen endlichen Automaten oder sogar die Nichtexistenz von endlichen Automaten für eine gegebene Sprache formal begründet. Weil endliche Automaten eine Klasse von sehr einfachen3 Algorithmen bil-

1oder die Möglichkeit eines Ereignisses

2Unmöglichkeit eines Ereignisses

3stark eingeschränkten

J. Hromkoviˇc, Lehrbuch Informatik, DOI 10.1007/978-3-8348-9692-6_28, © Vieweg+Teubner |GWV Fachverlage GmbH, Wiesbaden 2008

den, sind die Nichtexistenzbeweise für endliche Automaten relativ leicht durchführbar. Trotzdem lernt man dabei zu verstehen, wie man solche Argumentationen führt.

Wir beginnen mit einer einfachen Aufgabe. Für eine gegebene Sprache L und eine gegebene positive ganze Zahl m soll gezeigt werden, dass jeder EA für L mindestens m Zustände benötigt. Wir demonstrieren es an einem Beispiel.

Beispiel 7.1 Betrachte die Sprache

L = {x {0, 1} | |x|0 mod 4 = 3}.

Unsere Aufgabe ist zu zeigen, dass jeder EA, der L akzeptiert, mindestens vier Zustände hat. Man könnte einen EA M mit L(M) = L und vier Zuständen jetzt konstruieren und dann argumentieren, man könne es nicht anders machen. Dies ist aber gerade eine unzulässige Argumentation, weil wir nie wissen, ob es nicht auch andere Ideen zur Konstruktion eines EA für M gibt. Jetzt könnte man eine allgemeine Argumentation vermeiden, indem man alle möglichen endlichen Automaten mit höchstens drei Zuständen konstruiert und dann für jeden dieser EA A zeigt, dass L(A) =L gilt. Diesen aufwendigen Weg wollen wir aber nicht beschreiten. Wir wollen stattdessen einige Eigenschaften von L und von endlichen Automaten finden, welche die Existenz eines EA mit weniger als vier Zuständen für L ausschließen. Dabei hilft uns die Behauptung aus Lektion 3:

„Wenn ein EA M die Berechnung auf zwei Wörtern x und y in dem gleichen Zustand beendet (wenn x und y in die gleichen Zustandsklassen gehören,

d. h. wenn (q0, x) M (p, λ ) und (q0, y) M (p, λ ) für einen Zustand p), dann enden für alle Wörter z die Berechnungen von M auf xz und yz in dem

gleichen Zustand und somit gilt

xz L(M) yz L(M).“

Mit anderen Worten, wenn ein EA M nach dem Lesen von zwei unterschiedlichen Eingabepräfixen x und y denselben Zustand erreicht, kann er nicht mehr zwischen x und y unterscheiden und der Rest der Berechnung hängt nur von dem noch nicht gelesenen Suffix z ab.

Wenn man zeigen möchte, dass mindestens vier Zustände benötigt werden, um L zu akzeptieren, reicht es aus, vier Wörter x1, x2, x3 und x4 zu finden, von denen keine zwei zur selben Zustandsklasse gehören. Intuitiv sind wir der Meinung, jeder EA für L muss

493

die Anzahl der gelesenen Nullen modulo 4 zählen. Deswegen wählen wir

x1 = λ x2 = 0 x3 = 00

x4 = 000.

Jetzt müssen wir für alle i, j {1, 2, 3, 4}, i < j, ein Wort zi j finden, so dass

genau eines der Wörter xizi j und x j zi j in L liegt.

Fangen wir mit x1 = λ und x2 = 0 an. Wenn wir

z12 = 00

nehmen, dann gilt

x1z12 = 00 / L und x2z12 = 000 L.

Somit gehören x1 und x2 zu unterschiedlichen Zustandsklassen. Jetzt wählen wir

z13 = 000

Dann gilt

x1z13 = 000 L und x3z13 = 00000 / L

und somit gehören x1 und x3 zu unterschiedlichen Zustandsklassen. Weiter wählen wir

z14 = λ

und somit gilt

x1z14 = λ / L und x4z14 = 000 L.

Für x2 und x3 suchen wir

z23 = 00000

aus. Somit gilt

x2z23 = 000000 / L und x3z23 = 0000000 L.

Für x2 und x4 können wir

z24 als 00

wählen und somit gilt

x2z24 = 000 L und x4z24 = 00000 / L.

Für das letzte Paar (x3, x4) können wir

z34 = λ

nehmen und erhalten

x3z34 = 00 / L und x4z34 = 000 L.

Weil kein Paar der vier Wörter x1, x2, x3 und x4 zur gleichen Zustandsklasse gehören darf, muss man mindestens vier unterschiedliche Zustandsklassen haben. Somit hat jeder

b)Bestimme für jedes Paar (xi, x j ), i, j {1, 2, 3, 4} und i < j eine unendliche Menge Zi j von Wörtern, so dass für alle y Zi j gilt

xiy L und x j y / L.

Aufgabe 7.2 Wähle im Beispiel 7.1 andere Wörter für x1, x2, x3 und x4 aus und führe die Argumentation mit den Wörtern deiner Wahl durch.

Aufgabe 7.3 Bestimme, welche der folgenden Wortmengen x1, x2, x3, x4 zu einem erfolgreichen Beweis des Beispiels 7.1 führen und welche nicht. Begründe deine Behauptung.

495

Aufgabe 7.4 Beweise, dass man für jede der folgenden Sprachen mindestens vier Zustände braucht, um sie zu akzeptieren.

a){x101y | x, y {0, 1} },

b){x {0, 1} | |x|0 ist gerade und |x|1 ist ungerade},

c){x110 | x {0, 1} },

d){111},

e){1x00 | x {0, 1} },

f){0, 1}2,

g){x {a, b} | |x| = 1 oder |x| > 2}.

Aufgabe 7.5 Wie viele Zustände braucht man mindestens, um folgende Sprachen zu akzeptieren?

a){x1y | x {0, 1} , y {0, 1}2},

b){x0101y | x, y {0, 1} },

c){x {0, 1, 2} | |x|0 mod 3 = 2 und x = u22v für u, v {0, 1, 2} },

d){x {0, 1} | x = uv, wobei u {0, 1} und v {00, 01}}.

Begründe deine Behauptung.

Aufgabe 7.6 * (Knobelaufgabe)

a) Sei

Lk = {x1y | x {0, 1} , y {0, 1}k−1}

= {w {0, 1} | das k-te Bit, vom Ende aus gezählt, in w ist 1}.

Beweise für alle k N −{0}, dass jeder endliche Automat, der L akzeptiert, mindestens 2k −1 Zustände braucht.

b)Sei Mn = {wcw | w {a, b}n} {a, b, c} eine endliche Sprache für ein n N. Beweise für alle n N −{0}, dass jeder EA für Mn mindestens 2n Zustände haben muss.

Hinweis für die Klasse Der Rest dieser Lektion ist nicht obligatorisch. Es wird empfohlen, nur dann weiterzulesen, wenn man dieses Thema als spannende Herausforderung empfindet.

Wir haben gelernt, untere Schranken für die Größe von endlichen Automaten zu beweisen. Jetzt wollen wir diese Technik erweitern, um die Nichtexistenz von endlichen Automaten für konkrete Sprachen zu beweisen. Welche Sprachen sollten für endliche Automaten schwierig sein? Einfach diejenigen mit einer unbeschränkten4 Anzahl der zu beobachtenden Merkmale.

Beispiel 7.2 Betrachte die Sprache

L = {0n1n | n N}.

Intuitiv sehen wir den Bedarf, beim Lesen von links nach rechts zuerst die Nullen zu zählen und ihre Anzahl zu speichern, denn so kann man später die Anzahl Nullen mit der Anzahl von Einsen zu vergleichen. Formal ausgedrückt betrachten wir die unendliche Folge von Wörtern

x1 = 0, x2 = 02, x3 = 03, . . . , xi = 0i, . . .

Wir müssen zeigen, dass keine zwei dieser Wörter zur selben Zustandsklasse eines EA M gehören können, vorausgesetzt M würde L akzeptieren. Seien xi = 0i und x j = 0 j zwei beliebige Wörter aus dieser Folge für i =j. Dann wählen wir

zi j = 1i.

Offensichtlich gilt

xizi j = 0i1i L und x j zi j = 0 j 1i / L.

Also muss man nach dem Lesen von 0i und 0 j mit i =j unbedingt in zwei unterschiedliche Zustände übergehen. Damit muss der Automat mindestens so viele Zustände haben, wie es Wörter in der unendlicher Folge x1, x2, x3, . . . gibt. Kein endlicher Automat hat aber unendlich viele Zustände und deshalb kann L von keinem endlichen Automaten erkannt werden.

Aufgabe 7.7 Was wäre passiert, wenn wir in Beispiel 7.2 xi = 02i gewählt hätten? Könnte man dann den Beweis der Nichtexistenz auch erfolgreich zu Ende bringen? Schlage einige andere Möglichkeiten für ein xi vor. Gibt es auch eine Variante, bei der jedes xi mindestens eine Eins enthält?

4Unbeschränkt bedeutet in diesem Zusammenhang, die Anzahl der zu speichernden Charakteristiken kann mit der Eingabelänge wachsen und ist somit unendlich.

497

Aufgabe 7.8 Beweise, dass die Sprache L = {0n12n | n N} keine reguläre Sprache ist.

Hinweis für die Lehrperson Die Schwierigkeit des vorgeführten Nichtexistenzbeweises liegt darin, gleichzeitig unendlich viele Wörter zu betrachten und davon unendlich viele Paare zu bilden. Dann wird allgemein ein zi j zu einem beliebigen Paar (xi, x j ) bestimmt. Indirekte Beweise ermöglichen uns, das Unendliche aus der Beweisführung zu verbannen. Damit ist aber die Bearbeitung der Lektion über Beweise aus dem Modul „Geschichte und Begriffsbildung“ eine notwendige Voraussetzung für das Erwerben der Methode, die wir in Beispiel 7.3 präsentieren.

Wenn man ungern mit unendlichen Wortfolgen argumentiert, kann man dies umgehen, indem man indirekte Beweise führt. Hier setzt man zuerst das Gegenteil von dem voraus, was man beweisen will, und zeigt dann, dass es zum Widerspruch führt. Wie man es konkret realisiert, zeigt das folgende Beispiel.

Beispiel 7.3 Wir sollen beweisen, dass

L = {anb2nc3n | n N}

nicht durch endliche Automaten akzeptiert werden kann. Man nutzt das Schema des indirekten Beweises (siehe Module „Logik“ und „Geschichte und Begriffsbildung“) und setzt das Gegenteil davon voraus. Das heißt also, wir nehmen die Existenz eines endlichen Automaten M mit L(M) = L an. Weil M endlich ist, ist seine Zustandsmenge Q auch endlich. Sei |Q| = k für eine positive ganze Zahl k. Jetzt zeigen wir, dass M die Sprache L nicht akzeptiert und man dadurch einen Widerspruch unserer Annahme erhält. Wir wählen die Wörter

x1 = a1b2, x2 = a2b4, . . . , xi = aib2i, . . . , xk+1 = ak+1b2(k+1)

und wollen belegen, dass keine zwei von diesen k + 1 Wörtern zur selben Zustandsklasse gehören dürfen. Im Prinzip gibt es aber nur k Zustände für M. Also müssen i, j {1, . . . , k}, i < j, existieren, so dass xi und x j zu einer gleichen Zustandsmenge von M gehören. Dann wählen wir

zi j = c3i.

Offensichtlich gilt

xizi j = aib2ic3i L und x j zi j = a j b2 j c3i / L.

Somit kann M die Sprache L nicht akzeptieren, weil M entweder beide Wörter xizi j und x j zi j akzeptieren oder beide verwerfen muss. Wir haben also den gewünschten Widerspruch belegt. Damit gilt unsere Annahme nicht, was bedeutet, dass das Gegenteil der Annahme gilt. Das Gegenteil unserer Annahme ist:

Aufgabe 7.9 Wähle andere k + 1 Wörter x1, x2, ..., xk+1 für Beispiel 7.3 und führe den indirekten Beweis mit den von dir ausgesuchten Wörtern.

Aufgabe 7.10 Führe einen indirekten Beweis, dass die Sprache {0n1n | n N} aus Beispiel 7.3 von keinem endlichen Automaten akzeptiert werden kann.

Aufgabe 7.11 Führe einen direkten Nichtexistenzbeweis eines EA für die Sprache {anb2nc3n | n N} nach dem Beweismuster aus Beispiel 7.3.

Den indirekten Beweis aus Beispiel 7.3 kann man auch vermeiden. Man beweist, dass es für jedes k N keinen endlichen Automaten mit k Zuständen für L gibt. Dann reicht es, für jedes k eine gute Auswahl von k + 1 Worten zu treffen, damit keine zwei dieser Wörter in die gleiche Zustandsklasse gehören.

Aufgabe 7.12 Stelle für die folgenden Sprachen jeweils direkte und indirekte Beweise der Nichtexistenz von endlichen Automaten her.

a){0n12n | n N},

b){w#w | w {0, 1} } über {0, 1, #},

c){w#v | w, v {0, 1} , w =v} über {0, 1, #},

d){0n1n2 | n N} über {0, 1},

e){w {0, 1} | |w|0 = 2|w|1},

f){w {a, b, c} | |w|a + |w|b = |w|c.

Aufgabe 7.13 (Knobelaufgabe)

Bestimme, ob folgende Sprachen durch endliche Automaten akzeptiert werden können. Begründe