
- •Vorwort
- •Inhaltsverzeichnis
- •Einleitung
- •Programmieren in LOGO
- •Warum unterrichten wir Programmieren?
- •Unser Programmiervorkurs in LOGO, oder Programmieren in 10 Minuten
- •Die Programmierumgebung in LOGO
- •Zusammenfassung
- •Kontrollfragen
- •Kontrollaufgaben
- •Lösungen zu ausgesuchten Aufgaben
- •Kontrollfragen
- •Kontrollaufgaben
- •Lösungen zu ausgesuchten Aufgaben
- •Zusammenfassung
- •Kontrollfragen
- •Kontrollaufgaben
- •Lösungen zu ausgesuchten Aufgaben
- •Zusammenfassung
- •Kontrollfragen
- •Kontrollaufgaben
- •Lösungen zu ausgesuchten Aufgaben
- •Zusammenfassung
- •Kontrollfragen
- •Kontrollaufgaben
- •Lösungen zu ausgesuchten Aufgaben
- •Zusammenfassung
- •Kontrollfragen
- •Kontrollaufgaben
- •Lösungen zu ausgesuchten Aufgaben
- •Zusammenfassung
- •Kontrollfragen
- •Kontrollaufgaben
- •Lösungen zu ausgesuchten Aufgaben
- •Zusammenfassung
- •Kontrollfragen
- •Kontrollaufgaben
- •Lösungen zu ausgesuchten Aufgaben
- •Zusammenfassung
- •Kontrollfragen
- •Kontrollaufgaben
- •Lösungen zu ausgesuchten Aufgaben
- •Zusammenfassung
- •Kontrollfragen
- •Kontrollaufgaben
- •Lösungen zu ausgesuchten Aufgaben
- •Zusammenfassung
- •Kontrollfragen
- •Kontrollaufgaben
- •Lösungen zu ausgesuchten Aufgaben
- •Zusammenfassung
- •Kontrollfragen
- •Kontrollaufgaben
- •Lösungen zu ausgesuchten Aufgaben
- •Zusammenfassung
- •Kontrollfragen
- •Kontrollaufgaben
- •Lösungen zu ausgesuchten Aufgaben
- •Zusammenfassung
- •Kontrollfragen
- •Kontrollaufgaben
- •Lösungen zu ausgesuchten Aufgaben
- •Vorwort und Zielsetzungen
- •Zusammenfassung
- •Kontrollfragen
- •Zusammenfassung
- •Kontrollfragen
- •Kontrollaufgaben
- •Lösungen zu ausgesuchten Aufgaben
- •Zusammenfassung
- •Kontrollfragen
- •Zusammenfassung
- •Kontrollfragen
- •Zusammenfassung
- •Kontrollfragen
- •Kontrollaufgaben
- •Lösungen zu ausgesuchten Aufgaben
- •Zusammenfassung
- •Kontrollfragen
- •Kontrollaufgaben
- •Lösungen zu ausgesuchten Aufgaben
- •Zielsetzung
- •Zusammenfassung
- •Kontrollfragen
- •Kontrollaufgaben
- •Lösungen zu ausgesuchten Aufgaben
- •Zusammenfassung
- •Kontrollfragen
- •Kontrollaufgaben
- •Lösungen zu ausgesuchten Aufgaben
- •Zusammenfassung
- •Kontrollfragen
- •Kontrollaufgaben
- •Lösungen zu ausgesuchten Aufgaben
- •Gerechtigkeit
- •Freiheitsgrade
- •Zusammenfassung
- •Kontrollfragen
- •Kontrollaufgaben
- •Lösungen zu ausgesuchten Aufgaben
- •Zusammenfassung
- •Kontrollfragen
- •Kontrollaufgaben
- •Lösungen zu ausgesuchten Aufgaben
- •Zusammenfassung
- •Kontrollfragen
- •Kontrollaufgaben
- •Lösungen zu ausgesuchten Aufgaben
- •Sachverzeichnis

247
Zusammenfassung
Die Methoden zur Lösung unterschiedlicher Aufgabentypen lernt man besonders gut verstehen, wenn man sie in Programme umsetzt. Mit Hilfe der trigonometrischen Funktionen kann man in der Welt der Dreiecke aus gegebenen Informationen weitere Informationen ableiten oder sogar alles über das untersuchte Objekt erfahren.
Bei der Entwicklung von Programmen ist es wichtig zu beobachten, dass es nicht nur um das eigene Programmieren geht. Zuerst muss man das mathematische Denken anwenden, um das Problem zu analysieren und Zusammenhänge festzustellen. Erst wenn der Lösungsweg vollständig verstanden wurde, kann man mit dem Programmieren beginnen. Das muss aber nicht bedeuten, dass das Programmieren selbst nur eine lästige Routinearbeit ist. Manchmal braucht man neue Ideen, wie bei der Berechnung von arcsin, um mit den vorhandenen, beschränkten Mitteln einer Programmiersprache die mathematisch beschriebenen Lösungswege umzusetzen.
Kontrollfragen
1.Warum hat man die trigonometrischen Funktionen eingeführt? Was haben die Strahlensätze damit zu tun?
2.Aus welchen Daten über ein rechtwinkliges Dreieck kannst du alle anderen Seitenund Winkelgrößen bestimmen?
3.Sei f eine wachsende Funktion, die durch ein Programm berechnet werden kann. Wie kann man mit Hilfe der while-Schleife für den gegebenen Wert f (x) eine Annäherung des Wertes x berechnen? Wie kann man es mit beliebiger Genauigkeit machen?
4.Sei f eine Funktion, die man für jedes Argunment mit einem Programm berechnen kann. Sei [a,b] ein Intervall, in dem f genau ein Extremum hat. Wie kann man mit der Hilfe einer While-Schleife für einen frei wählbaren Wert des Parameters :APP ein i finden, sodass die Extremstelle im Intervall [i·APP,(i + 1)·APP] liegt?
Kontrollaufgaben
1.Schreibe ein Programm, das für die drei gegebenen Werte |SA1|, |SA2| und |SA3| das Bild aus Abb. 13.1 auf Seite 240 zeichnet. Im Unterschied zu Aufgabe 13.1 müssen die Strecken A1B1, A2B2 und A3B3 als Strecken und nicht als Geraden gezeichnet werden.
248 |
Lektion 13 Integrierter LOGOund Mathematikunterricht: Trigonometrie |
2.Entwickle ein Programm, das für gegebene Werte β und c eines rechtwinkligen Dreiecks alle anderen Seitenund Winkelgrößen berechnet und das Dreieck zeichnet.
3.Entwirf ein eigenes Programm ARCTANGENS zur Berechnung von arctan(x) für ein beliebiges positives Argument x.
4.Entwirf ein Programm, das für eine gegebene natürliche Zahl n ≥ 3 und einen gegebenen Kreisradius r die Fläche des den Kreis umschreibenden, regelmäßigen n-Ecks berechnet.
5.Entwickle ein Programm, das für eine gegebene positive Zahl n die n Dezimalstellen von π hinter dem Komma berechnet.
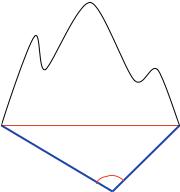
6.Man möchte die Länge eines Tunnels berechnen, der unter einem Berg hindurch führt. Die einzigen Daten, die man kennt, sind die Entfernungen a und b und der Winkel γ aus Abb. 13.6. Schreibe ein Programm, das für die gegebenen Werte von a, b und γ die Länge des Tunnels berechnet.
Tunnel
A B
a
bγ
C
Abbildung 13.6
7.Entwickle ein Programm, das für die folgenden Funktionen und Intervalle [a,b] ihrer Argumente ein lokales Maximum näherungsweise findet. Die Genauigkeit der Näherung soll durch den Parameter :APP des Programms gegeben werden. Das Programm soll einen Wert :X ausgeben, so dass es ein lokales Maximum gibt, dessen Wert höchstens um :APP von :X abweicht.
a)f (α ) = sin(α ) ·cos(α ) für α [0, 90]
b)f (x) = (20 −x) ·(20 + x) für x [−10, 10]

249
c) f (x) = ax3 + bx2 + cx + d für x [0, 100], wobei a, b, c, d beliebige Werte sind, die man als Eingaben des Programms betrachtet.
Lösungen zu ausgesuchten Aufgaben
Aufgabe 13.4
Wir kennen die Fläche F des Dreiecks ABC aus Abb. 13.7 und die Winkelgröße von α .
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
α |
|
|
|
|
|
|
|
|
|
|
|
c |
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
β |
|
• |
|
||
|
|
|
|
|
|
B |
a |
C |
||||
|
|
|
|
|
|
|
|
Abbildung 13.7 |
|
|
||
Wir wissen, dass |
|
|
|
|
|
|
|
|
||||
F = |
a ·b |
|
und |
|
tan α = |
a |
|
|
|
|
||
|
|
|
b |
|
|
|
||||||
2 |
|
|
|
|
|
|
|
|||||
gilt. Aus der ersten Gleichung erhalten wir |
|
|
|
|||||||||
b = |
2F |
. |
|
|
|
|
|
|
(13.1) |
|||
|
|
|
|
|
|
|
||||||
|
|
a |
|
|
|
|
|
|
|
|
||
Wenn wir den Ausdruck für b in die zweite Gleichung tan α = ab einsetzen, erhalten wir
tan α = |
a2 |
|
2F |
|
|
|
|
|
und somit |
|
|
√ |
·F ·tan α |
(13.2) |
a = 2 |
Wenn wir a kennen, können wir es in (13.1) einsetzen, um b zu bestimmen. Die Seitengröße von c erhalten wir durch die Verwendung des Satzes von Pythagoras oder mittels
a c = sin α
Damit können wir das Programm wie folgt schreiben:

250 Lektion 13 Integrierter LOGOund Mathematikunterricht: Trigonometrie
to DRFLA :F :ALPHA
make "a sqrt(2 :F tan(:ALPHA) make "b 2 :F/:a
make "c :a/sin(:ALPHA) rt 90 fd :b lt 180-:ALPHA fd :c rt 270−:ALPHA
fd :a rt 180 end
Aufgabe 13.8
Die Entfernung s des Beobachters von der Oberfläche des Planeten B (s. Abb. 13.3 auf Seite 244) kann man einfach durch das physikalsiche Gesetz
Strecke = Geschwindigkeit ·Zeit
bestimmen. Weil der Strahl die Strecke s in der Zeit x zweimal durchläuft, erhalten wir
2s = 300 000 ·x
und somit
s = 150 000 ·x.
In Abb. 13.3 auf Seite 244 betrachten wir für die Bestimmung des Radius vom Planeten B die Strecke CD statt der Tangente. Bei großen Entfernungen ist der Unterschied vernachlässigbar. Im Dreieck zwischen D, C und dem Mittelpunkt des Planeten B gilt
sin |
α |
= |
r |
|
|
|
|
|
|
|
|·(r + s) |
|
|
|
|
|
|
|
|
|
|
|
|
||||
2 |
r + s |
|
|
|
|
|
α |
|
|||||
(r + s) ·sin |
α |
= r |
|
|
|
|
|
|
|
|−r ·sin |
|
||
2 |
|
|
|
|
|
α |
2 |
||||||
s ·sin |
α |
= 1 −sin |
|
·r |
|
|
|||||||
2 |
2 |
|
|
||||||||||
|
|
r = |
· |
|
|
α |
|
|
|
||||
|
|
|
s |
sin |
|
α |
|
|
|
|
|
||
|
|
|
|
2 |
|
|
|
|
|
||||
|
|
|
1 −sin |
|
2 |
|
|
|
|
|
|||
Jetzt kann man aus den entwickelten Formeln das Programm aufschreiben.
to PLANET :X :ALPHA make "s 150000 :X pr:s
make "d sin(:ALPHA/2) make "r (:s :d)/(1-:d) pr :r
end
Lektion 14
Integrierter LOGOund Mathematikunterricht: Vektorgeometrie
Die Programmiersprache LOGO kann uns helfen, Programme für Lösungen von vielen grundlegenden Aufgabenstellungen im zweidimensionalen Raum zu entwickeln und die Konstruktionen mit Hilfe der Schildkröte zu zeichnen. Wenn wir es schaffen, Aufgabenstellungen auf diese Art und Weise zu lösen, können wir sicher sein, dass wir die Lösungsmethode gut beherrschen, weil wir sie sogar einer Maschine ohne Intellekt beibringen können.
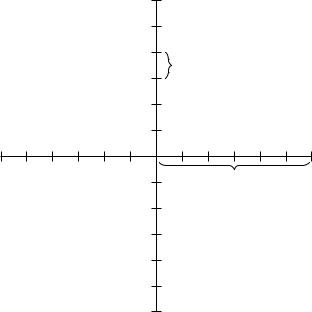
Wir fangen damit an, dass wir ein Programm zur Erzeugung von Koordinatensystemen schreiben. Die Einheiten sollen in Schritten frei wählbar sein, um mit beliebigen Zahlen graphisch umgehen zu können (siehe Abb. 14.1). Wie üblich gehen wir modular vor.
to ACHSE :AN :EINHEIT
repeat :AN [ fd :EINHEIT rt 90 fd 5 bk 10 fd 5 lt 90]
bk :AN :EINHEIT rt 180
repeat :AN [ fd :EINHEIT rt 90 fd 5 bk 10 fd 5 lt 90]
bk :AN :EINHEIT rt 180
end
J. Hromkoviˇc, Lehrbuch Informatik, DOI 10.1007/978-3-8348-9692-6_15, © Vieweg+Teubner |GWV Fachverlage GmbH, Wiesbaden 2008
252 |
Lektion 14 Integrierter LOGOund Mathematikunterricht: Vektorgeometrie |
:EINHEIT
:AN – Anzahl der Einheiten
Abbildung 14.1
to KOOR :AN :EINHEIT
ACHSE :AN :EINHEIT
rt 90
ACHSE :AN :EINHEIT
lt 90
end
Aufgabe 14.1 Modifiziere das Programm KOOR so, dass man auf den verschiedenen Achsen sowohl die Anzahl, als auch die Schrittgröße der Einheiten wählen kann.
Punkte können wir in diesem Koordinatensystem durch kleine Kreise zeichnen:
to PUNKT :EINHEIT :X :Y KOOR 240/:EINHEIT :EINHEIT
pu fd :Y :EINHEIT rt 90 fd :X :EINHEIT pd KREISE 1/36
end
253
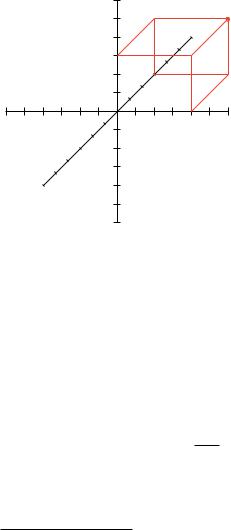
Abbildung 14.2 Punkt (4, 3, 3) in einem dreidimensionalen Koordinatensystem
Aufgabe 14.2 Entwickle ein Programm zum Zeichnen eines Punktes in einem dreidimensionalen Raum (Abb. 14.2). Die Z-Achse soll unter dem Winkel von 45◦ mit 23 der Größe der Einheiten auf der X - und Y -Achse dargestellt werden. Der Punkt mit den Koordinaten (X ,Y, Z) soll als die hintere, rechte Ecke eines Würfels eingezeichnet werden.
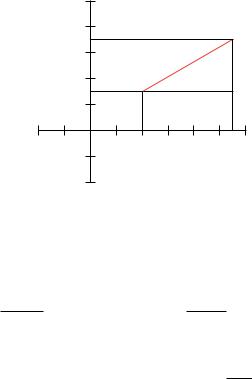
Beispiel 14.1 Eine der grundlegenden Aufgaben in der Geometrie ist es, die Strecke zwischen zwei gegebenen Punkte P1 = (X1,Y1) und P2 = (X2,Y2) zu zeichnen. Wir werden im Weiteren Koordinatensysteme schwarz, Strecken rot und Geraden blau zeichnen. Die Punkte können wir schon einzeichnen. Um die Strecke P1P2 zu zeichnen, müssen wir zuerst die Entfernung der beiden Punkte berechnen. Wie wir aus der Mathematik wissen (s. Abb. 14.3 auf der nächsten Seite), können wir Entfernungen durch den Satz des Pythagoras folgendermaßen berechnen:
DIS(P1, P2) = (X1 −X2)2 + (Y1 −Y2)2
Zu diesem Zweck können wir das folgende Programm verwenden:
to ENTF :X1 :Y1 :X2 :Y2
make "DIST sqrt((:X2 - :X1) (:X2 - :X1) + (:Y2 - :Y1)(:Y2 - :Y1))
pr :DIST end
254 |
Lektion 14 Integrierter LOGOund Mathematikunterricht: Vektorgeometrie |
Y2 |
|
|
P2 |
|
|
|
|
|
|
|
Y2 −Y1 |
Y1 |
P1 |
X2 |
−X1 |
|
|||
|
|
X1 |
X2 |
Abbildung 14.3
Jetzt müssen wir noch den Winkel der Strecke zur horizontalen X -Achse bestimmen. Wir sehen in Abb. 14.3, dass
tan(α ) = |
Y2 |
−Y1 |
oder sin(α ) = |
Y2 −Y1 |
|
X2 |
−X1 |
DIST |
|||
|
|
gilt.
Damit wissen wir alles Notwendige, um die Strecke P1P2 zeichnen zu können. Wir schreiben zuerst ein Programm, das für X2 ≥ X1 korrekt arbeitet.
to STRECKE :EINHEIT :X1 :Y1 :X2 :Y2 setpc [0 0 0]
PUNKT :EINHEIT :X2 :Y2
wait 1000 pu bk :X2 :EINHEIT lt 90 bk :Y2 :EINHEIT pd PUNKT :EINHEIT :X1 :Y1
make "DIST sqrt((:X2−:X1) (:X2−:X1) +(:Y2−:Y1) (:Y2−:Y1))
pr :DIST
if :Y2>:Y1 [ make "ABSDY :Y2−:Y1]
[ make "ABSDY :Y1−:Y2] if :X1=:X2 [ make "ALPHA 90 ]
[ make "ALPHA arctan (:ABSDY/abs (:X2-:X1))] setpc [255 0 0]
if :Y2>:Y1 [ lt :ALPHA ] [rt :ALPHA ] fd :DIST :EINHEIT
end
255
Der Befehl abs berechnet für eine gegebene Zahl seinen absoluten Wert, also den positiven Wert der Zahl.
Aufgabe 14.3 Für den Fall Y2 −Y1 > 0 drehen wir lt :ALPHA nach links, weil es der Situation aus Abb. 14.3 auf der vorherigen Seite entspricht. Für den Fall Y2 ≤ Y1 drehen wir nach rechts. Erkläre warum und zeichne das entsprechende Bild analog zu Abb. 14.3.
Aufgabe 14.4 Das Programm STRECKE arbeitet nur für den Fall X2 ≥ X1 korrekt. Erweitere das Programm, so dass es auch für X2 < X1 korrekt arbeitet. Zeichne dazu die entsprechenden Bilder analog zu Abb. 14.3 auf der vorherigen Seite.
Aufgabe 14.5 Erweitere das Programm, so dass die Schildkröte am Ende die Startposition [0,0] in dem Koordinatensystem annimmt. Dabei darfst du den Befehl home nicht verwenden.
Wenn man das Programm STRECKE zur Zeichnung einer Geraden in blauer Farbe modifizieren will, reicht es aus, setpc [255 0 0] gegen setpc [0 0 128] und die letzte Zeile
fd :DIST :EINHEIT
gegen
bk :DIST :EINHEIT fd 3 :DIST :EINHEIT
auszutauschen. |
|
Aufgabe 14.6 Gegeben sind die vier Punkte P1, P2, P3 und P4. Schreibe ein Programm, das rechnerisch und zeichnerisch den möglichen Schnittpunkt der Geraden g1 und g2 bestimmt, wobei g1 durch die Punkte P1 und P2 und g2 durch die Punkte P3 und P4 verläuft.
Aufgabe 14.7 Seien y1 = A ·x + B und y2 = C ·x + D zwei Geraden. Entwickle ein Programm, das für die gegebenen Werte A, B, C und D rechnerisch und zeichnerisch den möglichen Schnittpunkt dieser beiden Geraden bestimmt.
256 |
Lektion 14 Integrierter LOGOund Mathematikunterricht: Vektorgeometrie |
Aufgabe 14.8 Gegeben sind drei Punkte: P1 = (X 1,Y 1), P2 = (X 2,Y 2) und P3 = (X 3,Y 3). Entwickle ein Programm, das Folgendes macht.
a)Das Programm zeichnet alle drei Punkte ein.
b)Falls alle drei Punkte auf einer Geraden liegen, dann zeichnet es diese Gerade.
c)Falls die Punkte nicht auf einer Geraden liegen, zeichnet es das Dreieck P1P2P3.
Aufgabe 14.9 Gegeben ist ein Kreis durch seinen Mittelpunkt M = (XK, YK) und Radius R und eine Gerade y = A ·x + B durch die Werte A und B. Entwickle ein Programm, das zeichnerisch sowie rechnerisch die möglichen Schnittpunkte der Gerade mit dem Kreis bestimmt.
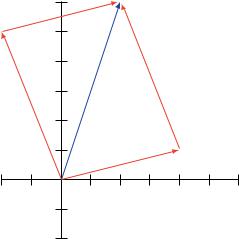
Beispiel 14.2 Es sind zwei Vektoren (X1, Y1) und (X2, Y2) gegeben. Unsere Aufgabe ist es nun, ein Programm zu entwickeln, das die Summe der Vektoren berechnet und graphisch wie in Abb. 14.4 darstellt. In der Zeichnung addiert man die „roten“ Vektoren (4, 1) und (−2, 5) und erhält den blauen Vektor (2, 6) als Resultat. Auch zeichnerisch beobachten wir, dass die Reihenfolge in der Addition keine Rolle spielt.
Abbildung 14.4
Um ein Programm zum Zeichnen der Vektoraddition zu entwickeln, modifizieren wir STRECKE zu STRECKE0 durch die Einführung folgender Zeilen am Ende des Programms:
257
bk :DIST :EINHEIT
if :X2>:X1 [ if :Y2>:Y1 [ rt :ALPHA ] [ lt :ALPHA ] ]
[ if :Y2>:Y1 [ lt 180+:ALPHA ] [ rt 180+:ALPHA ] ]
pu :X1 :EINHEIT lt 90 bk :Y1 :EINHEIT pd
Dadurch wird die Schildkröte nach dem Einzeichnen der Strecke an den Punkt (0, 0) zurückkehren und wie anfangs nach oben schauen. Dann können wir STRECK0 dreimal verwenden, um die beiden roten Vektoren vom Punkt (0, 0) aus und einen der restlichen beiden roten Vektoren zu zeichnen. Danach zeichnen wir mit STRECKE die letzte rote Linie zum Punkt (X1 + X2, Y1 + Y2). Wenn man jetzt die Farbe auf Blau setzt und den Befehl home eingibt, wird der resultierende Vektor blau gezeichnet. Das entsprechende Programm kann wie folgt aussehen:
to VEKTORADD :EINHEIT :X1 :Y1 :X2 :Y2 STRECK0 :EINHEIT 0 0 :X1 :Y1
STRECK0 :EINHEIT 0 0 :X2 :Y2
STRECK0 :EINHEIT :X1 :Y1 :X1+:X2 :Y1+:Y2 STRECKE :EINHEIT :X2 :Y2 :X1+:X2 :Y1+:Y2 setpc [0 0 128] wait 2000
home end
Aufgabe 14.10 Ändere das Programm VEKTORADD, so dass die Schildkröte am Ende die Startposition und die ursprüngliche Blickrichtung einnimmt, ohne jedoch den Befehl home zu verwenden.
Aufgabe 14.11 Entwirf ein Programm, das für einen gegebenen Wert :X (zwischen 0 und 1) den Einheitskreis aus Abb. 14.5 (ohne die Beschriftung X , Y und α ) zeichnet. Damit die Zeichnung grösser dargestellt wird, kannst du für den Einheitskreis einen Radius von 150 Schritten wählen.
Aufgabe 14.12 Zeichne mit einem Programm den Einheitskreis wie in Aufgabe 14.11, aber so dass statt X ,
a)der Wert der Y -Koordinate oder
b)der Winkel α
als Eingabe gegeben ist.
