Gerechtigkeit

459

wo man dann unter „Unterrichtsmaterialien für Informatik“ das „Leitprogramm Ampelsteuerung für drei Siedlungen“ anklicken kann.

Aufgabe 4.1 Projektaufgabe zur Steuerung eines Liftes

Allgemeine Situation In einem Haus mit vier Stockwerken wird ein Lift gebaut, dessen maximale Tragkraft 600 kg ist. In jedem Stockwerk kann man den Lift rufen. Im Fahrstuhl gibt es vier Knöpfe, um die Zieletage bestimmen zu können.

Anforderungen

1.Außer bei einem unvorhergesehenen Andrang darf niemand nach dem Drücken des Anforderungsknopfes lange auf den Fahrstuhl warten.

2.Der Fahrstuhl fährt nicht bei Überlast.

3.Der Fahrstuhl darf nicht mit geschlossenen Türen in einem Stockwerk stehen bleiben, wenn sich in ihm Passagiere befinden.

4.Der leere Fahrstuhl darf nicht in einem Stockwerk warten, obwohl er aus einer anderen Etage gerufen wird.

Gerechtigkeit

1.Niemand soll im Lift nochmals an seiner Einstiegsetage vorbeifahren, ohne vorher in seinem gewünschten Stockwerk anzuhalten.

Deine Aufgabe ist jetzt zuerst, weitere sinnvolle Kriterien für „fairness“ zu formulieren. Danach sollst du in zwei Phasen, wie oben beschrieben, einen Automaten für die Liftsteuerung entwerfen. Dabei darfst du entscheiden, ob der Fahrstuhl einen Überlastsensor oder eine feinere Waage hat. Am Einstieg darf ein Rufknopf sein oder maximal zwei, um die gewünschte Fahrtrichtung anzuzeigen.

Aufgabe 4.2 Projektaufgabe zur Kreuzungssteuerung

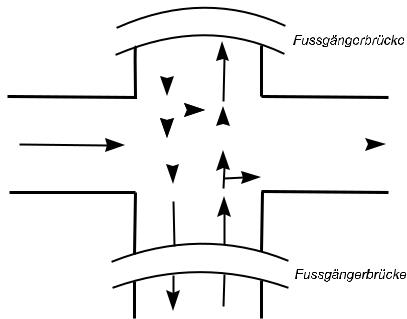
Allgemeine Situation Wir haben eine Kreuzung zwischen einer Einbahnstraße und einer Zweibahnstraße, wie in Abb. 4.2 dargestellt. Es führen zwei Fußgängerbrücken über die Hauptstraße. Man kann die Einbahnstraße an Zebrastreifen überqueren, die mit Ampeln ausgestattet sind. Für den Autoverkehr gibt es Ampeln aus allen Einfahrtsrichtungen. Es sollen Automaten zur Ampelsteuerung an dieser Kreuzung entworfen werden.

Abbildung 4.2

Anforderungen

1.Wenn zwei Verkehrsteilnehmer Grün haben, darf es zu keiner Kollision zwischen beiden kommen.

2.Kein Verkehrsteilnehmer soll bei funktionierender Ampelsteuerung unendlich lange warten.

Gerechtigkeit

1.Es gibt keine Teilnehmer, die unverhältnismäßig länger als andere auf grünes Licht warten müssen.

2.Kein Verkehrsteilnehmer soll bei Rot warten, wenn er der einzige Teilnehmer an der Kreuzung ist.

3.Die stark befahrene Hauptstraße soll Vorfahrt haben, um Fahrzeuge nicht unnötig aufzuhalten oder sogar einen Stau zu provozieren.

461

Freiheitsgrade

1.Du kannst über die Platzierung der Sensoren, wie z. B. Druckknöpfe für Fußgängerampeln, Kameras und Gewichtssensoren, selbst entscheiden.

2.Es ist deine Entscheidung, welche Ampel du vorziehst. Zum Beispiel: Grün für alle aus einer Richtung oder separate Signale für Linksoder Rechtsabbieger.

Entwirf den endlichen Automaten zur Ampelsteuerung dieser Kreuzung in zwei Phasen, wie oben beschrieben.

Aufgabe 4.3 Allgemeine Situation Es gibt zwei Zebrastreifen, die 200 m voneinander entfernt sind. Beide sollen Ampeln erhalten, die durch eine zentrale Steuerung miteinander synchronisiert sind. Zwischen den Zebrastreifen ist ein Halteverbot.

Abbildung 4.3

Anforderungen

1.Es kommt zu keiner Kollision durch gleichzeitiges Grünsignal für zwei Verkehrsteilnehmer.

2.Keiner wartet unendlich lange bei Rot.

Gerechtigkeit

1.Kein Verkehrsteilnehmer muss warten, wenn er der einzige Teilnehmer im System ist.

2.Nach Möglichkeit soll kein Auto zweimal an beiden Übergängen Rot bekommen und dort warten müssen.

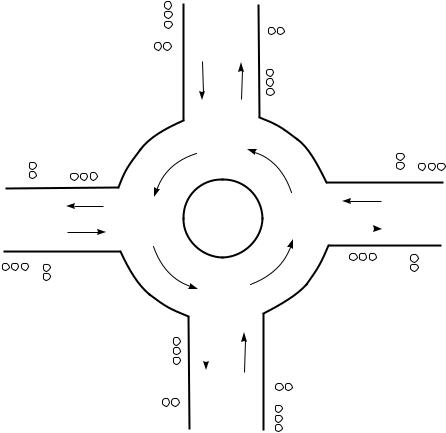
Abbildung 4.4

Aufgabe 4.4 Allgemeine Situation Es gibt einen Kreisverkehr mit vier einmündenden Straßen und der üblichen Vorfahrtsregelung für die Verkehrsteilnehmer, die sich im Kreisel befinden. Eigentlich braucht man keine Ampeln. Jetzt sollen aber in Entfernung von jeweils 100 m auf allen vier Straßen Fußgängerüberwege errichtet werden, so wie in Abb. 4.4 skizziert. Nun soll ein endlicher Automat zur Steuerung aller 16 Ampeln entworfen werden.

Anforderungen

1.Kollisionen zwischen Fußgängern und Fahrzeugen müssen bei korrektem Verhalten aller Teilnehmer ausgeschlossen sein.

2.Keiner darf unendlich lange bei Rot warten.

463

3.Kein Verkehrsteilnehmer soll bei Rot warten, wenn er der einzige Verkehrsteilnehmer im System ist.

Gerechtigkeit

1.Wenn der Kreisverkehr nicht überlastet ist, soll kein Fahrzeug zweimal bei Rot stehen bleiben müssen.

2.Kein Verkehrsteilnehmer soll wesentlich länger bei Rot warten als ein anderer.

Hinweis für die Lehrperson Bei der Durchführung des Projektes in zwei Phasen ist es interessant, auch folgende Variante zu berücksichtigen: Zwei Gruppen können dieselbe Projektaufgabe bearbeiten. Diese Alternative führt zu einer lebhafteren Diskussion nach der ersten Phase. Das Ziel dieser Diskussion ist dann jedoch nicht, sich auf eine Lösung zu einigen. Es sollen vielmehr zwei Lösungsstrategien in die zweiten Phase integriert und am Schluss der Lektion nochmals verglichen werden.

verloren gegangen. Bei großen Programmen ist der Aufwand für einen Korrektheitsbeweis viel umfangreicher als der Aufwand, der mit dem Entwurf des Programms verbunden ist. Deswegen verzichtet man gewöhnlich auf eine vollständige Überprüfung der Korrektheit und beschränkt sich auf die Fehlersuche mittels ausgearbeiteter Testläufe. Daher darf man sich nicht wundern, wenn große Softwaresysteme in der Regel tausende Fehler beinhalten, die in gewissen Spezialfällen1 auftreten können. Solche selten auftretenden Fehler sind innerhalb komplexer Systeme schwer und aufwendig zu finden, weshalb man gewöhnlich zuerst auf ihre Suche verzichtet. Erst wenn sie zu einem falschen Verhalten in den laufenden Anwendungen führen, wird versucht sie zu beheben.

Bei endlichen Automaten ist die Sachlage oft anders. Endliche Automaten benutzt man für die Steuerung von Verkaufsautomaten, Ampeln, Aufzügen usw. Ein entworfener Automat wird oft in Hardware integriert und tausendfach vervielfältigt. Ein fehlerhaftes Verhalten in den vielen Kopien hätte dann große ökonomische Konsequenzen. Daher lohnt sich die Investition in die vollständige Überprüfung der Korrektheit.

Hinweis für die Lehrperson Diese Lektion eignet sich sehr gut für das Üben der Führung von Induktionsbeweisen. Man kann kaum einfachere Aufgaben zu Induktionsbeweisen finden als bei der Verifikation von endlichen Automaten. Die Voraussetzung für eine erfolgreiche Bearbeitung nachfolgender Lektionsteile ist das Verständnis des Begriffs der Implikation, so wie wir ihn im Modul „Geschichte und Begriffsbildung“ eingeführt haben.

Bei endlichen Automaten werden wir die Korrektheitsbeweise mittels Induktion durchführen. Deswegen rekapitulieren wir jetzt zuerst die Induktionsbeweise.

Mit Induktionsbeweisen belegt man die Gültigkeit einer gegebenen Behauptung für alle natürlichen Zahlen. Das Schema des Induktionsbeweises sieht wie folgt aus:

Sei B(i) eine Behauptung für eine natürliche Zahl i. Unsere Zielsetzung2 ist

B(i) gilt für alle i N

zu beweisen. Beachte, dass N unendlich ist und wir nicht unendliche viele, einzelne Beweise für jedes i durchführen können.

Den Beweis führt man in diesen zwei Schritten aus:

1Oft sind es Fälle, mit denen niemand gerechnet hat.

2Es gibt auch allgemeinere Darstellungen von Induktionsbeweisen als die hier präsentierten.

469

Sprache L und einen konstruierten EA A zu beweisen? Oder genauer gesagt: „Was hat die Behauptung L = L(A) mit der Induktion zu tun?“

Der erste Ansatz ist, L = L(A) nicht direkt zu beweisen, aber ein allgemeineres Resultat zu zeigen, dessen Folge L = L(A) ist. Wir bestimmen für jeden Zustand q von A die entsprechende Wortklasse Klasse(q) und beweisen die Richtigkeit dieser Bestimmung. Den Beweis führen wir mittels Induktion bezüglich der Wortlänge. Dies bedeutet, die Gültigkeit der Klassenzuordnung zuerst für kurze Wörter zu beweisen und sie dann durch den Induktionsschritt auf alle Wörter zu erweitern.

Beispiel 5.2 Betrachten wir die folgende Sprache

L = {x {0, 1} | |x|0 mod 4 ist gerade}.

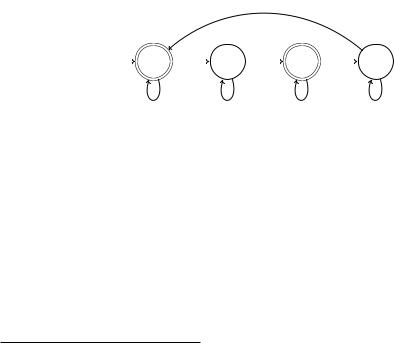
Gemäß Abschnitt 3.3 reichen vier Zustände aus, um die Reste nach der Teilung der Anzahl Nullen in x modulo 4 speichern zu können. Wir erhalten dann den EA A aus Abb. 5.1.

gilt.

Sei Hyp(i) die Behauptung, dass diese Klassenzuordnung korrekt4 für Wörter der Länge

4Formal ausgedrückt, für alle i = 0, 1, 2, 3 gilt

Klasse[qi] ∩{0, 1}i = Resti ∩{0, 1}i = x {0, 1}i | |x|0 mod 4 = i .

471

(i)Sei x = y1 für ein y {0, 1}n−1.

Weil y die Länge n −1 hat, ist y nach Hyp(n −1) unserer Hypothese folgend

in der richtigen Klasse. Also wenn y Rest j für ein j {0, 1, 2, 3} gilt, dann ist laut der Induktionshypothese Hyp(n −1) y Klasse[q j ]. Weil

x = y1 und somit |x|0 = |y|0 ,

ist, liegt x auch in der Klasse Rest j . Wir brauchen also nur zu zeigen, dass auch x Klasse[q j ] ist. Dies ist aber offensichtlich, weil δA(qi, 1) = qi für alle i {0, 1, 2, 3} gilt (beim Lesen einer 1 wird der Zustand nicht geändert). Damit impliziert

(q0, y) A (q j , λ )

direkt die folgende Berechnung von A auf x = y1:

(q0, y1) A (q j , 1) A (q j , λ )

und somit ist x Klasse[q j ].

(ii) Sei x = y0 für ein y {0, 1}n−1.

Sei |y|0 mod 4 = j für ein j {0, 1, 2, 3}, (d.h. y Rest j ). Weil |y| = n −1 ist, liefert uns die Induktionshypothese Ind(n −1), dass y Klasse[q j ].

(ii.1) Betrachten wir zuerst den Fall j {0, 1, 2}.

{weil j {0, 1, 2}}.

Damit ist x in Rest j+1.

Wir müssen zeigen, dass x Klasse[q j+1] ist. Dies ist aber offensichtlich,

j+1 für alle j {0, 1, 2} gilt. Daraus ergibt sich die folgende Berechnung von A auf x = y0

(q0, y0) A (q j , 0) A (q j+1, λ ).

(ii.2) Es bleibt noch der Fall j = 3 übrig. Die Vervollständigung des Beweises dafür wird dem Leser überlassen.

Wenn man den vorgestellten Beweis der Korrektheit des endlichen Automaten in Beispiel 5.2 betrachtet, dann sieht man, dass im Induktionsschritt jede gerichtete Kante des Automaten genau einmal überprüft wird. Mit „Überprüfung“ ist gemeint, dass man den Beweis in genauso viele Fälle zerlegen kann, wie es Kanten gibt. Die einzelnen Kanten werden folgendermaßen überprüft:

Wenn x {0, 1}n−1 nach Hyp(n − 1) in einer Klasse[q] ist, dann sind auch x0 und x1 dank korrektem δ (q, 0) = r und δ (q, 1) = s in der richtigen Klasse.

Aufgabe 5.4 Führe den Induktionsschritt ausführlich für den Fall (ii.2) durch.

Aufgabe 5.5 Ist der EA in Abb. 5.1 der kleinste Automat für

L = {x {0, 1} | |x|0 mod 4 ist gerade}?

Falls nicht, entwirf einen EA für L mit weniger Zuständen und beweise seine Korrektheit.

Aufgabe 5.6 Entwirf endliche Automaten für folgende Sprachen und beweise mittels Induktion die Korrektheit dieser Automaten:

(a){x {0, 1} | |x|1 mod 3 = 0},

(b){x {0, 1, 2} | |x| ≥ 3},

(c){x {0, 1} | |x| ist gerade},

(d){x {0, 1} | |x| ist ungerade und x = 1y für ein y {0, 1} },

(e){x {0, 1, 2} | |x|2 mod 5 {1, 2, 4}},