473

(f){x {0, 1, 2} | 2 ≤ |x| ≤ 5},

(g){x {0, 1, 2} | |x| ≤ 3 oder |x| ≥ 6}

(h){x {a, b} | (|x|a −|x|b) mod 4 = 1}.

Zusammenfassung

Unter der Verifikation eines endlichen Automaten M verstehen wir eine Überprüfung der richtigen Funktionalität von M. In der formalen Umsetzung zeigt man, dass L(M) die Sprache ist, die man erkennen will.

Die Verifikation führen wir meistens mittels Induktionsbeweisen durch. Man verwendet sie, um die Gültigkeit einer konkreten Behauptung B(i) für alle natürlichen Zahlen i zu belegen. Im Fall von Induktionsbeweisen der Korrektheit werden die Beweise anhand der Eingabelänge durchgeführt. Im Induktionsschritt zeigen wir, dass ein endlicher Automat, der sich bei allen Wörtern mit einer maximalen Länge n −1 korrekt verhält, auch richtig auf Eingaben der Länge n reagiert. Durch diesen Beweis wird im Prinzip jede einzelne Kante des Automaten dahingehend überprüft, ob sie zwei Zustandsklassen korrekt verbindet.

Kontrollfragen

1.Warum ist die Verifikation von Informatikprodukten wichtig?

2.Aus welchen zwei Schritten besteht ein Induktionsbeweis?

3.Wie ist die allgemeine Strategie für den Beweis der richtigen Funktionalität eines entworfenen endlichen Automaten?

4.Sei M ein endlicher Automat mit m Zuständen, der über dem Alphabet Σ arbeitet. Warum kann man den Beweis des Induktionsschrittes auf m ·|Σ| viele Fälle verteilen?

Kontrollaufgaben

1. Beweise mittels Induktion, dass für alle positiven ganzen Zahlen 22n > 2n gilt. Kann man

n

diese Tatsache elegant und ohne Induktionsbeweis begründen?

2.Entwirf jeweils einen endlichen Automaten für die folgenden Sprachen und beweise seine Korrektheit!

a){x111y | x, y {0, 1} },

b){x {a, b} | (|x|a −2|x|b) mod 3 = 0},

c){011, 101, λ }.

Lösungen zu ausgesuchten Aufgaben

Aufgabe 5.1 (ii)

Für alle n N −{0} haben wir die folgende Induktionshypothese

n

HYP(n): ∑2i = 2n+1 −1

i=0

Schritt 1 Wir beweisen HYP(1)

1

∑2i = 20 + 21 = 3

i=0

Andererseits 21+1 −1 = 22 −1 = 3. Wir sehen, dass HYP(1) gilt.

Schritt 2 Wir setzen voraus, dass HYP(1), HYP(2), ... , HYP(n-1) gelten und beweisen, dass auch HYP(n) gilt. Bemerke, dass die Aussage von HYP(n-1) folgender Behauptung entspricht:

n−1

∑ 2i = 2(n−1)+1 −1 = 2n −1.

i=0

Jetzt rechnen wir wie folgt:

n−1 ∑ni=0 2i = 2n + ∑ 2i

i=0

= 2n + 2n −1

{weil HYP(n-1) gilt}

= 2 ·(2n) −1 = 2n+1 −1.

Damit haben wir gezeigt, dass die Gültigkeit von HYP(n-1) die Gültigkeit von HYP(n) impliziert. Dies vervollständigt den Induktionsbeweis.

endliche Automaten für einzelne Worteigenschaften zu entwerfen und dann aus diesen Automaten den endlichen Automaten für die gegebene Sprache zu bauen? Die Antwort ist positiv, denn man kann einen EA bauen, der die Arbeit zweier oder mehrerer endlicher Automaten simulieren kann. Um das zu verstehen, widmen wir uns zuerst dem Begriff „Simulation“.

Der Begriff Simulation hat in der Informatik eine breitgefächerte Bedeutung, die auf der unterschiedlichen Auslegung dieses Begriffs beruht. Eine sehr weitgefasste Interpretation von Simulation ist die Blackbox-Simulation. Man simuliert ein Verfahren (Programm) so, dass das Eingabe-Ausgabe Verhalten übereinstimmt. Ein Programm A simuliert also ein Programm B, wenn A jeweils dieselben Resultate wie B liefert, unabhängig davon, durch welche Rechnerwege die Resultate ermittelt worden sind. Die engste und härteste Auslegung von Simulation fordert, dass jeder elementare Schritt des simulierten Programms durch genau einen Schritt des simulierenden Programms widergespiegelt wird.

Nachfolgend wird Simulation im engen Sinn gedeutet, weil wir nach dem Lesen jedes einzelnen Buchstabens wissen müssen, welche Merkmale (Eigenschaften) das bisher gelesene Präfix hat oder eben nicht hat.

Hier wird jetzt der Ansatz verfolgt, zwei endliche Automaten durch nur einen EA zu simulieren. Seien M1 und M2 zwei endliche Automaten mit den Zustandsmengen Q1 und Q2 und L1 = L(M1) und L2 = L(M2). Wir konstruieren einen neuen endlichen Automaten M mit der Zustandsmenge

Q = Q1 ×Q2 = {(q, p) | q Q1 und p Q2}.

Ein Zustand von M besteht also aus zwei Teilen. Der erste Teil entspricht dem Zustand von M1, der zweite Teil dem Zustand von M2. Auf diese Weise kann M in seiner Konfiguration die vollständige Information über die beiden aktuellen Konfigurationen von M1 und M2 erhalten. Dies ist in Abbildung 6.1 anschaulich dargestellt. M1 ist in der Konfiguration (q, xi . . . xn) und M2 ist in der Konfiguration (p, xi . . . xn). Diese Information ist in der Konfiguration ((q, p), xi . . . xn) von M vollständig enthalten. Die Berechnungsschritte

(q, xixi+1 . . . xn) M1 (v, xi+1 . . . xn) und (p, xixi+1 . . . xn) M2 (s, xi+1 . . . xn)

von M1 und M2 simuliert M durch den Schritt

((q, p), xixi+1 . . . xn) M ((v, s), xi+1 . . . xn).

M geht aus dem Zustand (q, p) beim Lesen des Symbols xi in den Zustand (v, s) genau dann über [δM ((q, p), xi) = (v, s)], wenn

477

Abbildung 6.1

1.M1 aus q beim Lesen von xi in v übergeht [δM1 (q, xi) = v], und

2.M2 aus p beim Lesen von xi in s übergeht [δM2 (p, xi) = s].

Illustrieren wir diese Simulationsidee mit folgendem Beispiel:

Beispiel 6.1 Seien L1 = {x {0, 1} | |x|0 ist gerade}, und L2 = {x {0, 1} | |x|1 = 0 oder |x|1 ≥ 3}. Wir bauen zuerst zwei endliche Automaten M1 und M2 mit L(M1) = L1

und L(M2) = L2, die in Abbildung 6.2 und Abbildung 6.3 dargestellt sind.

q0 1

00

q1 1

Abbildung 6.2 M1

Dem Ansatz folgend, hat M die Zustandsmenge

{(q0, p0), (q0, p1), (q0, p2), (q0, p3), (q1, p0), (q1, p1), (q1, p2), (q1, p3)}.

478 Lektion 6 Simulation und modularer Entwurf endlicher Automaten

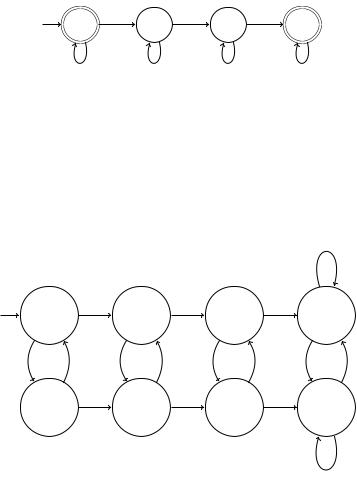
Um M übersichtlich zeichnen zu können, werden die Zustände von M auf einem Blatt Papier matrixartig angelegt (Abbildung 6.4). Die erste Zeile beinhaltet Zustände mit der ersten Komponente q0 und die zweite Zeile Zustände mit q1 als erste Komponente. Die i-te Spalte für i = 0, 1, 2, 3 umfasst die Zustände mit der zweiten Komponente pi.

1

Abbildung 6.4 M

Jetzt muss man anhand von M1 und M2 die Kanten (Übergänge) bestimmen. Beispielsweise geht M1 aus q0 bei 0 in q1 über und M2 bleibt beim Lesen von 0 in p0. Deswegen geht M aus (q0, p0) beim Lesen von 0 in (q1, p0) über.

Nachdem auf diese Weise alle Kanten gezeichnet worden sind, zeigt die Abbildung 6.4, wie man in den Spalten die Anzahl der Nullen modulo 2 rechnet und in den Zeilen die Anzahl Einsen von 0 bis 3 zählt. Also bedeutet der Zustand (qi, p j ) für i {0, 1}, j {0, 1, 2, 3}, dass das bisher gelesene Präfix x genau j Einsen beinhaltet (wenn j = 3 mindestens drei Einsen hat) und |x|0 mod 2 = i. Damit wurden alle für uns

Aufgabe 6.1 Betrachte M aus Beispiel 6.1. Bestimme die Menge der akzeptierenden Zustände, wenn M die folgenden Sprachen akzeptieren soll.

a)L(M1) −L(M2) = {x {0, 1} | x L(M1) und x / L(M2)}

b)L(M2) −L(M1)

c){0, 1} −(L(M1) ∩L(M2))

d){0, 1} −(L(M1) L(M2))

e)({0, 1} −L(M1)) L(M2)

f)({0, 1} −L(M2)) ∩L(M1).

Hinweis für die Lehrperson An dieser Stelle empfehlen wir die Verwendung der PuzzleMethode. Die Klasse sollte in kleine Gruppen aufgeteilt werden. Jede Gruppe soll einen Automaten aus der nachfolgenden Aufgabe bauen. Am Ende muss jede Gruppe das Resultat und insbesondere ihre Überlegungen im Prozess des Automatenentwurfs der übrigen Klasse in einem Vortrag schildern.

Aufgabe 6.2 Nutze die Methode des modularen Entwurfs, um endlichen Automaten für folgende Sprachen zu bauen:

a){x {0, 1} | |x|0 mod 3 = 1 und |x|1 mod 3 = 2}

b){x {0, 1} | |x|0 mod 2 = 1 und 1 ≤ |x|1 ≤ 3}

c){x {0, 1, 2} | |x|0 mod 3 {0, 1} und (|x|1 + |x|2) mod 2 = 0}

d){x {0, 1} | |x|1 ist gerade und x enthält das Teilwort 0101}

e){x {0, 1} | x = y00z11v für y, z, v {0, 1} und |x|0 mod 3 = 2}

f){x {0, 1, a, b} | x enthält das Teilwort 111 oder x ent-

hält das Teilwort aba}

g) {x {0, 1} | x beginnt mit dem Präfix 011 und x enthält 100 als Teilwort}

h) {x {0, 1} | x enthält entweder 0101 als Teilwort oder endet mit dem Suffix 111}

als formale Sprache zu üben. Wenn man eine Konstruktion exakt beschrieben hat, kann man sie durch ein Programm implementieren und es dann dem Rechner überlassen, automatisch endliche Automaten aus schon bestehenden Automaten zusammenzusetzen. Zusätzlich kann man, wenn man eine exakte Beschreibung eines Automaten hat, formal seine Korrektheit im Allgemeinen beweisen. Auf diese Weise vereinfacht der modulare Entwurf die komplette Verifikation. Es reicht aus, die Korrektheit der einfachen endlichen Automaten aus Basismodulen zu beweisen. Die Korrektheit der erzeugten komplexen EA resultiert dann direkt aus dem allgemeinen Korrektheitsbeweis der angewendeten Konstruktion.

Beschreiben wir also formal den EA M, der zwei gegebene Automaten

M1 = (Q1, Σ, δ1, q01, F1) und M2 = (Q2, Σ, δ2, q02, F2)

simuliert. Beide arbeiten über dem gleichen Alphabet Σ. Ansonsten hat jeder EA Mi (i = 1, 2) eine eigene Zustandsmenge Qi, einen eigenen Anfangszustand q0i, eine eigene Transitionsfunktion δi und eine eigene Menge der akzeptierenden Zustände Fi. Um Missverständnisse zu vermeiden ist es sinnvoll, unterschiedliche Namen für die Zustände in M1 und M2 zu verwenden. Dazu wählt man die Namen so, dass Q1 ∩Q2 =0/ gilt.

Wir konstruieren den EA M wie folgt:

M = (Q, Σ, δ , q0, F ),

wobei

1.Q = Q1 × Q2 = {(q, p) | q Q1, p Q2}, d. h. die Zustände von M sind Paare (2-dimensionale Vektoren), wobei das erste Element ein Zustand von M1 und das zweite Element ein Zustand von M2 ist.

2.Σ ist dasselbe Eingabealphabet, wie M1 und M2 es benutzen.

3.q0 = (q01, q02), d.h. der Startzustand von M ist das Paar (Startzustand von M1, Startzustand von M2).

4.Für alle q Q1, p Q2 und alle a Σ

δ ((q, p), a) = (δ1(q, a), δ2(p, a)),

d.h. beim Lesen eines Buchstabens a Σ ändert M das erste Element q seines derzeitigen Zustands (q, p), genauso wie es M1 beim Lesen von a geändert hätte.

483

Das zweite Element p des Zustands (q, p) wird nach der Transitionsfunktion δ2 von M2 geändert.

5.Die Wahl von F hat mit der eigentlichen Simulation nichts zu tun. F bestimmt nur die Sprache, die akzeptiert werden soll. Wenn

L(M) = L(M1) L(M2)

erwünscht ist, dann setzen wir

F = F1 ×Q2 Q1 ×F2.

Auf diese Weise akzeptiert M genau dann, wenn mindestens einer der Automaten M1 und M2 das gegebene Wort akzeptiert. Wenn man

L(M) = L(M1) ∩L(M2)

fordert, dann setzen wir

F = F1 ×F2.

Somit akzeptiert M ein Wort x genau dann, wenn beide Automaten M1 und M2 das Wort x akzeptieren.

Aufgabe 6.4 Betrachte die Sprachen

L1 = {x {0, 1} | |x|0 mod 3 = 2},

L2 = {x = y011z | y, z {0, 1} }.

Konstruiere endliche Automaten M1 und M2 mit L(Mi) = Li für i = 1, 2. Gib für beide Automaten die formale Beschreibung der Transitionsfunktionen δ1 und δ2 in Tabellenform an. Wende die oben gegebene Konstruktion (Teil 4) an und konstruiere die Tabelle für die Transitionsfunktion δ von M.

Aufgabe 6.5 Wie muss man F in Teil 5 der Konstruktion wählen, wenn man

a)L(M) = L(M1) −L(M2) = {x Σ | x L(M1) und x / L(M2)},

b)L(M) = L(M2) −L(M1),

c)L(M) = Σ −(L(M1) ∩L(M2)),

d)L(M) = Σ −(L(M1) L(M2))

akzeptieren will?

die Berechnung von M auf w ist.

Betrachten wir jetzt die Berechnungen von M1, M2 und M auf x = wa. Die Berechnungen von M1 und M2 auf x kann man aus (6.1) folgendermaßen erweitern:

(q01, wa) M1 (q, a) M1 (δ1(q, a), λ ), (q02, wa) M1 (p, a) M2 (δ2(p, a), λ ).

Weil wir in der Konstruktion von M (Teil 4) δ durch

δ ((q, p), a) = (δ1(q, a), δ2(p, a))

definiert haben und (6.2) gilt, muss die Berechnung von M auf x = wa wie folgt aussehen:

((q01, q02), wa) M ((q, p), a) M ((δ1(q, a), δ2(p, a)), λ ).

Damit haben wir gezeigt, dass M die Berechnung auf x in dem Zustand

(δ1(q, a), δ2(p, a))

beendet. Dies ist das gewünschte Ergebnis, weil M1 in δ1(q, a) und M2 in δ2(p, a) endet.

Aufgabe 6.8 Betrachte die Sprachen L1 und L2 aus Aufgabe 6.4 und die dazu konstruierten endlichen Automaten M1, M2 und M. Führe einen Induktionsbeweis der Behauptung durch, M simuliere die Automaten M1 und M2. Du sollst also den allgemeinen Beweis der Korrektheit der Konstruktion (Satz 6.1) an einem konkreten Beispiel durchführen.