
7 (НСВ)
.pdfМетодические рекомендации для студентов 1 курса лечебного, медико-профилактического и педиатрического
факультетов по самоподготовке и проведению практического занятия
по математике
Тема: Непрерывные случайные величины и их характеристики. Нормальный закон распределения. Вероятность попадания в заданный интервал.
Актуальность темы: ознакомление с основными понятиями и методами теории вероятностей и случайных величин как средств решения задач физического, химического, биологического и иного характера, встречающихся как в процессе изучения профильных дисциплин, так и в дальнейшей профессиональной деятельности
Цель занятия:
1.научиться по функции распределения находить плотность распределения вероятностей непрерывной случайной величины и наоборот, вычислять числовые характеристики непрерывных случайных величин
2.научиться вычислять числовые характеристики нормальных случайных величин, вычислять вероятность попадания в интервал непрерывной случайной величины, распределенной по нормальному закону
План изучения темы
1.Случайные величины: дискретная и непрерывная.
2.Числовые характеристики непрерывной случайной величины.
3.Плотность и функция распределения непрерывной случайной
величины.
4.Основные параметры нормального распределения непрерывной случайной величины.
5.Вероятность попадания возможных значений непрерывной случайной величины, распределенной по нормальному закону в заданный интервал
Рекомендуемая литература:
Основная литература:
1. Морозов, Ю.В. Основы высшей математики и статистики: учеб. для студентов мед. и фаpмацевт. вузов и фак./Ю.В. Морозов.-М.:Медицина,
2004.-232 с.
2. Основы высшей математики и математической статистики: учеб. для студентов мед. и фармацевт. вузов/И.В. Павлушков, Л.В.Розовский, А.Е.Капульцевич и др.-2-е изд., испр.-М.:ГОЭТАР-Медиа, 2006.-423 с.
Дополнительная литература:
Методические рекомендации к практическим занятиям по высшей математике [Электронный ресурс]: учеб.-метод. пособие для вузов/ авт.-сост. : Т.А.Новичкова; ГОУ ВПО "Курск. гос. мед. ун-т", каф. физики, информатики и математики.-Курск:КГМУ, 2009.
Гмурман В.Е. Теория и математическая статистика. М. «Высшая школа»,
изд. 5, 2004.
Вопросы для самоконтроля:
1.Понятие непрерывной случайной величины.
2.Интегральная функция распределения случайной величины (определение).
3.Нахождение вероятности попадания случайной величины в заданный интервал через функцию распределения.
4.Дифференциальная функция распределения. Вероятность попадания случайной величины в заданный интервал. Условие нормировки.
5.Числовые характеристики непрерывных случайных величин, формулы для их нахождения. Вероятностный смысл математического ожидания. Назначение дисперсии и среднего квадратичного отклонения.
6.Закон нормального распределения, кривая Гаусса.
7.Нормированное нормальное распределение. Функция распределения нормированной нормально распределенной случайной величины.
8.Вероятность попадания нормально распределенной случайной величины в заданный интервал.
9.Нахождение вероятности попадания случайной величины в заданный интервал через функцию распределения.
10.Дифференциальная функция распределения. Вероятность попадания случайной величины в заданный интервал. Условие нормировки.
11.Закон нормального распределения, кривая Гаусса.
12.Нормированное нормальное распределение. Функция распределения нормированной нормально распределенной случайной величины.
13.Вероятность попадания нормально распределенной случайной величины в заданный интервал.
Задания на самоподготовку:
2.Непрерывная случайная величина задана функцией распределения
0, если х≤1
F(x) = {а(х 1) , если 1<x≤3 1, если х>3
Требуется а) найти постоянную а
б) найти плотность распределения f(x) в) построить графики f(x) и F(x)
г) найти Р(1,5<х<2)
д) найти параметры распределения
3. Пусть случайная величина Х имеет нормальное распределение с математическим ожиданием μ=15 и средним квадратическим отклонением σ=1. найти интервалы для Х, если вероятность интервала | Х - μ| < ε равна 0,95.
Ориентировочные основы действий:
1.Изучить основные понятия по теме
2.Ответить на вопросы для самоконтроля
3.Проработать примеры решения задач по теме
4.Выполнить задания для самостоятельного контроля
5.Решить контрольные задания по теме
После изучения данной темы студент должен знать: понятия функции и плотности распределения вероятности случайных
величин, научиться определять числовые характеристики непрерывных случайных величин и вероятность попадания значений случайной величины в заданный интервал.
уметь: составлять функцию распределения непрерывной случайной величины, строить её график, определять числовые характеристики: математическое ожидание, дисперсию, среднее квадратическое отклонение, находить с помощью функции распределения вероятность событий, определять вероятность попадания значений нормально распределенной случайной величины в заданный интервал.
Краткая теория
Функцией распределения (интегральной функцией) непрерывной случайной величины Х называется функция F(х), равна вероятности P(Х<х) того, что случайная величина приняла значение меньше х
F(х) = P(Х<х)
Свойства:
1. |
0 F X 1 |
(из определения вероятности)
2. F(х) – неубывающая функция
3. Вероятность попадания случайной величины Х в полуинтервал [a,b) равна разности между значениями функции распределения в правом и левом концах интервала (a,b)
P(a x b) F b F a
4. Вероятность того, что случайная величина Х примет заранее заданное значение а равна нулю
P(X a) 0
5. Если возможные значения непрерывной случайной величины расположены на всей числовой оси, то

lim F X 0, |
lim |
F X 1 |
x - |
x |
|
Плотностью распределения (плотностью вероятности) непрерывной случайной величины Х называют функцию f(x), равную производной её интегральной функции f(X) F' X
f(x)
a |
b |
x |
|
Свойства:
1. f(x) – функция неотрицательная, т.к. F(x) – неубывающая, то
F’(x)=f(x)≥0
2. Вероятность того, что непрерывная случайная величина Х в результате испытания примет какое-нибудь значение из интервала (a,b) равна определенному интегралу плотности вероятности в пределах от a и b.
P a
3.
4.
|
b |
|
|
X b f(x)dx F(b) F(a) |
|||
|
a |
|
|
|
|
|
|
|
f(x)dx |
1 |
- условие нормировки плотности вероятностей |
|
|||
- |
|
|
|
|
x |
|
|
F(X) f(x)dx |
|||
|
- |
|
|
Числовые характеристики непрерывных случайных величин
Математическое ожидание
Дисперсия
M( X ) x f (x)dx
|
|
|
|
|
|
|
|
|
|
|
D( X ) 2 |
|
x 2 f (x)dx x2 f (x)dx 2 x |
||||||||
M X |
|
|
|
M X |
|
|
|
|
||
2 |
2 |
2 |
|
2 |
2 |
2 |
|
|||
|
|
|
|
|
|
|||||
Среднее квадратическое отношение (X )
f (x)dx 2 f (x)dx

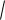 D X
D X
Модой М0(x) непрерывной случайной величины Х называется то её возможное значение, которому соответствует локальный максимум плотности распределения.
В частности, если распределение имеет два локальных максимума, то его называют бимодальным.
Медианой Ме(х) непрерывной случайной величины Х называют её
возможное значение, которое определяется равенством. |
||
P X M |
X P X M |
X |
e |
e |
|
Геометрически медиану можно истолковать как точку, в которой ордината f(x) делит пополам площадь, ограниченную кривой распределения.
Равномерное распределение Непрерывная случайная величина Х имеет равномерное
распределение вероятностей на отрезке [a,b], если её плотность вероятности на [a,b] постоянна, а вне интервала равна нулю, т.е.
f(x)
0, x a |
|||
|
|
1 |
|
|
|
, a x b |
|
f x |
b |
a |
|
|
|
||
|
|
|
|
0, x b |
|||
|
|
|
|
1 b-a
|
|
|
|
a |
b |
x |
|
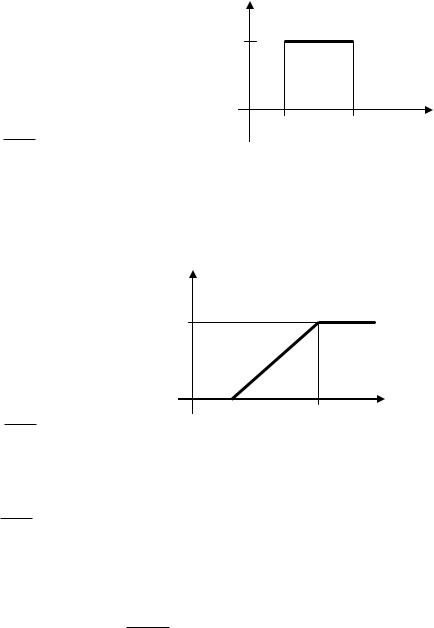
Функция распределения случайной величины Х, распределенной по равномерному закону
F(x)
0, x a |
|
|||||
|
|
a |
|
|
||
x |
, a x b |
|||||
F x |
b |
a |
||||
|
|
|
||||
|
|
|
|
|
||
1, x b |
|
|||||
|
|
|
|
|
|
|
|
a b |
|
|
2 |
||
M x |
, D x |
b a |
||||
|
2 |
12 |
||||
|
|
|
|
|||
1
|
|
|
|
0 |
a |
b |
x |
|
|
Вероятность попадания величины Х, распределенной по равномерному закону на [a,b] в интервал (х1, х2) равна
|
|
|
|
x |
2 |
|
x |
x |
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
P x |
x x |
|
|
|
|
f (x)dx |
2 |
1 |
|
|
|
b a |
|||||
|
|
|
|
x |
|
|||
|
|
|
|
|
1 |
|
|
|
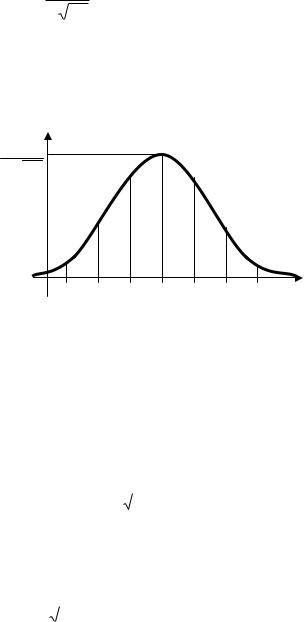
Нормальный закон распределения (закон Гаусса)
Закон распределения вероятностей непрерывной случайной величины Х называют нормальным, если плотность вероятности определяется формулой
f x |
|
1 |
|
|
2 |
||
|
|
|
x |
|
|
|
|
2 |
e |
|
2 |
2 |
|
|
||
|
|
|
|
, где μ – мат. ожидание сл.вел. Х, σ – ср.кв. отклонение
сл.вел. Х.
График функции y=f(x) называют нормальной кривой распределения или
кривой Гаусса.
f(x)
1

 2
2
μ-3σ |
μ |
μ+3σ x |
|
Площадь фигуры, ограниченной кривой Гаусса и двумя прямыми х = а и х = b, где a<b, представляет собой вероятность того, что сл.вел. Х лежит между а и b,
т.е.
b P a X b f(x)dx
a
Нормальное распределение с параметрами μ=0, σ=1 называют
нормированным или стандартным.
Функция x |
|
1 |
|
|
|
x 2 |
|
|
|
|
|||
|
|
|
e |
2 |
||
|
|
|
||||
2π |
|
|
||||
|
|
|
|
|
|
|
называется плотностью вероятности
нормированного (стандартного) распределения.
Функция распределения стандартного распределения есть
|
|
1 |
|
x |
x 2 |
|
Ф x |
|
|
e |
|
|
|
|
|
2 dx функция Лапласа |
||||
|
|
|
||||
|
||||||
|
|
2π |
|
|
||
|
|
|
|
|
|
|
Вероятность попадания в заданный интервал нормальной случайной величины
Известно, что если случайная величина Х задана плотностью распределения f(x), то вероятность того, что Х примет значение, принадлежащее интервалу (a,b) равна
b |
b |
a |
|||||
P a X b f(x)dx Ф |
|
|
Ф |
|
, где Ф(х) – функция Лапласа. |
||
|
|
||||||
a |
|
|
|
|
|||

Используя полученную формулу можно также вычислить вероятность того, что отклонение нормально распределенной случайной величины Х от её математического ожидания по абсолютной величине меньше заданного положительного числа ε, равна
|
|
|
|
P X 2Ф |
|
|
1 |
|
|||
|
|
|
|
Правило «трех сигм»: практически все возможные значения случайной величины, подчиненной нормальному закону с параметрами μ (математическое ожидание) и σ(среднее квадратическое отклонение), (коротко: Х ~ N(μ, σ)) заключены в интервале:
(μ - 3σ; μ + 3σ).
Примеры решения задач
Пример 1 .
Дана плотность вероятности случайной величины Х
0, x 0 |
|
|
x |
f x a sin x,0 |
|
|
|
0, x |
|
|
|
.
Определить коэффициент а, функцию распределения F(x), построить график F(x), f(x).
Решение. Используя условие нормировки, можно найти коэффициент а
|
0 |
|
|
|
|
||
f(x)dx |
0dx |
asinxdx |
0dx 1 |
||||
- |
- |
0 |
|
|
|
||
Первый и последний интегралы равны нулю, второй находим по таблице |
|||||||
интегралов. |
|
|
|
|
|
||
a cos cos 0 1 |
|
|
|
||||
a |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||
2 |
|
|
|
|
|
|
|
|
|
|
|
0, x 0 |
|
||
|
|
|
|
|
1 |
|
|
Следовательно, |
|
sin x,0 |
x |
||||
f x |
2 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
0, x |
|
||
|
|
|
|
|
|
|
|
2. Находим функцию распределения F(x) на трех интервалах, так как функция плотности принимает три различных значения на данных интервалах,
|
|
x |
|
используя свойство: |
F ( x) |
|
f ( x)dx |
|
|||
|
|
|
|
интеграл всегда х).
Первый интервал: x ≤ 0.
x
F(X) 0dx 0
-
(заметим, что верхний предел в данном
Второй интервал: 0 < x ≤ π.
0 |
x |
1 |
|
1 |
cos x |
|
F(X) |
0dx |
sinxdx |
x |
|||
2 |
2 |
0 |
||||
- |
0 |
|
|
|
||
|
|
|
|
|
Третий интервал: x > π.
|
1 |
cos x cos 0 |
1 |
cos x 1 |
1 |
|
1 |
cos x |
|
2 |
2 |
2 |
2 |
||||||
|
|
|
|
|
0 |
|
1 |
x |
|
F(X) 0dx |
sinxdx 0dx |
|||
2 |
||||
- |
0 |
|
||
|
||||
1 |
cos cos 0 1 |
|
2 |
||
|
Итого,
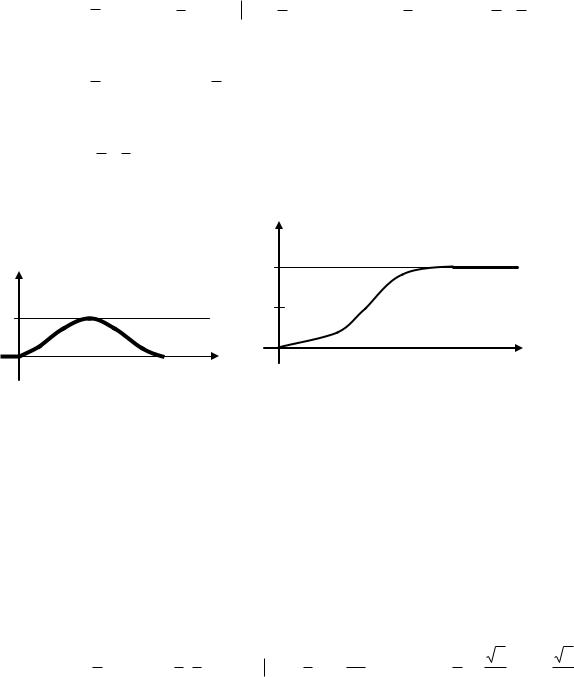
f(x)
1
2
0, x 0 |
|
||||
|
1 |
|
1 |
|
|
|
|
cos x,0 |
x |
||
F(X) |
2 |
2 |
|||
|
|
|
|
||
1, x |
|
||||
|
|
|
|
|
|
F(x)
1
1
2
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
π |
π |
|||
π |
π |
x |
|
||||||
|
|
||||||||
2 |
2 |
|
|
|
|
||||
|
|
|
|
|
|
||||
Пример 2.
Непрерывная случайная величина Х задана плотностью вероятности
f x |
2 |
|
|
|
|
sin 3x, на 0; |
|
. Вне этого интервала равна нулю. Найти вероятность того, |
|
|
||||
|
3 |
|
3 |
|
что Х примет значение, принадлежащее
6
4
.
Решение.
Используем свойство
|
|
|
|
4 |
2 |
|
|
P a X b |
sin3xdx |
||
3 |
|||
|
|
||
|
|
||
6 |
|
|
P
|
|
|
b |
|
|
|
|
|
|
|
|
a X b f(x)dx |
|
|
|
|
|
||||||
|
|
|
a |
|
|
|
|
|
|
|
|
2 |
|
1 |
cos 3x |
|
|
2 |
|
3 |
|
|
|
|
|
|
cos |
||||||||
|
|
4 |
|
cos |
|
|
|
||||
3 |
|
3 |
|
|
|
9 |
|
4 |
|
2 |
|
|
|
6 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
Пример 3.
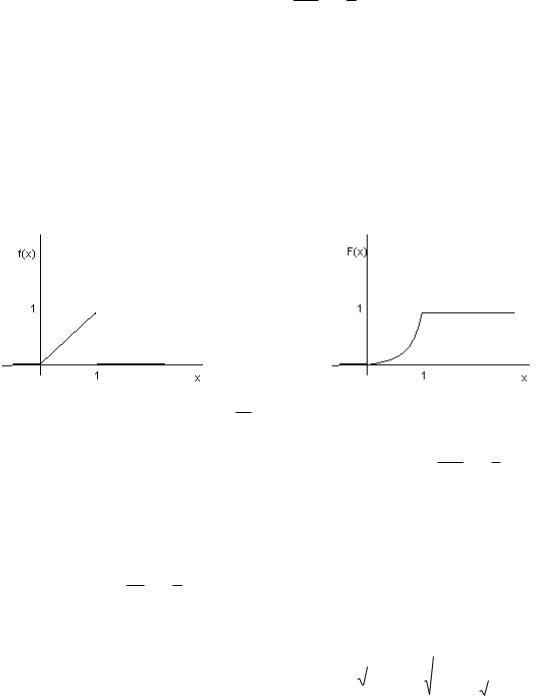
Случайная величина имеет плотность распределения ax, при 0≤х≤1
f(x)={
0, при х>1 или х<0
Требуется а) найти постоянную а
б) найти функцию распределения F(x) в) построить графики f(x) и F(x)
г) найти Р(0<х<1/4)
д) найти параметры распределения
Решение:
|
2 |
|
|
2 |
0 |
|
|
2 |
|
|
|
|
|
||||
|
9 |
|
|
2 |
|
|
|
9 |
|
|
|
|
|
|
а) используем свойство плотности распределения
|
|
0 |
|
1 |
|
|
|
1 |
|
ax |
2 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|||
f (x)dx |
0dx |
axdx |
0dx |
axdx |
2 |
|0 |
2 |
а=1, |
||||||
|
|
|
|
|
||||||||||
|
|
|
0 |
|
1 |
|
0 |
|
|
|
||||
|
|
|
|
|
|
|
|
|||||||
следовательно а=2.
|
|
|
f (x)dx |
|
|
1
.
б) при х≤0
при 0<х≤1
при х>1
F(х)=
F(x)=
F(x)=
х |
|
|
|
0dt 0 |
|
||
|
|
|
|
0 |
x |
|
|
0dt |
2tdt x |
2 |
|
|
|||
|
0 |
|
|
0 |
1 |
|
|
0dt 2tdt 0dt 1 |
|||
|
0 |
1 |
|
в)
|
1 / 4 |
|
|
|
|
1 |
|
г) Р(0<х<1/4)= |
|
2хdx x |
|
|0 |
|
|
|
|
|
|
2 |
1/ 4 |
|
|
|
|
0 |
|
|
|
|
16 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
д) математическое ожидание М(Х)= |
|
||||||
|
|||||||
|
|
|
|
|
|
|
a |
дисперсию найдем по формуле D(X)=
|
1 |
|
|
|
2x |
3 |
|
2 |
хf (x)dx = |
|
|
2 |
dx |
1 |
|
||
2х |
|
3 |
|0 |
3 |
||||
|
|
|||||||
|
0 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
М(Х2) - М2(Х), для этого в начале
вычислим М(Х2) = |
|
|
|
|
|
f x dx . |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
x |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2 |
1 |
|
|
x |
4 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
М(Х )= |
2х dx |
|
2 |
|
|0 |
2 |
, подставим в формулу дисперсии это значение: |
||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D(X)= М(Х2) - М2(Х)= |
1 |
|
4 |
|
|
1 |
. |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
9 |
|
18 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
. |
Среднее квадратическое отклонение: ( Х ) |
D( X ) |
|
|
|
|||||||||||||||||||||||
18 |
|
|
|
|
|||||||||||||||||||||||
|
3 |
2 |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Пример 4.
Математическое ожидание нормально распределенной случайной величины Х равно μ = 4 и среднее квадратическое отклонение σ = 1. Написать плотность вероятности Х.
Решение.
Для решения этой задачи просто требуется подставить значения математического ожидания μ и среднего квадратического отклонения σ в
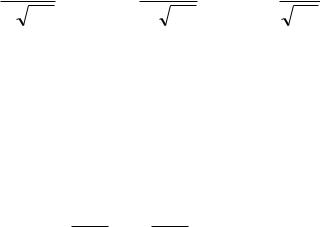
формулу функции плотности вероятности:
x |
x 4 |
|
2 |
|
2 |
f (x) |
|
1 |
|
2 |
2 |
|
|
1 |
|
2 |
|
1 |
|
|
e |
|
|
|
e |
2 1 |
|
||||
|
2 |
|
|
|
2 |
|
2 |
|||||
|
|
|
|
1 |
|
|
|
x 4 |
|
|
2 |
e |
2 |
|
.
Пример 5.
Математическое ожидание и среднее квадратическое отклонение нормально распределенной случайной величины Х соответственно равны 5 и 3. Найти вероятность того, что в результате испытания Х примет значение, заключенное в интервале (10, 16).
|
b |
a |
|
|||||
Решение. Используем формулу |
Р(a X b) Ф |
|
|
Ф |
|
|
, учитывая, |
|
|
|
|||||||
|
|
|
|
|
|
|||
что а = 10, b = 16, μ = 5, σ = 3.
16 5 |
|
10 5 |
|
Ф 3,67 Ф 1,67 |
||
Р(12 X 14) Ф |
|
|
Ф |
|
|
|
|
3 |
|
|
3 |
|
|
По таблице для значений функции Лапласа находим Ф 3,67 Ф 1,67 =0,4999 - 0,4525 = 0,0474
Контрольные задания:
1) Дана функция распределения непрерывной случайной величины Х
|
0 |
F ( X ) |
|
sinx |
|
|
|
|
|
|
1 |
|
|
при x 0, при 0 x при x /2
/2,
. Найти плотность распределения f (x).
2) |
Дана функция распределения непрерывной случайной |
величины Х |
|
0
F ( X ) sin2x
1
3)
величины
при x 0,
при 0 x /4, . Найти плотность распределения f (x).
при x /4
Для функции распределения непрерывной случайной
0 при x 0,
F ( X ) ax 2 при 0 x 2,
1 при x 2
найти коэффициент а и плотность вероятности случайной величины Х в интервал (0; 1).
4) Задана плотность распределения непрерывной случайной величины Х:
0 |
при |
x 0, |
|
|
|
|
0 x / 2, . Найти функцию распределения F(x). |
f (x) cosx при |
|||
0 |
при |
|
x / 2 |
|
|
|
|
