6 _случайные величины
.pdfМетодические рекомендации для студентов 1 курса факультета по РИУ по специальности «лечебное дело»
по самоподготовке к практическому занятию по математике
Тема: Случайные величины. Числовые характеристики дискретной и непрерывной случайной величины. Нормальный закон распределения. Вероятность попадания нормально распределенной случайной величины в интервал.
Актуальность темы: ознакомление с основными понятиями и методами теории вероятностей и случайных величин как средств решения задач физического, химического, биологического и иного характера, встречающихся как в процессе изучения профильных дисциплин, так и в дальнейшей профессиональной деятельности
Цель занятия:
1.научиться составлять закон и функцию распределения дискретной случайной величины, строить их графики, определять числовые характеристики: математическое ожидание, дисперсию, среднее квадратическое отклонение, находить с помощью функции распределения вероятность событий.
2.научиться по функции распределения находить плотность распределения вероятностей непрерывной случайной величины и наоборот, вычислять числовые характеристики непрерывных случайных величин
3.научиться вычислять числовые характеристики нормальных случайных величин, вычислять вероятность попадания в интервал непрерывной случайной величины, распределенной по нормальному закону
План изучения темы
1.Случайные величины: дискретная и непрерывная.
2.Числовые характеристики дискретной случайной величины.
3.Закон и функция распределения дискретной случайной величины. Непрерывная случайная величина.
4.Числовые характеристики непрерывной случайной величины.
5.Плотность и функция распределения непрерывной случайной величины.
6.Основные параметры нормального распределения непрерывной случайной величины.
7.Вероятность попадания возможных значений непрерывной случайной величины, распределенной по нормальному закону в заданный интервал
Рекомендуемая литература:
Основная литература:
1.Морозов, Ю.В. Основы высшей математики и статистики: учеб. для студентов мед. и фаpмацевт. вузов и фак./Ю.В. Морозов.-
М.:Медицина, 2004.-232 с.
2.Основы высшей математики и математической статистики: учеб. для студентов мед. и фармацевт. вузов/И.В. Павлушков,
Л.В.Розовский, А.Е.Капульцевич и др.-2-е изд., испр.-М.:ГОЭТАР-
Медиа, 2006.-423 с.
Дополнительная литература:
∙Методические рекомендации к практическим занятиям по высшей математике [Электронный ресурс]: учеб.-метод. пособие для вузов/ авт.-сост. : Т.А.Новичкова; ГОУ ВПО "Курск. гос. мед. ун-т", каф. физики, информатики и математики.-Курск:КГМУ, 2009.
∙Гмурман В.Е. Теория и математическая статистика. М. «Высшая школа», изд. 5, 2004.
Вопросы для самоконтроля:
1.Что называют дискретной случайной величиной? В чем ее отличие от непрерывной случайной величины?
2.Что называют законом распределения дискретной случайной величины?
3.Задайте закон распределения дискретной случайной величины таблично, аналитически, графически.
4.Дайте понятие ряда распределения, многоугольника распределения.
5.Что такое функция распределения дискретной случайной величины?
6.Что называют математическим ожиданием дискретной случайной величины?
7.Перечислите свойства математического ожидания.
8.Что называют дисперсией дискретной случайной величины? Запишите формулу.
9.Перечислите свойства дисперсии случайной величины.
10.Что называют средним квадратическим отклонением? Запишите формулу.
11.Что такое мода дискретной случайной величины?
12.Что такое медиана дискретной случайной величины?
13.Какая дискретная величина имеет биномиальное распределение?
14.Какая случайная величина называется распределенной по закону Пуассона?
15.Понятие непрерывной случайной величины. |
|
||||
16.Интегральная |
функция распределения |
случайной величины |
|||
(определение). |
|
|
|
|
|
17.Нахождение |
вероятности попадания |
случайной |
величины в |
||
заданный интервал через функцию распределения. |
|
||||
18.Дифференциальная |
функция |
распределения. |
Вероятность |
||
попадания случайной величины в заданный интервал. Условие нормировки.
19.Числовые характеристики непрерывных случайных величин, формулы для их нахождения. Вероятностный смысл математического ожидания. Назначение дисперсии и среднего квадратичного отклонения.
20.Закон нормального распределения, кривая Гаусса.
21.Нормированное нормальное распределение. Функция распределения
нормированной нормально распределенной случайной величины. 22.Вероятность попадания нормально распределенной случайной
величины в заданный интервал. |
|
|
|
23.Нахождение вероятности попадания случайной |
величины в |
||
заданный интервал через функцию распределения. |
|
||
24.Дифференциальная |
функция |
распределения. |
Вероятность |
попадания случайной величины в заданный интервал. Условие нормировки.
25.Закон нормального распределения, кривая Гаусса.
26.Нормированное нормальное распределение. Функция распределения
нормированной нормально распределенной случайной величины. 27.Вероятность попадания нормально распределенной случайной
величины в заданный интервал.
Задания на самоподготовку:
1.Имеется десять студенческих групп, насчитывающих соответственно
12, 10, 11, 8, 12, 9, 10, 8, 10 и 11 студентов.
а) Составить закон распределения случайной величины Х, определяемой как число студентов в наугад выбранной группе.
б) построить многоугольник распределения случайной величины Х в) найти её функцию распределения F(х)
г) построить график F(х)
д) найти вероятность события Р(9<Х≤11)
е) найти М(Х), D(X), σ (X).
2. Непрерывная случайная величина задана функцией распределения
0, еслих≤1
F(x) = {а(х − 1) , если1<x≤3
1, еслих>3 Требуется а) найти постоянную а
б) найти плотность распределения f(x) в) построить графики f(x) и F(x)
г) найти Р(1,5<х<2)
д) найти параметры распределения 3. Пусть случайная величина Х имеет нормальное распределение с
математическим ожиданием µ=15 и средним квадратическим отклонением σ=1. найти интервалы для Х, если вероятность интервала | Х - µ| < ε равна
0,95.
Ориентировочные основы действий:
1.Изучить основные понятия по теме
2.Ответить на вопросы для самоконтроля
3.Проработать примеры решения задач по теме
4.Выполнить задания для самостоятельного контроля
5.Решить контрольные задания по теме
После изучения данной темы студент должен знать: понятия функции и плотности распределения вероятности случайных
величин, научиться определять числовые характеристики непрерывных случайных величин и вероятность попадания значений случайной величины в заданный интервал.
уметь: составлять закон и функцию распределения дискретной случайной величины, строить их графики, определять числовые характеристики: математическое ожидание, дисперсию, среднее квадратическое отклонение, находить с помощью функции распределения вероятность событий, определять вероятность попадания значений нормально распределенной случайной величины в заданный интервал.
Краткая теория
Величину, которая в результате испытания примет одно и только одно возможное значение (при этом заранее не известно какое именно), называют
случайной.
Случайные величины обозначают прописными буквами латинского алфавита X, YZ,…, а их вероятности соответствующими строчными буквами
x, y, z,…
Дискретной называют случайную величину, которая принимает отдельные, изолированные возможные значения с определенными вероятностями.
Непрерывной называют случайную величину, которая может принимать все значения из некоторого конечного или бесконечного промежутка.
Законом распределения ДСВ называется соответствие между её возможными значениями и их вероятностями. Закон распределения чаще всего задается в табличной форме.
Xi |
x1 |
x2 |
… |
xn |
pi |
p1 |
p2 |
… |
pn |
|
|
|
|
|
Такая таблица также называется рядом распределения.
Для наглядности закон распределения ДСВ можно изобразить графически, для чего в прямоугольной системе координат строят точки (xi,pi), а затем соединяют их отрезками прямых. Полученную фигуру называют
многоугольником распределения (графическое изображение закона распределения).
pi
p3
p1
x1 x2 x3 x4 |
x5 |
xi |
Числовые характеристики ДСВ
Закон распределения полностью характеризует случайную величину. Однако часто он неизвестен и приходится ограничиваться меньшими сведениями. Иногда даже выгоднее пользоваться числами, которые описывают случайную величину суммарно, выражая в сжатой форме наиболее существенные особенности распределения. Эти числа называют
числовыми характеристиками случайной величины.
Математическим ожиданием ДСВ X с конечным числом значений называется сумма произведений возможных ее значений на их вероятности.
n |
n |
M(X) =µ= x1p1 + x2p2 +...+ xnpn = ∑xi pi ; |
∑ pi =1 |
i=1 |
i=1 |
Свойства математического ожидания:
1.Математическое ожидание постоянной (неслучайной) величины
Сравно самой постоянной
M(C) = C.
2. Математическое ожидание алгебраической суммы нескольких случайных величин равно алгебраической сумме математических ожиданий слагаемых
M(X1 ± X2 ±...± X n) = M(X1) ± M(X2) ±…± M(X n).
3. Константу можно вынести за знак математического ожидания
M(CX)=CM(X).
4. Математическое ожидание произведения нескольких независимых случайных величин равно произведению математических ожиданий этих величин
M(X1X2...Xn) = M(X1)M(X2)...M(X)n.
Модой М0 дискретного распределения называют такое значение xm случайной величины, что предшествующее и следующее за ним значения имеют вероятности меньше P(xm).
Дисперсией ДСВ X называется математическое ожидание квадрата отклонения этой величины от ее математического ожидания.
D(X ) = σ 2 = M ((X - μ )2 )= ∑n (xi - μ )2 pi
i=1
Для вычисления дисперсии более удобна формула:
D(X) = M(X 2 )- M(X)2 , где M(X 2 )= ∑n xi2 × pi
i =1
т.е. дисперсия случайной величины равна разности между математическим ожиданием квадрата этой величины и квадратом ее математического ожидания.
Свойства дисперсии.
1.Дисперсия постоянной величины равна нулю
D(С) = 0.
2.Постоянный множитель можно выносить за знак дисперсии, предварительно возведя его в квадрат:
D(CX) = C2D(X).
3. Дисперсия суммы (разности) двух независимых случайных величин равна сумме дисперсий этих величин:
D(X±Y)=D(X)±D(Y).
Средним квадратическим отклонением случайной величины называют квадратный корень из её дисперсии.
n
σ = 
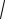D(X) = ∑(xi - μ )2 × pi
i=1
Основные законы распределения ДСВ
Биномиальное распределение
Пусть величина Х – число появлений события А в n повторных независимых испытаниях, причем для каждого испытания P(A)=p, P(Ā)=q.
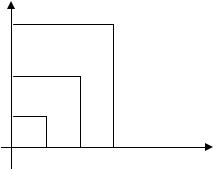
Тогда вероятности значений случайной величины Х (x0=0, x1=1, …,
x |
=n) можно определить по формуле Бернулли P |
(x)= C x p x qn−x = |
n! |
|
p x qn−x |
|
x!(n − x)! |
||||||
n |
n |
n |
|
|||
|
|
|
|
|||
|
M(X)=np |
|
|
|
|
|
|
D(X)=npq |
|
|
|
|
|
|
σ(X)=√npq |
|
|
|
|
|
Распределение Пуассона
Когда вероятность событий А много меньше единицы и число испытаний n – велико (n≥50, p≤0,1) формула Бернулли неуместна. Тогда используется формула Пуассона
P (x)≈ |
μ x |
e−μ , где μ = np |
|
||
n |
x! |
|
|
|
Распределение такой величины называется распределением Пуассона
Функцией распределения ДСВ (кумулятивной) называется функция F(X), равная вероятности события, в котором случайная величина Х приняла значение меньше х, F(X)=P(X<x).
F(X)
|
|
|
|
|
|
1 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
p1+p2 |
|
|
|
|
|
||
0, |
x < x1 |
|
|
p1 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|||||
p , |
x |
|
≤ x < x |
|
|
|
|
|
|
|
|
||
1 |
|
1 |
|
|
2 |
|
|
|
|
|
|
x |
|
F(X)= p1 + p2 , x |
2 ≤ x < x3 |
0 |
x1 x2 x3 |
||||||||||
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
... |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xn < x |
|
|
|
|
|
|
|
|
|
|||
1, |
|
|
|
|
|
|
|
|
|
||||
Функцией распределения (интегральной функцией) непрерывной случайной величины Х называется функция F(х), равна вероятности P(Х<х) того, что случайная величина приняла значение меньше х
F(х) = P(Х<х)
Свойства:
1. 0 ≤ F(X)≤1 (из определения вероятности)
2.F(х) – неубывающая функция
3.Вероятность попадания случайной величины Х в полуинтервал [a,b) равна разности между значениями функции распределения в правом и левом концах интервала (a,b)
P(a ≤ x < b) = F(b)− F(a )
4. Вероятность того, что случайная величина Х примет заранее заданное значение а равна нулю
P(X = a) = 0
5. Если возможные значения непрерывной случайной величины расположены на всей числовой оси, то
lim F(X) = 0, |
lim F(X) = 1 |
x →-∞ |
x →+∞ |
Плотностью распределения (плотностью вероятности) непрерывной случайной величины Х называют функцию f(x), равную производной её интегральной функции
f(X) = F'(X)
f(x)
a |
b |
x |
|
Свойства:
1.f(x) – функция неотрицательная, т.к. F(x) – неубывающая, то F’(x)=f(x)≥0
2.Вероятность того, что непрерывная случайная величина Х в результате испытания примет какое-нибудь значение из интервала (a,b) равна определенному интегралу плотности вероятности в пределах от a и b.
b
P(a ≤ X < b) = ∫ f(x)dx = F(b) − F(a)
a
+∞
3.∫ f(x)dx = 1 - условие нормировки плотности
-∞
вероятностей
x
4.F(X) = ∫ f(x)dx
-∞
Числовые характеристики непрерывных случайных величин
|
|
+∞ |
|
|
Математическое ожидание M ( X ) = μ = ∫ x × f (x)dx |
||||
Дисперсия |
|
−∞ |
|
|
|
|
|
|
|
+∞ |
+∞ |
+∞ |
|
+∞ |
D( X ) = σ 2 = ∫ (x - μ )2 × f (x)dx = = ∫ x2 × f (x)dx - 2μ ∫ x × f (x)dx + μ 2 ∫ f (x)dx = |
||||
−∞ |
−∞ |
−∞ |
|
−∞ |
= M (X 2 )− 2μ 2 + μ 2 = M (X 2 )− μ 2 |
|
|
|
|
Среднее квадратическое отношение σ ( X ) = |
|
|
||
D(X ) |
||||
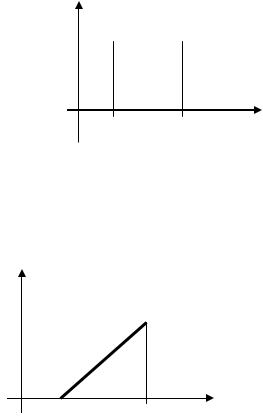
Модой М0(x) непрерывной случайной величины Х называется то её возможное значение, которому соответствует локальный максимум плотности распределения.
В частности, если распределение имеет два локальных максимума, то его называют бимодальным.
Медианой Ме(х) непрерывной случайной величины Х называют её возможное значение, которое определяется равенством.
P(X < Me (X ))= P(X > M e (X ))
Геометрически медиану можно истолковать как точку, в которой ордината f(x) делит пополам площадь, ограниченную кривой распределения.
Равномерное распределение Непрерывная случайная величина Х имеет равномерное
распределение вероятностей на отрезке [a,b], если её плотность вероятности на [a,b] постоянна, а вне интервала равна нулю, т.е.
F(X)
|
|
|
1 |
|
|
|
|
|
|
|
|
|
b-a |
|
|
||||
0, x ≤ a |
|
|
|
|
|
|
|
||
|
|
|
|
|
a |
b |
x |
||
f (x)= |
1 |
, a < x ≤ b |
|
|
|
||||
|
|
|
|
|
|
|
|
||
b − a |
|
|
|
|
|
|
|
|
|
0, x > b
Функция распределения случайной величины Х, распределенной по равномерному закону
F(x)
1 
0, x ≤ a |
|
|
|
|||||||||
|
|
|
||||||||||
|
− a |
|
|
|
|
|
|
|
||||
0 |
a |
b |
x |
|||||||||
x |
||||||||||||
F (x)= |
|
|
|
, a < x ≤ b |
|
|
|
|||||
|
− a |
|
|
|
||||||||
b |
|
|
|
|
|
|
|
|||||
1, x > b |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|||
M (x)= |
a +b |
, D(x)= |
(b − a)2 |
|
|
|
|
|
||||
|
|
|
|
|
||||||||
2 |
|
12 |
|
|
|
|
|
|||||
Вероятность попадания величины Х, распределенной по равномерному закону на [a,b] в интервал (х1, х2) равна
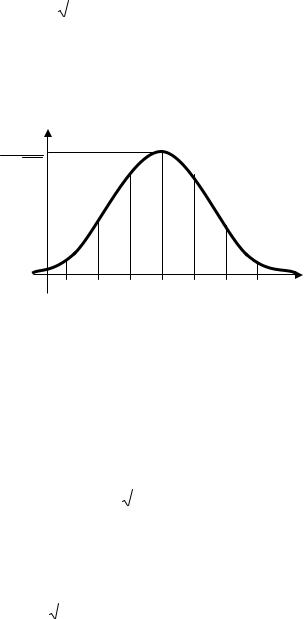
x2 |
|
x2 − x1 |
|
P(x1 < x < x2 ) = ∫ |
f (x)dx = |
||
b − a |
|||
x1 |
|
||
|
|
Нормальный закон распределения (закон Гаусса)
Закон распределения вероятностей непрерывной случайной величины Х называют нормальным, если плотность вероятности определяется формулой
f (x) = |
|
1 |
|
− |
(x− μ )2 |
|
|
|
|
e 2σ 2 , где µ – мат. ожидание сл.вел. Х, σ – ср.кв. |
|||||
|
|
|
|
||||
σ |
|
2π |
|||||
|
|
|
|
|
|
||
отклонение сл.вел. Х.
График функции y=f(x) называют нормальной кривой распределения
или кривой Гаусса.
f(x)
1
σ 
2π
µ-3σ |
µ |
µ+3σ x |
Площадь фигуры, ограниченной кривой Гаусса и двумя прямыми х = а и х = b, где a<b, представляет собой вероятность того, что сл.вел. Х лежит
b
между а и b, т.е. P(a ≤ X < b) = ∫ f(x)dx
a
Нормальное распределение с параметрами µ=0, σ=1 называют
нормированным или стандартным.
Функция ϕ (x) = |
|
1 |
|
− |
x 2 |
|
|
|
|
|
e 2 называется плотностью вероятности |
||||
|
|
|
|||||
2π |
|||||||
|
|
|
|
|
|
||
нормированного (стандартного) распределения.
Функция распределения стандартного распределения есть
|
|
|
x |
x 2 |
|
Ф(x) = |
|
1 |
∫ e− |
|
dx − функция Лапласа |
|
2 |
||||
|
|
||||
|
|
2π −∞ |
|
|
|
Вероятность попадания в заданный интервал нормальной случайной величины