7 _статистические оценки

Методические рекомендации для студентов 1 курса факультета по РИУ по специальности «лечебное дело»

по самоподготовке к практическому занятию по математике

Тема: Статистическое распределение выборки, дискретные и интервальные вариационные ряды. Точечные и интервальные оценки параметров распределения. Погрешности измерений и их оценки.

Актуальность темы: ознакомление с основными понятиями и методами математической статистики как средством решения задач физического, химического, биологического и иного характера, встречающихся как в процессе изучения профильных дисциплин, так и в дальнейшей профессиональной деятельности

Цель занятия: научиться строить статистические ряды для дискретных и непрерывных случайных величин и вычислять точечные оценки генеральных параметров, вычислять погрешности при прямых и косвенных измерениях.

План изучения темы

1.Основные задачи математической статистики.

2.Генеральная и выборочная совокупности.

3.Дискретный вариационный ряд и его графическое изображение.

4.Интервальный вариационный ряд и его графическое изображение. Виды статистических оценок.

5.Требования к статистическим оценкам.

6.Понятия генеральной и выборочной средних.

7.Понятия генеральной, выборочной и исправленной дисперсий.

8.Понятия генерального, выборочного и исправленного среднего квадратического отклонения.

Рекомендуемая литература:

Основная литература:

1.Морозов, Ю.В. Основы высшей математики и статистики: учеб. для студентов мед. и фаpмацевт. вузов и фак./Ю.В. Морозов.-

М.:Медицина, 2004.-232 с.

2.Основы высшей математики и математической статистики: учеб. для студентов мед. и фармацевт. вузов/И.В. Павлушков, Л.В.Розовский, А.Е.Капульцевич и др.-2-е изд., испр.-М.:ГОЭТАР-

Медиа, 2006.-423 с.

Дополнительная литература:

∙Методические рекомендации к практическим занятиям по высшей математике [Электронный ресурс]: учеб.-метод. пособие для вузов/ авт.-сост. : Т.А.Новичкова; ГОУ ВПО "Курск. гос. мед. ун-т", каф. физики, информатики и математики.-Курск:КГМУ, 2009.

∙Гмурман В.Е. Теория и математическая статистика. М. «Высшая школа», изд. 5, 2004.

Вопросы для самоконтроля:

1)Определение статистического ряда.

2)Определение генеральной совокупности.

3)Определение выборочной совокупности.

4)Репрезентативность выборки.

5)Виды выборок.

6)Что называется вариантой?

7)Определение ранжирования.

8)Определение частоты, относительной частоты, накопленной частоты.

9)Алгоритм построения интервального вариационного ряда.

10)Определение полигона, кумуляты (дискретного вариационного ряда).

11)Определение гистограммы, кумуляты (интервального вариационного ряда) определение статистической оценки.

12)какие требования предъявляются к статистическим оценкам.

13)Какая статистическая оценка называется смещенной, несмещенной?

14)формулы для расчета генеральной и выборочной средней для сгруппированных и несгруппированных данных.

15)формулы для расчета генеральной и выборочной дисперсии для сгруппированных и несгруппированных данных.

16)Какой оценкой считается выборочная средняя для генеральной средней?

17)Какой оценкой считается выборочная дисперсия для генеральной?

18)Формула для расчета исправленного среднего квадратического отклонения.

19)Какие измерения называются прямыми?

20)Что понимают под истинной абсолютной погрешностью величины X?

21)Что принимают за истинное значение величины X?

22)Что служит точечной оценкой истинного значения величины X?

23)Что служит оценкой дисперсии X?

24)Как рассчитать абсолютную погрешность среднего арифметического?

25)Как найти границы доверительного интервала для истинного значения величины X ?

26)Какие измерения называются косвенными?

27)Если y = f(x1, x2, ..., xn), то по какой формуле вычисляется средняя квадратическая погрешность среднего значения y?

28)По какой формуле находится абсолютная погрешность y: у ?

29)Как найти относительную погрешность y: ε у ?

Задания на самоподготовку:

1. В результате отдельных испытаний активности тетрациклина были получены следующие значения (в единицах действия на 1 мг): 925, 940, 760, 905, 995, 965, 940, 925, 940, 905. составить ряда распределения. Построить полигон, кумуляту.

2.Построить гистограмму относительных частот по распределению выборки: 11, 15, 16, 18, 15.5, 19, 20.1, 20.9, 23, 24.5, 23, 21, 23.9, 24.6, 25.5, 26, 29, 28.6, 30.1, 32.

3.Найти исправленное среднее квадратическое отклонение по данному распределению выборки

Ориентировочные основы действий:

1.Изучить основные понятия по теме

2.Ответить на вопросы для самоконтроля

3.Проработать примеры решения задач по теме

4.Выполнить задания для самостоятельного контроля

5.Решить контрольные задания по теме

После изучения данной темы студент должен знать: понятие вариационного ряда, его виды и их графическое изображение,

понятия статистической оценки, их виды, требования к оценкам, понятия генеральной и выборочной средней, генеральной и выборочной дисперсий. уметь: строить статистические ряды для дискретных и непрерывных случайных величин и вычислять точечные оценки генеральных параметров, вычислять погрешности при прямых и косвенных измерениях.

Краткая теория

Математическая статистика – это раздел прикладной математики, посвящённый методам сбора, группировки и анализа статистических сведений, полученных в результате наблюдений или экспериментов.

Отсюда следуют задачи математической статистики:

способы отбора статистических данных.

способы группировки статистических данных.

методы анализа данных:

∙оценка параметров известного распределения;

∙оценка неизвестной функции распределения;

∙оценка зависимости одной случайной величины от других;

∙проверка статистических гипотез.

способы определения числа наблюдений (планирование эксперимента).

принятие решений.

Вматематической статистике изучение случайной величины связано

свыполнением ряда независимых опытов, в которых она принимает определенные значения.

Статистическая совокупность – множество объектов, однородных относительно некоторого качественного или количественного признака.

Н-р, если имеется серия таблеток лекарственного вещества, то качественным признаком может служить стандартность таблетки, а количественным – контролируемая масса таблетки.

Генеральная совокупность – совокупность, состоящая из всех объектов, которые могут быть к ней отнесены.

Теоретически это м.б. бесконечно большая или приближающаяся к бесконечности совокупность.

Н-р, все больные ревматизмом на земном шаре – генеральная совокупность. Реально это в конкретных пределах (город, область).

Число объектов генеральной совокупности называют её объемом и обозначают N.

Выборочная совокупность – множество объектов, случайно отобранных из генеральной совокупности.

Число объектов в выборке называют её объемом и обозначают n.

Для того, чтобы свойства выборки достаточно хорошо отражали свойства генеральной совокупности выборка должна быть репрезентативной (представительной).

Это требование обеспечивает случайность отбора элементов в выборку, т.е. равновероятность попасть в выборку любому объекту.

В зависимости от техники отбора объектов из генеральной совокупности выборки делятся на:

Выборки

На практике пользуются бесповторной выборкой.

При больших объемах N генеральной совокупности и малом относительном объеме n/N выборки различия в формулах, описывающих обе выборки по технике их отбора невелики.

Дискретный ряд распределения

Наблюдаемые значения признака называются вариантами. Ранжирование – расположение вариант по возрастанию, либо

убыванию.

Вариационным рядом называется ранжированный ряд вариантов и соответствующих им частот.

Статистическим распределением выборки называют перечень вариант и соответствующих им частот или относительных частот.

Пусть из генеральной совокупности извлечена выборка объемом n. Количественное значение изучаемого признака x1 появилось m1 раз, x2 – m 2

раз, …, x k – m k раз.

k

Причем ∑mi = n

i =1

Числа mi называют частотами, а их отношения к объему выборки n – относительными частотами pi=mi/n. Причем Σpi=1.

Для случая когда количественный признак является дискретным, его значения и соответствующие им частоты или относительные частоты представляют виде таблицы.

Таблицу, содержащую значения вариант признака и их частоты или относительные частоты, называют статистическим дискретным рядом распределения. Статистическим распределением выборки называется сам набор вариант и соответствующий им частот или относительных частот

При изучении вариационных рядов наряду с понятием частоты используется накопленная частота (mi*). Накопленная частота показывает, сколько наблюдалось вариантов со значением признака меньше х.

Отношение наколенной частоты mi* к общему числу наблюдений n называется относительной частотой pi*= mi*/n.

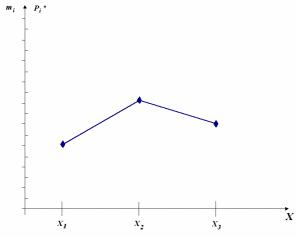
Графическое изображение дискретного статистического ряда – полигон частот (относительных).

Полигон служит для изображения дискретного вариационного ряда и представляет собой ломаную, в которой концы отрезков прямой имеют координаты (xi, mi) или (xi, pi) в случае полигона относительных частот.

Интервальный статистический ряд.

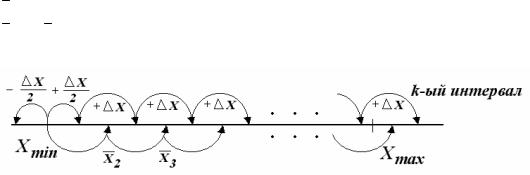
В случае большого количества вариант (n>50) и непрерывного распределения признака статистическое распределение признака можно задать виде последовательности интервалов и соответствующих им частот.

Чаще используют равноинтервальный ряд.

Нужно правильно выбрать ширину классового интервала. Число интервалов должно зависеть от размаха выборки и её объёма.

Алгоритм построения гистограммы.

1.Дана выборка Х = {x1, x2, …, x n}; n – её объём

Размах выборки D = xmax – x min

2.Число классов

К= 1 + 3,32 × lg n (формула Стерджесса для n < 100)

К= 5 × lg n (формула Брукса для n > 100)

3. Величина классового интервала Dx = D / К

4.Границы и середины частичных интервалов

x1л = xmin – Dx / 2

x1пр = x2л = xmin + Dx / 2

х1 = xmin

х2 = х 1 + Dx

5.Частоты попадания в интервал:

вариационных рядов и представляет собой ступенчатую фигуру из прямоугольников с основаниями, равными интервалам значений признака xi=xi+1-xi, i=1,2,…,k и высотами, равными частотам (относительным частотам) mi (pi) интервалов.

Если соединить середины верхних оснований прямоугольников отрезками прямой, то можно получить полигон того же распределения.

Эмпирическая функции распределения Чтобы получить представление о распределении случайной

величины Х, для которой неизвестен закон распределения, строят эмпирическую функцию распределения.

Эмпирической функцией распределения (функцией распределения выборки) называют функцию F*(x), определяющую для каждого значения х относительную частоту события X<xi.

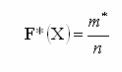, где m* - число наблюдений, при которых наблюдалось значение признака Х меньше х.

Функцию распределения генеральной совокупности называют теоретической функцией.

Различие между эмпирической и теоретической функциями в том, что теоретическая функция определяет вероятность события Х<х, а эмпирическая – относительную частоту данного события.

Понятие статистической оценки.

Требуется изучить количественный признак генеральной совокупности. Допустим, нам известен закон распределения генеральной совокупности. Этот закон определяется несколькими параметрами. Для оценки неизвестных параметров генеральной совокупности используются данные выборки.

Статистической оценкой неизвестного параметра распределения генеральной совокупности называют функцию от наблюдаемых случайных величин.

Обозначим:

θ – неизвестный параметр; θ* – статистическая оценка неизвестного параметра; θ* = f (x1, x2, …, x n)

Статистическая оценка θ* является случайной величиной, поэтому имеет дисперсию и среднеквадратическое отклонение, а также ошибку репрезентативности (отклонение выборочного показателя от генерального).

Статистические оценки бывают двух видов: точечные и интервальные.

Оценка одним числом, зависящим от выборочных данных, называется точечной.

Оценка двумя числами, являющимися концами интервала, называется интервальной.

Точность, надежность оценки

Интервальной оценкой называют оценку, которая определяется двумя числами – концами интервала.

Интервальные оценки позволяют установить точность и надёжность точечной оценки.

Пусть q* – точечная оценка неизвестного параметра q, являющаяся случайной величиной.

Чем меньше ½q - q*½, тем точнее q* определяет параметр q.

Если δ > 0 и ½q - q*½ < δ, то чем меньше δ, тем точнее оценка. Число

δназывается точностью оценки.

Всилу случайности q* можно лишь говорить о вероятности осуществления неравенства ½q - q*½ < e.

Надёжностью (доверительной вероятностью) оценки q* называют вероятность g, с которой осуществляется неравенство ½q - q*½ < δ.

Обычно g = 0,95; 0,99; 0,999… P(|Θ-Θ*|< δ)=γ

Иногда говорят, что доверительная вероятность g характеризует степень нашей уверенности в том, что доверительный интервал покроет параметр q.

Р{q* - e < q < q* + e} = g означает, что вероятность того, что интервал (q* - e; q* + e) заключает в себе неизвестный параметр q, равна g:

Вероятность того, что неизвестный параметр не попадёт в интервал ½q - q*½ < e, равна 1 - g = a (уровень значимости).

Уровнем значимости (риском) называют вероятность того, что модуль отклонения эмпирической характеристики от теоретической превысит предельную ошибку P(|Θ-Θ*|< ∆)=γ, предельная ошибка – максимально допустимая |Θ-Θ*|< ∆

Распределение Стьюдента

Пусть X ~ N(µ,σ), причем параметры распределения неизвестны.

Рассмотрим распределение величины T = xв − μ .

Sx

Распределение величины Т с f=n-1 степенями свободы называется t- распределением или распределением Стьюдента.

Функция плотности вероятности φ(t) зависит от числа степеней свободы и не зависит от дисперсии случайных величин.

С ростом числа степеней свободы распределение данной величины приближается к нормальному

Интервальной оценкой математического ожидания при неизвестной дисперсии является интервал

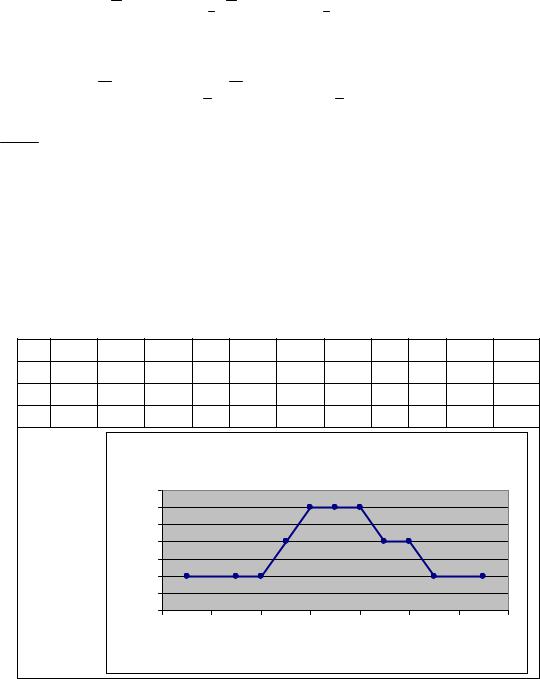
(x - tγ ( f )× Sx ; x + tγ ( f )× Sx )

Интервальной оценкой математического ожидания при известной

дисперсии является интервал

(x -uα × Sx ; x + uα × Sx )

Ф(uα ) = 1− α - функция Лапласа.

2

Примеры решения задач

1)Представить в виде статистического дискретного ряда, построить полигон частот, относительных частот, кумулятивную кривую (кривую накопленных частот): 6,7; 6,8; 7; 6,5; 7,3; 7; 7,2; 6,9; 7,1; 6,8; 7,1; 6,8; 7,1; 7,2; 6,8; 6,9;

7; 6,7; 6,6; 6,3; 7,5; 6,9.

Решение. mi – частота, p – относительная частота, pi* - накопленная относительная частота

.