5.4. Connecting capacitors

There are parallel and serial connection.

In a parallel connection of capacitors are connected with similarly charged plates. Then the total charge of capacitors equals:

Q = Q1 + Q2 + Q3

Q₁=U_ABC₁,

Q₂=U_ABC₂ ,

Q₃=U_ABC₃..

Тоді Q_заг=U_AB (C₁ + C₂ + C₃)

The capacity of this battery:

C₁

C₂

C₃

C_n

u

fig.5.9

In a parallel connection of capacitors battery capacity is the sum of the capacities enabled:

In a serial connection capacitors are connected with oppositely charged plates.

Total battery: Q = Q1 = Q2 = Q3.

The voltage between points A and B:

U = U1 + U2 + U3

C₁ C₂ C₃ C_n

U

fig.5.10

In a series connection battery capacity is given by:

;

 

Lecture 6

Paragraph 4. Energy electrostatic field

§6. Energy of the electrostatic field

6.1. The energy of point charges

Consider a system of two point charges. Find the algebraic sum of elementary operations of the forces F1 and F2, which interact charges. Let the reference frame K during Δt charges movedandand then work of the force, is numerically equal to

Given that the force , according to Newton's third law, the expression for work can be rewritten as:

The value in brackets is the movement of the charge 1 with respect to the charge 2 in the system K ', which is tightly connected with the charge 2 and is moving along with him steadily torwards the system K.

The movement of the charge l in the system K can be represented as a movementof the system K '.

K K’ 

         z z’  

1 2

dl₁ dl₂

x(x’)

y y

fig.6.1

Then:

From this expression we see that the sum of elementary operations in an arbitrary reference frame K is always equel to the unit work carried out by the force action on one charge in the frame, where another charge is at rest. That is, work δА ₁₂ does not depend on the choice of the K-th frame of reference.

Force F₁, acting on a charge of 1 by charge 2 is conservative that is why the work force on moving dl₁ can be presented as a reduction in the potential energy of charge was in charge 1 in the field of charge, 2 or as a reduction in the potential energy of interaction between the considered pairs of charges. That is . Potential energyW₁₂ depends only on the distance between the charges.

Let’s look the system of three charges. The work performed by all the forces of interaction when moving all charges can be represented as a sum of elementary operations of the three pairs of interactions.

However, for each pair of interactions . And so elementary work:

where W - the total energy of interaction of charges. Each summand depends on the distance between the respective charges and therefore the potential energy of interaction is a function of configuration of the charge system. Similar considerations are specific to systems with any number of charges.

So each configuration of any system of charges has a value of energy and work of all the forces of interaction by changing the configuration is numerically equal to the decrease in potential energy.

. (6.1)

We find an expression for the potential energy W. For this we consider a system of three point charges.

Convert this amount as follows:

(as Wik = Wki).

                           

Then the total energy of interaction rewritten as:

Group the summands with the same first index:

Each amount in round parentheses is the energy of interactionof the charge with two other charges. Therefore, the last expression can be written as the sum

.

Generalization to a system with an arbitrary number of charges is apparent. It is clear that in the calculations and considerations the expression does not depend on the number of charges. Therefore, the interaction energy of charges in the general case:

 . (6.2)

Given that the definition of potential energy potential is numerically equal to the product of the charge on the potential field in which it is found:

,

where Qi –i-th charge of a system, φi - potential created at the location of the i-th charge by all other charges of a system. Substitute this expression into the formula (6.2) and obtain the final expression for the energy of interaction of point charges.

 . (6.3)

If the charges are distributed continuously, by resolving the the system of charges on a set system of elementary charges and going from summation to integration in (6.3) we find that

(6.4)

where φ - potential created all charges in the system of volume element dV. A similar expression can be written in the resolution of charges on the surface:

.

You may mistakenly assume that equation (6.4) - is just a modified equation (6.3) which corresponds to the replacement representation of point charges representing by representation of continuous distribution charges. In fact, these expressions differ in meaning. The divergence lies in different meanings at potential φ.

Let the system consists of two balls that have charges Q1 i Q2. The distance between the balls is much larger than the balls themselves, so the charges Q1 i Q2 can be considered a point. Let’s find the energy system using both formulas, then

,

where φ12 - potential created by the second charge at the location of the first one. Similar content has the potential φ21.

According to formula (6.4) we have to charge to break into infinitely small size ρdV charges and each of the elements multiplied by the potential created not only by other balls, but also by elements of the balls and, so, the result will be different.

,

where W1 – the energy of interaction of the elements of the charge of the first ball, W2 – the energy of interaction of the elements of the charge of the first ball, W12 -the energy of interaction of the elements of the charge of the first ball with the elements of the charge of the second ball.

Energy W1, W2 are called self-energy charges Q1 and Q2 respectively, W12 - interaction energy charges Q1 and Q2.

Thus, the calculation of the energy equation (6.3) gives only the value of W12, and with the formula (6.4) have a total energy of interaction (with its own energy charges).

Using formula (6.4) we can be obtain energy of charged conductor and capacitor.

6.2. Energy isolated charged conductor

Let the conductor has a charge Q and the potential φ, since the value of the potential at all points where the placed is the same, it can be taken outside the integral and then the integral value will only include the charge on a conductor (see. formula (4)). And given that .

 . (6.6)

6.3. The energy of a charged capacitor

Let Q and φ are charge and potential of the positively charged plate of the capacitor. According to (6.4) potential energy can be divided into two parts for two plates:

.

Since Q + = - Q-, then

,

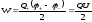U = Δφ is potential difference on capacitor plates.

. (6.7)

These formulas determine the total energy of interaction.

Formula (6.6) and (6.7) is also valid in the presence of the dielectric.

6.4. The energy of electrostatic field

Equation (6.4) defines the electrical energy of any system by the charge and potential total energy can also be expressed in terms of the electric field intensity.

Consider a flat capacitor, disregarding changes in the field at the edges of the plates (ie neglecting edge effects). The energy of the capacitor is determined by formula (6.7).

Substituting this expression for the capacitor plate of the capacitor flat: :

Because the relationship is the electric field, and the product - the amount of space between between capacitor plates, finally, we have:

 . (6.8)

The formula is valid for isotropic a homogeneous field that fills the volume V.

If dielectric, given that D = εε0E, can also be written:

. (6.9)

Integrand has the energy content of the field,which is located in the volume dV, which leads to the idea of localization in the energy field. From the last two equations it follows that electricity distributed in space with some volumetric energy density ω.

 . (6.10)

The last formula is valid only for the isotropic dielectric for which the relation between polarization and intensity of the external field

.

Lecture 7

Chapter 5. Direct electric current