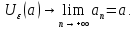ekzamen_шпора
.docx|
1. Відображення множин. Поняття образу та прообразу. Композиція відображень. |
|
Нехай Х,У деякі множини Озн:Відображенням множини Х в множину У назив. правило f за яким кожному елементу множини Х ставиться у відповідність єдиний елемент У: F:xy Озн:Якщо Х,У – числові множини, то це функція. Озн:Якщо для а є А і b є B при відображенні f:А->B має місце b=f(а), то елемент b називається образом елемента а. Елемент а – прообраз b. Види відображень:інєкція,сурєкція,бієкція. Якщо
f:Х—>У,g:Y—>Z
то можна побудувати композицію цих
відображ. g |
|
Складена функція: властивості |
|
Навіть
якщо визначені обидві композиції f |
|
Асоціативність
має місце, тобто якщо f:Х—Y,
g:Y—Z,
х:Z—B,
то
х |
|
|
|
2. Аксіоматичне визначення множини дійсних чисел. |
|
Озн:Множина R назив множиною дійсних чисел а її елементи дійсними числами, якщо виконані наступні аксіоми: |
|
a,b є R: , a+b=b+a , a+(b+c)=(a+b)+c , a+0=a , a+(-a)=0 a*b=b*a , a*(b*c)=(a*b)*c , a*1=a , a*a^-1=1 , a*(b+c)=ab+ac 1!=0 . a<=a , a<=b and b<=a a=b , a<=b and b<=c a<=c a<=b or b<=a , a<=b a+c<=b+c , 0<=a and 0<=b 0<=a*b |
|
3.Індуктивні множини. Метод математичної індукції. |
|
Озн:Індуктивна
множина- числова множина А назив.
індуктивною,якшо для
Приклад: R,Q; |
|
Т: якщо А та В – індукт множини то С=А перетин В теж індукт;
|
|
Озн:Множина натур. Чисел назив. Перетин всіх індуктивних числових множин, що містять число 1. |
|
ММІ: Якщо деяке твердження дельта справедливе для n=1 З припущення, що воно справедливе для n=k випливає його справедливість для n=k+1 Випливає, шо твердження справедливе для всіх натуральних чисел. |
|
4. Полярна система координат. |
|
Озн:Полярна система координат — двовимірна система координат, в якій кожна точка на площині визначається двома числами — кутом та відстанню. Полярна система координат особливо корисна у випадках, коли відношення між точками найпростіше зобразити у вигляді відстаней та кутів; в поширенішій, Декартовій, або прямокутній системі координат, такі відношення можна встановити лише шляхом застосування тригонометричних рівнянь. |
|
Полярна система координат задається променем, який називають нульовим або полярною віссю. Точка, з якої виходить цей промінь називається початком координат або полюсом. Будь-яка інша точка на площині визначається двома полярними координатами: радіальною та кутовою. Радіальна координата (зазвичай позначається r) відповідає відстані від точки до початку координат. Кутова координата, що також зветься полярним кутом або азимутом і позначається φ, дорівнює куту, на який потрібно повернути проти годинникової стрілки полярну вісь для того, щоб потрапити в цю точку. Визначена таким чином радіальна координата може приймати значення від нуля до нескінченості, а кутова координата змінюється в межах від 0° до 360°. Однак, для зручності область значень полярної координати можна розширити за межі повного кута, а також дозволити їй приймати від'ємні значення, що відповідатиме повороту полярної осі за годинниковою стрілкою. Пару полярних координат r та φ можна перевести в Декартові координати x та y шляхом застосування тригонометричних фукнцій синуса та косинуса: |
|
x = r cos φ , x = r sin φ в той час як дві Декартові координати x та y можуть бути переведені в полярну координату r: r2 = x2 + y2 (за теоремою Піфагора). Для визначення кутової координати φ, слід взяти до уваги два такі міркування: Для r = 0, φ може бути довільним дійсним числом. Для r ≠ 0, аби отримати унікальне значення φ, слід обмежитись інтервалом в 2π. Зазвичай, обирають інтервал [0, 2π) або (−π, π]. |
|
5. Комплексні числа, різні форми запису, арифметичні операції з комплексними числами |
|
Озн:Вираз виду x+iy, де x,y – дійсні числа, а i – символ для якого i2 =-1 назив. комплексним числом. Х-ReZдійсні числа компл. Числа Z Y=ImZ уявна частина компл. Числа Z |
|
Арифметичні
дії виконуються аналогічно до дій з
многочленами, але з урахуванням
рівності
Z1+Z2=(a+c)+i(b+d); Z1*Z2=(a+bi)(c+di) Z1/Z2=a+bi/c+di=(a+bi)(c-di)/(c+di)(c-di) Z1-Z2=a+bi-c-di Дійсні числа – це комплексні, де уявна частина = 0. |
|
Озн:Два компл числа назив. однаковими якщо уявні і дійсні частини однакові. Компл. Число може бути представлене у тригоном формі:
Або у формі Ейлера:
|
|
6.Тригонометрична форма комплексного числа. Формулa Муавра, корені з комплексних чисел. |
|
Щоб представити число у тригоном формі, досить записати модуль і помножити його таким чином:
Маємо
Добуток та частка компл. Чисел в тригоном. Формі: |
|
Доводиться
просто за формулами тригоном. Суми.
Розкриваючи дужки:
|
|
аналогічно для формули Ейлера:
|
|
Формула Муавра:
|
|
Озн:
Корінь
з компл. Числа: Число W
назив. Коренем н-порядку з компл. Числа
Z,
якщо
|
|
Отже:
|
|
7.Обмежені множини. Точна верхня та нижня межі. |
|
Озн:
Множина
А назив. Обмеженою зверху, якщо
Озн:
Нехай
А
Озн: Якщо А обмежена знизу, тоді найбільша з її верхнуї меж назив. точною нижньою межою і позначається infA. Для необмежених зверху і знизу множин інфінум і супремум дорівнюють +-нескінченність. |
|
Т:
Всяка обмежена зверху множина має
супремум А, знизу – інфінум.Нехай
А – обмежена зверху. Множина B
всіх її верхніх меж теж непуста, при
чому для будь якого b З визначення супремемуму: Якщо S=supA, то: 1)
2)
|
|
8.Лема про вкладені відрізки (принцип Коші-Кантора). |
|
Озн: Функція, що відображає множину натуральних чисел в множину Х, назив. послідовністю елементів множини Х. Озн: формула за якою, за номером можна обчислити його значення називається загальним членом послідовності. Озн:
Вкладена множина: нехай х1,х2,х3…хN
– послідовність
деяких множин, для яких має місце
|
|
Принцип
Коші-Кантора:
Для кожної послідовності вкладених
відрізків існує спільна точка С. Якщо
крім цього в послідовності для
позначимо
відрізок
З
умови випливає
що для будь якого m,n
Від супротивного: Припустимо
Тобто не мають спільних точок, що суперечить умові. Існування спільної точки показуємо за аксіомою повноти. Єдиність: припустимо що таких точок дві. Вони не рівні між собою. Нехай для визначеності c1<c2 Тоді для всіх номерів н: aN<=c1<c2<=bn=>aN-bN=c2-c1 Маємо протиріччя. |
|
9.Принцип Бореля-Лебега (про скінченне підпокриття). |
|
Озн:
Нехай А – деяка множина елементів а.
Нехай
кожному елементу а відповідає деяка
множина Ха. Кажуть, що множина множин
Ха покриває множину B,
якщо
Озн:Якщо деяка множина Ха повністю покриває B, то це підпокриття множини B |
|
Лема Бореля-Лебега: в усякій системі інтервалів S={I}, що покривають відрізок I=[a;b] можна виділити скінчене підпокриття. Від супротивного припустимо, що є система інтервалів, де не можна виділити скінчене підпокриття позначимо I1=[a;b] поділимо навпіл цей интервал. Тоді хоча б для однієї з половинок теж не можна виділити скінченого підпокриття. Позначимо половинку I2 і знову поділимо навпіл. Ділимо так Н разів. Отримуємо: I1 підмнож I2 підмнож I3 підмнож … In. Отримали послідовність вкладених відрізків для кожного з яких не можна виділити скінченого під покриття. При
чому довжина In=b-a/ Позначимо
E={c-a В
множині {In}
c
є In* => In* є
Маємо протиріччя. |
|
10. Принцип Больцано–Вейєрштраса (про граничну точку). |
|
Озн: точка а є R назив. Граничною точкою множини ХєR, якщо будь який окіл точки а містить нескінченну множину точок Х. |
|
Принцип: Всяка нескінченна обмежена множина має хоча б одну граничну точку. Нехай ХєR – нескінченна і обмежена. Існує
відрізок І=[a;b] Припустимо що Х не має граничних точок. Це значить що для будь якої точки х з відрізка І існує окіл що містить скінчене число точок множини Х. Обєднання всіх околів кожної точки Х містить в собі відрізок І(покриває). Цей відрізок є підмножиною обєднання околів. З
покриття U(x) можна виділити скінчене
під покриття тобто,
|
|
11.Границя числової послідовності. Обмеженість збіжної послідовності, єдиність границі. |
|
Озн:Число
а назив. границею числової послідовності
Хn (познач a=limXn) якщо для будь якого
околу точки а існує номер
|
|
Озн:Або для будь якого Е>0 знайдеться номер… такий що для всіх номерів більших виконується: |Xn-a|<E. |
|
Озн: Якщо існує границя то кажуть, що послідовність збіжна. |
|
Т: Збіжна послідовність обмежена
Тоді
| Т: збіжна послідовність не може мати дві різні границі. ->Від супротивного Припустимо
Тоді для E=|a1-a2|/3 Окіли цих точок не перетинаються Але за означенням для а1 існує номер Н1, що для всіх номерів більших за цей Хn лежить в околі точки а1. Аналогічно для а2. Виходить що Хn лежить в перетині околів цих точок… Але він пустий, маємо протиріччя
|
|
12.Нескінченно малі послідовності. Арифметичні властивості нескінченно малих. |
|
Озн: послідовність назив. Нескінчено малою якщо існує границя і вона рівна 0. |
|
Властивості: 1)Сума нескінчено малих є нескінчено мала Дано: limAn=limBn=0 Тоді за означ. Для будь якого Е>0 існує номер Н1, що для всіх номерів більших за Н1 |An-0|<E/2 Тоді за означ. Для будь якого Е>0 існує номер Н2, що для всіх номерів більших за Н2 |Bn-0|<E/2 Тоді для всіх номерів більших за максимальний з Н1 та Н2: |An+Bn|<=|An|+|Bn|<E/2+E/2=E Lim(An+Bn)=0 |
|
2)Добуток нескінч. Малої на обмежену – неск. Мала Нехай An-неск. Мала, Bn- обмежена
За озн. – Для Е>0 існує номер Н1,що для всіх номерів більших за Н1 |An-0|<E/M Тоді добуток для всіх номерів більших за Н1 |An*Bn-0|<E/M*M=E; |
|
Наслідки: 1)сума скінченого числа нескінчено малих – нескінченно мала. 2)добуток неск. Малої на число – неск. Мала. 3)якщо
|
|
13.Границя числової послідовності. Арифметичні властивості границі. |
|
1)Якщо
Записати означення для а без модуля, та з модулем |An|=An |a|=a, ||An|-|a||=|An-a| |
|
2)якщо існує limAn=a,limBn=b, то існує lim(An+Bn)=a+b За лемою кожну послідовність можна представити у вигляді сумми з неск. Малою: Існуть
такі
Тоді
An+Bn= |
|
3)lim(An*Bn)=limAn*limBn=a*b; |
|
4)lim(An/Bn)=limAn/limBn=a/b, b!=0 |
|
14.Границя числової послідовності. Граничний перехід в нерівністях. |
|
Т:Нехай
послідовності {Xn},{Yn},{Zn}
такі що Xn<Yn<Zn
для будь яких номерів, або для будь
яких номерів більших за деякий номер
n1,
і
За
означ. Для будь якого E>0
За
означ. Для будь якого E>0
Тоді для всіх номерів більших за max(N1,N2): a-E<Xn<Yn<Zn<a+E a-E<Yn<a+E |Yn-a|<E |
|
Т2:
нехай
a<b => E=b-a/3>0 За
означ. Для Хn:
=>Xn<a+b-a/3=2a-b/3 За
означ.
Для
Yn:
=>Yn<b-b-a/3=a+2b/3 Для всіх номерів більших за max(N1,N2): Xn<2a-b/3<Yn<a+2b/3=>Xn<Yn |
|
15.Перехід до границі у нерівностях, монотонні послідовності та їхні границі. |
|
Т:Нехай
послідовності {Xn},{Yn},{Zn}
такі що Xn<Yn<Zn
для будь яких номерів, або для будь
яких номерів більших за деякий номер
n1,
і
За
означ. Для будь якого E>0
За
означ. Для будь якого E>0
Тоді для всіх номерів більших за max(N1,N2): a-E<Xn<Yn<Zn<a+E a-E<Yn<a+E |Yn-a|<E |
|
Т2:
нехай
a<b => E=b-a/3>0 За
означ. Для Хn:
=>Xn<a+b-a/3=2a-b/3 За
означ.
Для
Yn:
=>Yn<b-b-a/3=a+2b/3 Для всіх номерів більших за max(N1,N2): Xn<2a-b/3<Yn<a+2b/3=>Xn<Yn |
|
Визнач. Послідовність an називають: Зростаючою, якщо хп<хп+1, для будь-якого n. Неспадною, якщо хп<=хп, для будь-якого n. Незростаючою, якщо хп>=хп, для будь-якого n. Спадною, хп>хп, для будь-якого n. В будь-якому з цих чотирьох випадків пслідовнісь називається монотонною. |
|
Т: Вейерштраса: Для того щоб неспадна(зростаюча) послідовність мала границю необх. Й достатньо щоб вона була обмежена зверху. (=>)Якщо існує границя то обмежена. (<=)An<An+1 для всіх n.
Тоді
для
An0<An<S |S-An|<|S-(S-E)|=E => S=limAn |
|
16. Монотонні послідовності |
|
Послідовність an називають: Зростаючою, якщо хп<хп+1, для будь-якого n. Неспадною, якщо хп<=хп, для будь-якого n. Незростаючою, якщо хп>=хп, для будь-якого n. Спадною, хп>хп, для будь-якого n. В будь-якому з цих чотирьох випадків пслідовнісь називається монотонною. |
|
Число е Розглянемо послідовність an = (1+1/n)^n і покажемо, що існує її границя. Скористаємося нерівісю бернулі (1+α)^n>=1+n*α. Метод М.І.: n = 1: 1+ α >= 1+ α n = k виконуэться krok: n = k+1 (1+ α)^(k+1) = (1+ α)^k*(1+ α)>=(1+k*α)(1+α) = 1+ k*α+α+k*α^2 = 1+(k+1)* α+k*α^2>=1+(k+1)*α –тобто нерівність виконується
В свою чергу:
|
|
17. Границя послідовності |
|
Послідовність
{xn}
називають фундаментальною, якшо
|
|
Критерий Коши Послідовність {xn} збігаєься тоді і тільки тоді, коли вона фундаментальна /доведення: 1)
(=>)дано: {xn}-збігається
=> тоді 2,)
(<=){xn}-фундаментальна
а)-покажемо, що вона обмежена
б)
будь-яка обмежена
послідовність має збіжну підпослідовність:
{xn}:=> Покажемо, що а єграницею для {xn}. {xn}-фундамент. => З
іншого боку:
(з
** випливає)=>
|
|
18. Часткові границі послідовності, верхня та нижня границі. |
|
Число
а або +-∞ називається частковою
границею послідовності {an},
якщо існує підпослідовність {ank}:
|
|
Визн . найбільша часткова границя {an} називається верхньою границею{an}, а найменша част. границя називається нижньою границею. |
|
Теорема Будь-яка послідовність має верхню та нижню границі. |
|
доведення Якщо
{an
}
небом. зверху, то існує піпослідовність
{ank}:
Якщо
послідовність {an
}
обмежена зверх, то можливі 2 випадки:
множина її часткових границь пуста,
або не пуста. Якщо скінченних граничних
точок немає, то існує тільки одна
часткова границя: -∞ =>
Якщо
існують скінченні граничні точки, то
множина граничних точок обмежена
зверху =>існує
supA=S.
Покажемо,
що S
–
часткова границя. Від супротивного.
Нехай S
не є граничною точкою {an
}
– це означає, що
|
|
Лема Якщо
За
умовою існує лім
Тоді
для
|
|
Теорема Послідовність {an} має границю коли її верхня границя співпадає з нижньою гран-ю. 1)(=>) лема 2)(<=)
Якщо
|

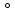 f:Х—Z,
що будується за правилом і для кожного
елемента х з множини Х - (g
f:Х—Z,
що будується за правилом і для кожного
елемента х з множини Х - (g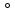 f)(х)=g(f(х))
f)(х)=g(f(х)) g
і g
g
і g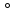 f,
то не значить, що f
f,
то не значить, що f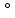 g=g
g=g f
f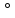 (g
(g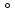 f)=(х
f)=(х g)
g)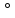 f,оскільки
для будь якого х з Х (х
f,оскільки
для будь якого х з Х (х (g
(g f)(х)=х((g
f)(х)=х((g f)(х))=х(g(f(х)))
f)(х))=х(g(f(х)))
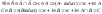
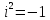 .
Нехай
Z1=a+bi, Z2=c+di
.
Нехай
Z1=a+bi, Z2=c+di
 =
= =>
Z=r
=>
Z=r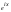

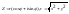
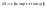

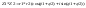


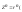
 )=
)=
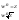 Нехай
W=|w|(
Нехай
W=|w|(
 )
)
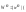
 )=Z=r(
)=Z=r( )
)
 =>
=>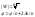 k=0,1,2…n-1;
k=0,1,2…n-1;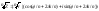
 b
b R,
що а<=b
для
R,
що а<=b
для
 A.
b
– верхня межа.
І обмеженою знизу якщо
A.
b
– верхня межа.
І обмеженою знизу якщо
 с
с
 R,
таке що а>=с для
R,
таке що а>=с для

 A.
Озн:
Якщо
множина обмежена зверху і знизу, вона
назив. Обмеженою
A.
Озн:
Якщо
множина обмежена зверху і знизу, вона
назив. Обмеженою
 (не пуста) обмежена зверху, тоді найменша
з її верхніх меж назив. точною верхньою
межею і позначається supA.
(не пуста) обмежена зверху, тоді найменша
з її верхніх меж назив. точною верхньою
межею і позначається supA.
 R
і
R
і

 А
а<=b,
тоді за аксіомою №5
існує число с
А
а<=b,
тоді за аксіомою №5
існує число с R
a<=c<=b.
R
a<=c<=b.
 A
<S
A
<S a*>S1
a*>S1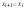 , тоді
це вкладена множина.
, тоді
це вкладена множина.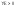
 і
і
 ,
то така точка єдина.
,
то така точка єдина. =[
=[ ]
] <=
<=

 N
N <=
<=
 >=
>= Тоді:
Тоді: <=
<= <=
<= <=
<=

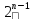 – нескінченно мала.
Тоді за принципом Коші кантора існує
точка с спільна с є
– нескінченно мала.
Тоді за принципом Коші кантора існує
точка с спільна с є
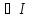 .
Значить
.
Значить

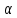 ;b
;b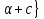 >0;
>0;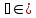 *:|In|<E
*:|In|<E
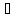 Х
Х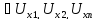 і обєднання цих околів теж покривають
відрізок І. Але кожний окіл містить
тільки скінчену кілкість точок Х.
Виходить шо Х має скінчене число точок,
що суперечить умові.
і обєднання цих околів теж покривають
відрізок І. Але кожний окіл містить
тільки скінчену кілкість точок Х.
Виходить шо Х має скінчене число точок,
що суперечить умові.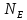 такий що для всіх n>
такий що для всіх n>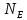 =>Xn
є U(a)
=>Xn
є U(a)
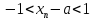
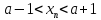
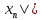 <max{|a-1|;|a+1|};
<max{|a-1|;|a+1|};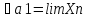
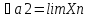
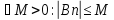
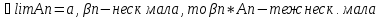
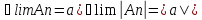
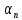 і
і
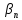 ,
що An=a+
,
що An=a+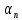 ,
Bn=b+
,
Bn=b+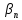
 +a+b
Тоді існує границя limAn+Bn=limAn+limBn;
+a+b
Тоді існує границя limAn+Bn=limAn+limBn; ,
то
,
то
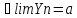 .
.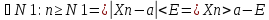
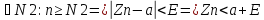
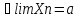 ,
,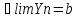 якщо a<b,
то
якщо a<b,
то


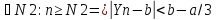
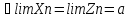 ,
то
,
то
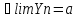 .
.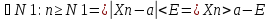

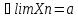 ,
,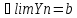 якщо a<b,
то
якщо a<b,
то
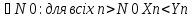
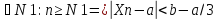
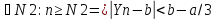

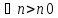
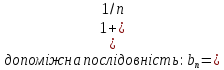
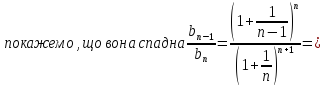
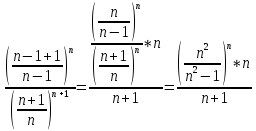
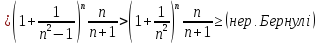
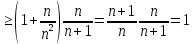
 обмежена
знизу послідовність. Тоді за наслідком
обмежена
знизу послідовність. Тоді за наслідком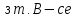
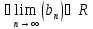
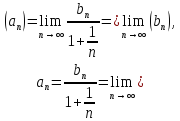
 тобто
ця границя існує,що і і треба було
довести.
е≈2,72
тобто
ця границя існує,що і і треба було
довести.
е≈2,72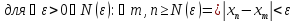
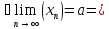
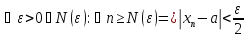
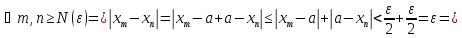 {xn}-фундаментальна
{xn}-фундаментальна Позначимо
через
М=max{|x1|,
|x2|,
…|xN1|,
|xN1|+1}
для будь-якого m
є N:
|xm|<=M.
Значить, {xn}-обмежена.
Позначимо
через
М=max{|x1|,
|x2|,
…|xN1|,
|xN1|+1}
для будь-якого m
є N:
|xm|<=M.
Значить, {xn}-обмежена.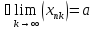


 =>
=>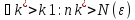
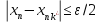 =>
=>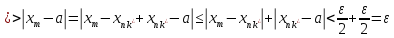 =>
=>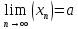 що
і треба було довести.
що
і треба було довести.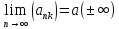 .
.
 =>
=>
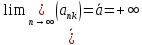
 .
.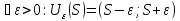 має
скінченне число точокз нашої
послідовності. Значить, в цьому околі
немає граничних точок {an
}
=>
S
не є supA,
що суперечить умові. Тобто, S
= maxA
=> S=
має
скінченне число точокз нашої
послідовності. Значить, в цьому околі
немає граничних точок {an
}
=>
S
не є supA,
що суперечить умові. Тобто, S
= maxA
=> S=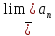 .
Аналогічно показуємо існування
нижньої границі.
.
Аналогічно показуємо існування
нижньої границі.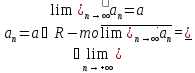


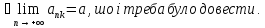
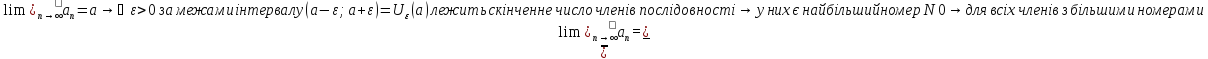 an
є
an
є