
ekzamen_шпора
.docx
|
19. Важливі границі |
|
1)
Наслідок
|
|
2)
з
попереднього приклада:
Наслідок
а) a>1
б) 0<a<1 --> 1/a > 1
|
|
3)
Оскільки
|
|
20. Границя функції. Означення за Коші та Гейне. Їх еквівалентність |
|
За Коші (І) Число
А наз. Границею функції f:
DR,
при хдо
a-гранична
для D,
якщо
|
|
(ІІ) А
називається границею функції f(x)
за
умови xa,
якщо для
|
|
За Гейне (ІІІ) Число
А назив. Границею функції
f:
DR,
при хдо
a-гранична
для D,
якщо для
|
|
Теорема Визначення І, ІІ, ІІІ – еквівалентні |
|
Доведення Схема: ІІІІІІІ 1.)ІІІІ Дано: Нехай
ІІІІІ Дано:
для
Припустимо,
що умова визначення ІІ не виконується,
тобто
Таким
чином, маємо послідовність Випливає одразу з визначення околів. |
|
21. Границя функції. Локальні властивості ф-ції, що має границю. |
|
Оскльки визначення за Гейне пов'язує границю ф-ції з границею послідовності => всі власт. границь послідовності переносяться на власт. границь ф-ції. А саме : 1)
Якщо
2)Якщо
|
|
Доведення.(від супротивного) Припустимо,
що
Тоді
для u10(a)
f(x)
Як і для послідовностей має місце : Якщо
1)
|
|
Наслідок 1 1)
Сума n нескінченно малих при х ->а
2) c 1)f(x),
g(x)
-- неск.
великі
при х
->а
2)Якщо
f(x)
- н.в. при х
->а
3)
f(x),
g(x)
-- неск.
великі
при х
->а
4)якщо
f(x)
- н.в., а g(x)
така що
f(x)*g(x)
- н.в. при х
->а
|
|
22.Границя складної (композиції) ф-цій |
|
нехай
x0,y0
-- граничні
точки, для множин Х,Y
відповідно
f:
X->Y
така,
що
|
|
Доведення
За
умовою
g(f(x))
= g(y) |
|
23. Власт. н.м. ф-цій Арифметичні власт. границі ф-ції |
|
Якщо
1)
|
|
Наслідок1 1)
Сума n нескінченно малих при х ->а
2) c |
|
Лема
|
|
Доведення
|
|
Використовуючи лему отримуємо: арифметичні власт. ф-цій, які мають границі: Якщо
1) 2) 3)Якщо
g(x) |
|
Наслідок Якщо
1) 2) 3) 4)
|
|
24. Перша чудова границя |
|
|
|
Доведення Область
визначення
f(-x)
=
|AD|= sin x, |OD| = cos x SOCD<S Ділимо
на
cos2
x
< |
|
25. Друга чудова границя |
|
|
|
Доведення Розглянемо 1-й випадок 1)
х -> при
х ->
Умови
теореми про границю композицій при
х0= В якості ф-ції g(y) візьмемо g0,g1.g2 : Z->R g0(n)=
(1+
тоді :
Але
(1+ |
|
26.Відношення О-велике, о-мале. Еквівалентні нескінченно малі, теорема про заміну в границях. |
|
Визначення1 Кажуть,
що ф-ція f(x)
є н.м. відносно ф-ції g(x)
при
x->a,
якщо
f(x)= |
|
Визначення2 Якщо,
|
|
Властивості : |
|
1)
Якщо
то при x->a ; f(x)= O(g(x)) g(x)= O(f(x)) Доведення
f(x)=
A g(x)= |
|
2) Якщо при х->а ; f(x)=O(g( (x))); g(x)=O(h(x))=> f(x)= O(h(x)) Доведення
f(x)
= f(x)= f(x)=O(h(x)) |
|
3) При х->a O(o(f(x)))=o(O(f(x)))=o(f(x)) Доведення
О(о(f(x)))
= O( Аналогічно: o(O(f(x))) = o(f(x)) |
|
Еквівалентні малі(визначення) Якщо
f(x)= |
|
Теорема Якщо
f1(x) 1) 2) коли хоча б ліва або права границя існують |
|
Доведення За
умовою f1(x) f2(x)=
Припустимо,
що
Аналогічно інші випадки. |
|
27.Таблиця еквівалентних нескінченно малих. |
|
1)
sin
x
2)
tg x
3)arcsin
x 4)
arctg
x
5)
ln(x+1) 6)ex-1 7)(1+x)a-1 8)1-cos
x |
|
28.Неперервні функції. Різні означення. Локальні властивості неперервних функцій. |
|
Нехай
х0 З власт. границь ф-цій => Якщо, f(x), g(x) - неперервні в т. x0 то: 1) f(x)+ g(x)- неперервна в т. x0 2) f(x)* g(x)- неперервна в т. x0 3)Якщо
g(x) 4) Неперервність композиції ф-цій Якщо
f(x)-
неперервна в т. x0,
g(y)-
неперервна
в т. у0
=f(x0),
то
композиція (g |
|
Локальні власт. неперервних ф-цій. Теорема Якщо f: D->R - неперервна в т. х0, то 1)Вона обмежена в деякому окілі uD(x0) 2)
Якщо
f(x0)
Доведення 1) властивість ф-ції , що має скінченну границю 2)Нехай
f(x0)>0
|
|
Теорема Якщо
g:
X->Y
- неперервна
в т. х0 |
|
29.Неперервність складної функції. Точки розриву. |
|
Теорема Якщо
g:
X->R
- неперервна
в т. х0 |
|
Точки розриву ф-ції Нехай f(x) - визначена в деякому u0(x0) , точка x0 назив. т. розрива ф-ції f(x) якщо: 1) f(x) - невизначена в т. х0 2) |
|
Точки розриву поділяються на 2 роди: Точки
розрива х0
ф-ції f(x)
назив. точкою розрива 1-го рода, якщо
1) 2) Якщо
хоча б одна з
При
чому, якщо існують обидві границі, але
хоча б одна з них
|



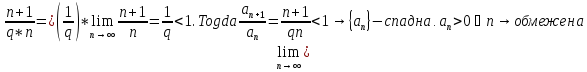

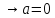










 .
.

 .
.

 – довільна послідовність така, що
– довільна послідовність така, що .Тоді
за визначенням границі
.Тоді
за визначенням границі


 ,
Що
суперечить умові, тобто припущення
хибне.
ІІІ
,
Що
суперечить умові, тобто припущення
хибне.
ІІІ =
A
=
A R,
то
R,
то
 u0
в якому f(x)
обмежена.
u0
в якому f(x)
обмежена. =
A
=
A R,
то
вона єдина
R,
то
вона єдина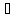 2 границі
2 границі
 =А,
=А,
 = В, А
= В, А =>
=>
 u(A)
i
u(A)
u(A)
i
u(A) u(B)
=
u(B)
=
 }
} =A
=>
=A
=> u10
(a)
:
u10
(a)
:
 x
x
 u10
(a)
=>
f(x)
u10
(a)
=>
f(x)
 u(A)
u(A) В
=>
В
=>
 u20(a)
:
u20(a)
:
 x
x
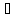 u20(a)
=>
f(x)
u20(a)
=>
f(x)
 u(В)
u(В) u20(a)
=>
u20(a)
=>
 x
x u0(a)
=>
f(x)
u0(a)
=>
f(x)
 ,
, =>
u(A)
=>
u(A) u(B)
u(B)
 }
-- суперечить умові
}
-- суперечить умові
 (х)
- н.м. при х ->а,
то
(х)
- н.м. при х ->а,
то (х)
= н.м. при х ->а
; 2)
(х)
= н.м. при х ->а
; 2) -- локально обмеженої
при х ->а
-- локально обмеженої
при х ->а
 *
* = н.м.
= н.м. є
н.м.
є
н.м.
 = н.м.
при х ->а
= н.м.
при х ->а

 одного
знаку, то f(x)+
g(x)
- н.в. при х
->а
одного
знаку, то f(x)+
g(x)
- н.в. при х
->а

 ,
а g(x)--
локально обмежена при х
->а
,
а g(x)--
локально обмежена при х
->а
 ,
то f(x)+
g(x)
= н.в.
,
то f(x)+
g(x)
= н.в. f(x)*g(x)=
н.в. при х
->а
f(x)*g(x)=
н.в. при х
->а

 М>0
і
М>0
і
 u0(a):
g(x)
u0(a):
g(x) М,
М,
 x
x u0(a),
то
u0(a),
то
 =y0
=y0 =A
Тоді ,якщо
=A
Тоді ,якщо
 uY0(y0)
uY0(y0)
 uX0(x0)
такий, що f(uX0(x0)
uX0(x0)
такий, що f(uX0(x0)
 uY0
(y0)
, то
uY0
(y0)
, то
 =
= =
=
 =
A
=
A =A
=>
=A
=> :
:
 u0у(y0):
g(uy(y)
u0у(y0):
g(uy(y) u(A)
u(A) uX0(x0):
f(uX0
(x0)
uX0(x0):
f(uX0
(x0) (uY0
(y0)=>
∀x∈u0(x0)
маємо f(x)=y∈
u0(y0)=>
(uY0
(y0)=>
∀x∈u0(x0)
маємо f(x)=y∈
u0(y0)=> u(A) =>
u(A) => (x)
= g(f(x))
(x)
= g(f(x)) u(A)
=>
u(A)
=>
 =
А =
=
А =
 (х)
- н.м. при х ->а,
то
(х)
- н.м. при х ->а,
то (х)
= н.м. при х ->а
; 2)
(х)
= н.м. при х ->а
; 2) -- локально обмеженої
при х ->а
-- локально обмеженої
при х ->а
 *
* = н.м.
= н.м. є
н.м.
є
н.м.
 = н.м.
при х ->а
= н.м.
при х ->а

 =
A
=
A R
R
 f(x)
= A +
f(x)
= A +
 ,
де
,
де
 --
н.м.(x-->a)
--
н.м.(x-->a) =
A
=
A R
R >
>
 :
:
 0
:
0
0
:
0 => |f(x)-A|<
=> |f(x)-A|< ,
або
позначивши
,
або
позначивши f(x)
- A;
|
f(x)
- A;
| |
<
|
<

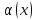 -- н.м.
при х-
-- н.м.
при х-
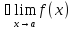 =А;
=А;
 В,
то:
В,
то: g(x))= A+B =
g(x))= A+B =
 +
+

 g(x))= AB =
g(x))= AB =
 *
*

 0,
B
0,
B ,
то
,
то
 g(x))=
А/В =
g(x))=
А/В =
 /
/

 =Аi
, i=(0...n),
то:
=Аi
, i=(0...n),
то: =
A1
+ A2
+...+An
=
A1
+ A2
+...+An =
A1
* A2
*...*An
=
A1
* A2
*...*An N
,
N
,
 =(
=( )^k
)^k ,
,
 =c*
=c*
 )
= 1
)
= 1 - D:R/{0}
- D:R/{0} -
ф-ція парна ;
-
ф-ція парна ; =
=
 =
=

 можна
розглядати тільки х
можна
розглядати тільки х 0
0 OAB<Sдуги
OAB
,
Sсек
<
OAB<Sдуги
OAB
,
Sсек
< R2*
R2*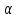 ,
,
 *х*cos2x<
*х*cos2x<
 <
< x
x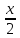 >0
>0
 <1
,
1-sin2x<
<1
,
1-sin2x< <1
=>
<1
=>
 --> 1
--> 1 x
=
e
x
=
e , нехай
Х = (0;
, нехай
Х = (0; )
, Y=Z,
f:
X->Y
за правилом f(x)=[x]=
sup(y
)
, Y=Z,
f:
X->Y
за правилом f(x)=[x]=
sup(y Z(y
Z(y )
) => f(x)->
=> f(x)-> , x-1
, x-1 [x]
[x]

 uY(
uY( = (n;
= (n; ,
,
 >
n ; f(u(B;
>
n ; f(u(B; ))
)) uY(
uY( )
) у0=
у0= виконані
виконані )n
, g1(n)=
(1+
)n
, g1(n)=
(1+ )n
, g2(n)=
(1+
)n
, g2(n)=
(1+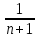 )n+1
)n+1 n
=
e
n
=
e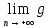 1(n)=
1(n)= n=
n=
 n*
n* *(n+1)
=
*(n+1)
=
 =e
=e 2(n)
=
2(n)
= n+1
= )=
n+1
= )= n
*)=
n
*)= =
e*1=e
=
e*1=e (x))=
(x))=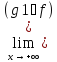 (x))=
(x))= (x))=e
(x))=e маємо:
маємо: )[x]
)[x]
 (1+
(1+ )x
)x (1+
(1+ )[x]+1
=>(1+
)[x]+1
=>(1+ )x
-->
e
)x
-->
e (x)*g(x),
де
(x)*g(x),
де
 (x)-
н.м. при x->a
, позначення
f(x)
= o(g(x))
при
x->a
(x)-
н.м. при x->a
, позначення
f(x)
= o(g(x))
при
x->a u0(a)
і обмежена в цьому окілі ф-ція
u0(a)
і обмежена в цьому окілі ф-ція
 (х)
така, що f(x)=
(х)
така, що f(x)= (х)*g(x),
то
кажуть , що f(x)=O(g(x))
при
x->a
(х)*g(x),
то
кажуть , що f(x)=O(g(x))
при
x->a = A ; A
= A ; A 0;
A
0;
A
 =
А
=>
=
А
=>
 -- обмежена
в u0(A)
-- обмежена
в u0(A) *g(x)
= O(g(x))
*g(x)
= O(g(x)) 0
=>
0
=>
 =
=
 ;
;
 0;
0;
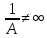
 *f(x) = O(f(x))
*f(x) = O(f(x)) 1(х),
1(х),
 2(х)
-- обмежені в u0(a):
f(x)
=
2(х)
-- обмежені в u0(a):
f(x)
= 1(х)*
g(x)
i
g(x)=
1(х)*
g(x)
i
g(x)= 2(х)*h(x)=>
2(х)*h(x)=> 1(х)*
1(х)* 2(х)*h(x)
2(х)*h(x) 1(х)(
1(х)( 2(x))*h(x)=
2(x))*h(x)= h(x)=>
h(x)=> (х)
- н.м. і
(х)
- н.м. і
 (х)
- обмежена при х->a
такі
, що :
(х)
- обмежена при х->a
такі
, що : (x)*f(x))=
(x)*f(x))= (x)(
(x)( (x)*f(x))=
(x)*f(x))=
 (x)*f(x)=
O(o(f(x)))=o(f(x))
(x)*f(x)=
O(o(f(x)))=o(f(x)) g(x)
i
g(x)
i
 =1,
то кажуть, що при х->a
f(x)
еквівалентна g(x)
і позначають :
f(x
=1,
то кажуть, що при х->a
f(x)
еквівалентна g(x)
і позначають :
f(x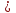 g(x)
при
х->a
g(x)
при
х->a
 g1(x),
f2(x)
g1(x),
f2(x) g2(x)
при
x->a,
то
g2(x)
при
x->a,
то (f1(x)*
f2(x))=
(f1(x)*
f2(x))= (g1(x)*
g2(x))
(g1(x)*
g2(x)) (
( )=
)= (
(
 g1(x),
f2(x)
g1(x),
f2(x) g2(x)
при
x->a
=>
g2(x)
при
x->a
=>
 1(x)
1(x) 2(x)=>
f1(x)=
2(x)=>
f1(x)= 1(x)g1(x);
1(x)g1(x); 2(x)*g2(x)
при
чому
2(x)*g2(x)
при
чому
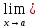 (
( 1(x))=
1(x))= (
( 2(x))=1
2(x))=1 (
( )
= A.
Тоді
)
= A.
Тоді
 (
( =
= (
( =
= A=A
A=A x (
x ( = 1)
= 1) x (
x ( )=1)
)=1) (
( =
=
 =
= (
( )=1)
)=1) --
доведення
аналогічне
--
доведення
аналогічне
 x
(
x
( =
= =
= =ln
e=1)
=ln
e=1) (
( (
( )={ex-1
=t; ex=1+t->xln(1+t)}=
)={ex-1
=t; ex=1+t->xln(1+t)}= (
( )=1)
)=1) (
( )=
)= =
= =1)
=1) (1-cos x=2sin2
(
(1-cos x=2sin2
( )
) 2(
2( )2
=
)2
=
 D
-- гранична
для D
f:D->R
назив.
неперервною
в т. х0
,
якщо
D
-- гранична
для D
f:D->R
назив.
неперервною
в т. х0
,
якщо
 (f(x))=f(x0)
(f(x))=f(x0) 0,
то
0,
то
 -- неперервна
в т. x0
-- неперервна
в т. x0 f)(x)
- теж
неперервна в т.х0
f)(x)
- теж
неперервна в т.х0 0,
то
в деякому окілі
0,
то
в деякому окілі
 х
х u
u u(x0):
sign(f(x))=sign(f(x0));
u(x0):
sign(f(x))=sign(f(x0));
 u(а)
u(а)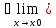 (f(x))=f(x0)
=> для
(f(x))=f(x0)
=> для
 =
=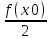 >0
>0
 u(x0):
x
u(x0):
x u(x0)
=> |f(x)-f(x0)|<
u(x0)
=> |f(x)-f(x0)|< =>
=> <
f(x)-f(x0)
=> f(x)>f(x0)-
<
f(x)-f(x0)
=> f(x)>f(x0)- =
= >0
>0 - граничній для Х і f(x0)
= y0,
то
g
- граничній для Х і f(x0)
= y0,
то
g f:
X->R
теж
неперервна в т.х0
f:
X->R
теж
неперервна в т.х0 - граничній для Х і f(x0)
= y0,
то
g
- граничній для Х і f(x0)
= y0,
то
g f:
X->R
теж
неперервна в т.х0
f:
X->R
теж
неперервна в т.х0 f(x0),
але
ф-ція f(x)
не є неперервною в т. х0
f(x0),
але
ф-ція f(x)
не є неперервною в т. х0 (f(x))єR
і
(f(x))єR
і (f(x))
єR
,
при
чому :
(f(x))
єR
,
при
чому : (f(x))=
(f(x))= (f(x))--
усувний
розрив
(f(x))--
усувний
розрив (f(x))
(f(x)) (f(x))--скінченний
стрибок
(f(x))--скінченний
стрибок (f(x)),
(f(x)), (f(x))
дорівнює
(f(x))
дорівнює
 ,
або не існує => т.х0
- точка
розриву 2го роду
,
або не існує => т.х0
- точка
розриву 2го роду
 => розрив 2го роду, нескінченний
стрибок,
а якщо хоча б одна з них не існує =>
т.х0
- точка
розриву 2го роду, суттєвий
розрив
=> розрив 2го роду, нескінченний
стрибок,
а якщо хоча б одна з них не існує =>
т.х0
- точка
розриву 2го роду, суттєвий
розрив