
ekzamen_шпора
.docx
|
30.Властивості неперервних функцій на відрізку: теорема Больцано-Коші. |
|
Теорема Больцано- Коші Якщо
f:[a;b]
-->R
- неперервна на [a;b]
і приймає на його кінцях знач. різних
знаків, то
|
|
Визначення Ф-ція
f:D->R
назив. неперервною на D,
якщо вона неперервна в
|
|
Доведення f(a)-f(b)<0 Поділимо
відрізок ( Якщо f(с)=0 => теорема доведена Якщо
f(с) З відрізка [a1;b1] поступаємо таким же чином: ділимо навпіл і тд Якщо
ні в одній з середин f(с) [a;b]=[a0;b0] З
леми про вкладені відрізки існує єдина
спільна точка с є [an;bn]
Позначимо через х'n -- ті кінці відрізків, в яких f(х'n)<0 і x''n --||-- f(x''n)>0 => х'n
-->
c
(n
-->+ З неперервності f(x) в т. с
|
|
Наслідок Якщо f(x) -- неперервна на [a;b] , f(a)=A, f(b)=B, ∃q∈(a;b) така, що f(q)=Q |
|
Доведення Розглянемо g(x) = f(x) - Q -- неперервна на [a;b] g(a)=f(a)-Q= A-Q g(b)=f(b)-Q = B-Q i g(a) - g(b)=(A-Q)(B-Q)<0 => ∃q∈(a;b): g(q)=0 => f(q)-Q => f(q)=Q |
|
31.Властивості неперервних функцій на відрізку: теорема Вейєрштрасса. |
|
Tеорема Вейєрштрасса Ф-ція неперервна на відрізку [a;b], обмежена цьому відрізку. При цьому на [a;b] є точки хm , xM в яких f(x) приймає своє найменше і найбільше знач. |
|
Доведення 1.Обмеженість ∀х∈[a;b]
∃ mx≤f(t)≤Mx ∀t∈ u(x) => Uxє[a;b]u(x)⊃[a;b] => за лемою про скінченне підпокриття => можна виділити скінченне підпокриття тобто, існують u (xі), і = 1,2,..,n, що U^n(i=1)u(xi) ⊃ [a;b], за побудовою ∀i=1...m ; mi≤f(t) ≤Mi ∀t∈ u(xi), позначимо через m=min(m1,m2,...,mn); M=max(M1,M2,..,Mn). Тоді ∀х∈[a;b] ∃і=1... n, що х∈u(xi) =>m≤mi≤f(x) ≤Mi≤M => m≤f(x) ≤M ∀х f(x) -- обмежена на [a;b] 2. f(x) -- обмежена на [a;b] => ∃S=sup[a;b]f(x)∈R; I=inf[a;b]f(x) ∈R Покажемо, що ∃xm:f(xm)=I; ∃xM:f(xM)=S; Від супротивного: Припустимо, що ∄хм∈[a;b] такий, що f(xm)=S => не існує на [a;b] т. хм в якій S-f(x)=0 Розглянемо
ф-цію g(x)=
Значить, вона обмежена на [a;b]. Але за визначенням для ∀ε>0 ∃x ε∈[a;b] : f(x ε)>S- ε; Тоді g(xε)- необмежена на [a;b] Це суперечить з 1 => припущення хибне Аналогічно показуємо, що ∃xm∈[a;b]; f(xm)= I |
|
32.Рівномірно-неперервні функції. Теорема Кантора. |
|
Рівномірна неперервність ф-ції -- це положення, яке теж відноситься не до точки, а до обл. визначення ф-ції, або деякої її підмножини. |
|
Визначення f(x) назив. рівномірно неперервною на D, якщо ∀ε>0 ∃δ>0 : |x1-x2|< δ ∀x1,x2∈D => |f(x1)-f(x2)|< ε Якщо, f(x) - рівномірно неперервна на D, то вона неперервна на D. |
|
Теорема Кантора Ф-ція неперервна на відрізку [a;b] буде рівномірно неперервною на ньому |
|
Доведення f(x) -- неперервна на цьому відрізку, зафіксуємо довільну ε>0 ∀х∈[a;b],
f--
неперервна в т. х => ∃δ(x)>0
=> ∀t
∈uδ(x)(x)
; |f(t)-f(x)|< Ux∈[a;b] uδ(x)/2(x) ⊃[a;b] => за лемою про скінченне підпокриття => ∃ скінченне підпокриття, тобто ∃х1,х2,...,хn Un(i=1) uδ(x)/2(xi) ⊃[a;b] Позначимо
δ = min{ Тоді ∀х1, х2 ∈ [a;b] таких, що |x1-x2|< δ ∃i : uδ(x)/2(xi) =>|x2 -xi|= |x2-x1+x1-xi|≤|x2-x1|+ +|x1-xi|< Тоді
|f(x2)-f(x1)|=
|f(x2)-f(xi)|+|f(xi)-f(x1)|≤
|f(x2)-f(xi)|+|f(x1)-f(xi)|< |
|
33. Диференціал та похідна. Неперервність диференційованої функції. |
|
Ф-ція f: D-->R назив. диференційованой в т. х0, якщо ∃А ∈ R таке, що в цій точці ∆у=А*∆х+ о(∆х) при ∆х -->0; (f(x)-f(x0))=A(x-x0)+ o(x-x0) при x-->x0 В цьому випадку вираз А*∆х назив. диференціалом ф-ції f(x) в т. х0 і позначається : dy=A *∆x Диференціалом незалежної змінної х назив. її приріст dx = ∆x=x-x0 |
|
Визначення Величина
|
|
Теорема Ф-ція
у= |
|
Доведення 1)(=>) Дано, f(x) -- диференц. в т. х0 => ∃А - const, що ∆у=А*∆х + о(∆х) при ∆х--> 0 Тоді
f'(x0)
=
2)(<=)
Дано, ∃ f'(x0)= A |
|
Зв'язок неперервності та диференц. ф-ції. Теорема Якщо y=f(x) диференц. в т. х0, то вона неперервна в т х0 |
|
Доведення f(x)-- диференц. в т. х0 => ∆f= f(x) -f(x0)= f'(x0)(x-x0) +o(x-x0) f(x)=
f(x0)+
f'(x0)(x-x0)+
o(x-x0)
=>
f(x0)+0+0= f(x0) => f(x) -- неперервна в т. х0 Навпаки неправильно. Неперервна в т.х0 ф-я може не мати похідної в цій точці. |
|
34.Арифметичні властивості похідної, диференціювання добутку та частки. Таблиця похідних. |
|
Нехай ф-ції y1 = f1(x); y2=f2(x) визначені в u(x0) i диференц. в т. х0 Тоді їх сума, добуток, а при f2(x0)≠0, і добуток в т. х0 при чому : 1)
(f1
+f2)'=
f'1
+f'2;
2)(f1*f2)'
=f'1*f2
+ f1*f'2
; 3)( |
|
Доведення 1) y= f1(x) +f2(x) => ∆y=y(x0+∆x)-y(x)= f(x0+∆x)+ f2(x+∆x)-f1(x)-f2(x)= ∆y1 + ∆y2
∃y'(x0)= y'1(x0)+ y'2(x0); 2)y= f1(x)f2(x) => ∆y = f1(x0 +∆x)f2(x0+∆x)-f(x0)f2(x0)= f1(x0 +∆х)(x0+∆х)-f1(x0)f2(x0+∆x)+f1(x0)f2(x0+∆x) -f1(x0)f2(x0)= ∆y1 *f2(x0+∆x)+ ∆y2f1(x0) =>
3)
y= ∆y
=
|
|
Табл. похідних 1)
f(x)=C
-const; => ∀x ∆y=C
-C=0 => y'= 2)f(x)=xn, n∈N -- за ф-лою бінома Ньютона маємо: ∆y=f(x+∆x)-f(x)= (x+∆x)n-xn =xn+C1nxn-1∆x +C2nxn-2∆x2+...+∆x2-xn = nxn-1∆x+(C2nxn-2∆x +...+∆xn-1) ∆x ∀x∈R
3)y=sin x ∀x∈R
4)Аналогічно (cos x)' = -sin x 5)f(x)=ax
=>
|
|
35. Диференціювання складних функцій та функцій, заданих параметрично. Таблиця похідних. |
|
Нехай ф-ція y=g(x) має похідну в т. х0, а ф-ція z=f(y) має похідну в т. х0 , y0=g(x0) Тоді складена ф-ція F(x)=f(g(x))=(f °g)(x) теж має похідну в т. х0 при чому F'x(x0)=fy(y0)gx(x0) |
|
Доведення z=f(y) - диференц. в т. у0
{y=g(x);
|
|
36.Похідна складеної функції. Інваріантність форми першого диференціалу |
|
Нехай
функція y=g(x) має похідну в т х0, а функція
z=f(y) має похідну в точці у0= g(x0). Тоді
складена функція F(x)=f(g(x))=(f○g)(x)
теж має похідну в т. х0, причому
|
|
доведення z=f(y)
– диференційована в т. у0 =>
|
|
Наслідок (Інваріантність форми першого диференціала)
|
|
доведення
|
|
37. Диференціювання неявної та оберненої функцій |
|
Похідна оберненої функції Нехай
функція у=у(х) – неперервна, строго
монотонна в околі точки х0 і диференційована
в т.х0, при чому y’(x0)!=0. Тоді обернена
функція х = х(у) має похідну в точці
у0=у(х0), причому
|
|
доведення у=у(х) – строго монотонна в околі т.х0 => існує обернена до неї х = х(у) тогож характеру монотон-і. у(х) – неперервна в т. х0 => x=x(y) – неперервна в т у0 і в цих точках ∆x0∆y0
|
|
Похідна неявно заданої функції Якщо
ф-я у=у(х) в околі точки (х0;у0) визнач
рівнянням F(x;y)=0,
то похідну
|
|
38. Похідні та диференціали вищих порядків . Формула Лейбніца |
|
Похідні вищих порядків Нехай f: DR Якщо
f
– диференційована в кожній точці D,
то на D
визначена функція
Загалом,
похідною н-ого порядку ф-ії f
називається похідна
|
|
Приклади: 1) 3) |
|
Формула Лейбніца Відомо:
Узагальнення: формула Лейбніца
|
|
Доведення
за
ММІ: 1) n=1
=> 2)
припустимо, що для n
формула має місце, тоді для n+1
маємо
|
|
Диференціали вищих порядків Якщо
Диференціалн-ого
порядку за індукцією:
|
|
Властивості
|
|
39.Теорема Ферма. Теорема Ролля. |
|
Якщо
функція
|
|
Доведення
f(x)
–
диференційована
в точці x0
⇒
Δf
= f(x)
– f(x0)
= f’(x0)*
Δx
+ o(Δx),
при Δx
→ 0. Тоді
f(x)
– f(x0)
= (f’(x0)
+ α(Δx))*Δx,
x
= x0
+ Δx.
Припустимо, що f’(x)
≠ 0.
lim
α(Δx)
= 0 ⇒ ε
=
|
|
Теорема Ролля Якщо f:[a;b] → R неперервна на [a;b] диференційована на (a;b) і f(a) = f(b) то існує c ∈ (a;b) Доведення Оскільки функція f(x) неперервна на проміжку [a;b] то, згідно з другою теоремою Вейєрштрасса, ця функція досягає на ньому свого максимального значення M та мінімального значення m. Отже, маємо два випадки: M = m або M > m .В першому випадку f(x) = M = m = const. Тому похідна f’(x) дорівнює нулю в будь-якій точці проміжка [a;b] У випадку, коли M > m, оскільки f(a) = f(b), можна стверджувати, що хоча б одне з двох значень M чи m досягається функцією в деякій внутрішній точці c проміжка [a;b]. Але тоді функція f(x) має у точці c локальний екстремум. Оскільки функція f(x) диференційовна в точці c, то за необхідною умовою локального екстремуму, f’(x) = 0. |
|
40. Теорема Ролля. Теорема Лагранжа |
|
Якщо f:[a;b] → R неперервна на [a;b] диференційована на (a;b) і f(a) = f(b) то існує c ∈ (a;b) Доведення Оскільки функція f(x) неперервна на проміжку [a;b] то, згідно з другою теоремою Вейєрштрасса, ця функція досягає на ньому свого максимального значення M та мінімального значення m. Отже, маємо два випадки: M = m або M > m .В першому випадку f(x) = M = m = const. Тому похідна f’(x) дорівнює нулю в будь-якій точці проміжка [a;b] У випадку, коли M > m, оскільки f(a) = f(b), можна стверджувати, що хоча б одне з двох значень M чи m досягається функцією в деякій внутрішній точці c проміжка [a;b]. Але тоді функція f(x) має у точці c локальний екстремум. Оскільки функція f(x) диференційовна в точці c, то за необхідною умовою локального екстремуму, f’(x) = 0. |
|
Теорема
Лагранжа
Якщо
f:[a;b]
→ R
неперервна на [a;b]
диференційована
на (a;b)
то існує
c
∈ (a;b):
f(b)
– f(a)
= f’(c)*(b-a)
Доведення
Розглянемо
на проміжку [a,b] наступну
допоміжну функцію:
Згідно
з теоремою Ролля на проміжку (a;b) знайдеться
точка c така,
що
З рівності (2) витікає формула Лагранжа.
|
|
41. Теорема Лагранжа. Наслідки з теореми Лагранжа Якщо f:[a;b] → R неперервна на [a;b] диференційована на (a;b) то існує c ∈ (a;b): f(b) – f(a) = f’(c)*(b-a) Доведення
Розглянемо
на проміжку [a,b] наступну
допоміжну функцію:
Згідно
з теоремою Ролля на проміжку (a;b) знайдеться
точка c така,
що
З рівності (2) витікає формула Лагранжа. |
|
Наслідки з теореми Лагранжа 1. Якщо в кожній точці інтервалу (a;b) виконується умова f’(x) = 0, то функція є сталою на цьому інтервалі. 2. Якщо в кожній точці інтервалу (a;b) виконується умова f’(x) = g’(x), то функція f(x) і g(x) на (a;b) відрізняються на сталу величину. |
|
42. Наслідки з теореми Лагранжа. Теорема Коші |
|
Наслідок
1(про монотонну функцію)
Якщо в усіх
точка (a;b)
похідна
f’(x)
функції
|
|
Доведення
|
|
Теорема
Коші
Нехай
f(x);
g(x)
є
С([a;b])
диференц. на (a;b)
при чому g’(x)
не дорівнює
0. Тоді
|
|
43 - 44. Правило Лапіталя |
|
Нехай
f(x)
і
g(x)
визначені
на [a;b]
і
такі що:
f(a)
= g(a)
= 0; ∃
f’(a);
g’(a).
Тоді
існує
|
|
Доведення
для
f(x) i g(x) – диференційовані в т. a ⇒
|
|
Доведення
для
|
|
45. Формула Тейлора |
|
|

 т.с
є (a;b):
f(с)=0
т.с
є (a;b):
f(с)=0 хєD
хєD )
навпіл точкою с=
)
навпіл точкою с=
 0
=> тоді f(a)*f(с)<0
або f(c)*f(b)<0
=> отримуємо відрізок [a;b]
такий, що f(a1),f(b1)<0
i
0
=> тоді f(a)*f(с)<0
або f(c)*f(b)<0
=> отримуємо відрізок [a;b]
такий, що f(a1),f(b1)<0
i

 0
=>
отримуємо
послідовність вкладених відрізків
0
=>
отримуємо
послідовність вкладених відрізків [a1;b1]
[a1;b1] ...
... [an;bn];
|[an;bn]|=
[an;bn];
|[an;bn]|= -->0(n -->+
-->0(n -->+ f(an)*f(bn)<0
f(an)*f(bn)<0 n
n , x''n
-->0 (n
-->+
, x''n
-->0 (n
-->+ , | x''n
-c|-->0
(n
-->+
, | x''n
-c|-->0
(n
-->+
 =>
f(c)=0
=>
f(c)=0 =f(x)
=> ∃u(x):f(t)
-- обмежена в u(x)
тобто, ∃ такі mx
i
Mx
:
=f(x)
=> ∃u(x):f(t)
-- обмежена в u(x)
тобто, ∃ такі mx
i
Mx
: -- неперервна
на [a;b]
і в 0 не обертається
-- неперервна
на [a;b]
і в 0 не обертається
 }>0
}>0 +
+ <
<
 i)
=> x1,x2
∈
uδ(xi)(xi)
i)
=> x1,x2
∈
uδ(xi)(xi) = ε;
= ε; =
= = f'(x0),
якщо існує назив. похідною
ф-ції в
т х0
= f'(x0),
якщо існує назив. похідною
ф-ції в
т х0 --
диференц. в т. х0
<=>
∃
f'(x0),
при
чому dy=
f'(x0)dx
--
диференц. в т. х0
<=>
∃
f'(x0),
при
чому dy=
f'(x0)dx =
= =
=
 =A
=A =>
=>
 = f'(x0)
+ α(
= f'(x0)
+ α( x)
при
x)
при
 -->0
=>
-->0
=>
 =
f'(x0)
=
f'(x0) +
α(
+
α( x)
x) =
= +
о(∆х),
де
А=
f'(x0)
=>
dy
= v)dx
+
о(∆х),
де
А=
f'(x0)
=>
dy
= v)dx (f(x0)
+ A(x-x0)
+ o(x-x0))
= f(x0)+A
(f(x0)
+ A(x-x0)
+ o(x-x0))
= f(x0)+A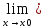 (x-x0)+
(x-x0)+ (o(x-x0))=
(o(x-x0))= )'=
)'= ;
; =
=
 =
=
 +
+ = f'1(x0)+
f'2(x0)
=>
= f'1(x0)+
f'2(x0)
=>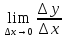 =
=
 =
= +
+ =
=
 *
* (f2(x0+∆x))+
(f2(x0+∆x))+ f1(x)
f1(x) (
( )=
f'1(x)*f2(x)
+ f1(x)*f'2(x)
)=
f'1(x)*f2(x)
+ f1(x)*f'2(x)
 -
-
 =
=
 =
=

 (
( =
=
 (
( )*
)* f1(x0)
f1(x0)
 = =
= = ;
; (
( =
= (
( =0
=0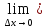 (
( =
= (nxn-1+
C2nxn-2∆x
+...+∆xn-1)=
nxn-1
(nxn-1+
C2nxn-2∆x
+...+∆xn-1)=
nxn-1 =sin(x+
=sin(x+ )-sin(x)=2sin(
)-sin(x)=2sin( )*cos(x+
)*cos(x+ )
)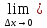 (
( =
= (
( )=
)= (
( *
cos(x+
*
cos(x+ )=cos
x
)=cos
x =a(x+∆x)-ax
= ax(a∆x
-1)
=a(x+∆x)-ax
= ax(a∆x
-1) (
( =
= (
( )=ax
)=ax (
( )=axln
a
)=axln
a z=fy(y0)
z=fy(y0) +o(
+o( z)=fy'(y0)
z)=fy'(y0) +α(
+α( y)
y) (при
(при
 0)
0) =gx'(x0)+o(
=gx'(x0)+o( )}
; fy'(y0)gx(x0)
)}
; fy'(y0)gx(x0) +fy'(y0)
+fy'(y0)




 -
диференціал фун-ії дорівнює добутку
пох. ф-ії по змінній на диференціал
цієй змінної, незалежно від того, яка
ця змінна: незал, чи ф-яякоїсь змінної
-
диференціал фун-ії дорівнює добутку
пох. ф-ії по змінній на диференціал
цієй змінної, незалежно від того, яка
ця змінна: незал, чи ф-яякоїсь змінної



 можна знайти використовуючи теорему
про похідну складеної функції без
розв’язку рівняння F(x;y)=0
продифференціював по х тотожність
F(x;y)=0
можна знайти використовуючи теорему
про похідну складеної функції без
розв’язку рівняння F(x;y)=0
продифференціював по х тотожність
F(x;y)=0
 :
DR.
Якщо ця ф-я диференційована в т х0 є D,
то її похідна по відношенню до функції
f
називається другою похідною і
позначається
:
DR.
Якщо ця ф-я диференційована в т х0 є D,
то її похідна по відношенню до функції
f
називається другою похідною і
позначається
 в т. х0. Позначення:
в т. х0. Позначення: .
Похідна нульового порядку – сама
функція f.
.
Похідна нульового порядку – сама
функція f. 2)
2)
 =>
=>
 ;
;
 ;
;
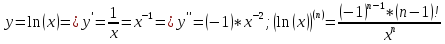




 (з
другої суми беремо перший доданок, а
з першої суми останній)=
(з
другої суми беремо перший доданок, а
з першої суми останній)=



 - диференційована ф-ія змінної х, то
диференціал цієй функції називається
другим диференціалом функції y
= y(x)
і позначається:
- диференційована ф-ія змінної х, то
диференціал цієй функції називається
другим диференціалом функції y
= y(x)
і позначається:





 диференційована
в точці внутрішнього екстремума
x
∈ D
то
f’(x)
= 0.
диференційована
в точці внутрішнього екстремума
x
∈ D
то
f’(x)
= 0. > 0,
існує б
> 0 : ∀ |Δx|
< б ⇒ |α(Δx)|
< ε
, тоді
для всіх |Δx|
< б
sign
(f’(x0)
+ α(Δx))
= sign
f’(x0)
і
(f’(x0)
+ α(Δx))*Δx
змінює
знак разом зі зміною знака
Δx.
Разом
з цим добутком міняє знак і різниця
f(x)
– f(x0),
що не можливо якщо точка x0
це точка екстремума ⇒
припущення хибне, отже f’(x0)
= 0
> 0,
існує б
> 0 : ∀ |Δx|
< б ⇒ |α(Δx)|
< ε
, тоді
для всіх |Δx|
< б
sign
(f’(x0)
+ α(Δx))
= sign
f’(x0)
і
(f’(x0)
+ α(Δx))*Δx
змінює
знак разом зі зміною знака
Δx.
Разом
з цим добутком міняє знак і різниця
f(x)
– f(x0),
що не можливо якщо точка x0
це точка екстремума ⇒
припущення хибне, отже f’(x0)
= 0 Перевіримо, що для функції F(x) виконані
всі умови теореми
Ролля. І
справді, F(x) неперервна
на проміжку [a;b] (як
різниця функції f(x) та
лінійної функції) та в усіх внутрішніх
точках проміжка [a;b] має
похідну:.
Перевіримо, що для функції F(x) виконані
всі умови теореми
Ролля. І
справді, F(x) неперервна
на проміжку [a;b] (як
різниця функції f(x) та
лінійної функції) та в усіх внутрішніх
точках проміжка [a;b] має
похідну:.
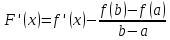 З формули (1) очевидно, що F(a)
= F(b)
= 0.
З формули (1) очевидно, що F(a)
= F(b)
= 0.
 Перевіримо, що для функції F(x) виконані
всі умови теореми
Ролля. І
справді, F(x) неперервна
на проміжку [a;b] (як
різниця функції f(x) та
лінійної функції) та в усіх внутрішніх
точках проміжка [a;b] має
похідну:.
Перевіримо, що для функції F(x) виконані
всі умови теореми
Ролля. І
справді, F(x) неперервна
на проміжку [a;b] (як
різниця функції f(x) та
лінійної функції) та в усіх внутрішніх
точках проміжка [a;b] має
похідну:.
 З формули (1) очевидно, що F(a)
= F(b)
= 0.
З формули (1) очевидно, що F(a)
= F(b)
= 0.
 невідємна
(додатна), то f(x)
– не спадна (зростаюча) на
[a;b]
Доведеня
Нехай
невідємна
(додатна), то f(x)
– не спадна (зростаюча) на
[a;b]
Доведеня
Нехай
 виконані
умови теореми Лагранжа
виконані
умови теореми Лагранжа
 Аналогічно
отримуєм, якщо f’(x)
< 0 ,
Аналогічно
отримуєм, якщо f’(x)
< 0 ,
 то f(x)
– не зростаюча (спадна)
то f(x)
– не зростаюча (спадна)



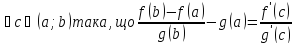 Доведення
Розглянемо
допоміжну
функцію
Доведення
Розглянемо
допоміжну
функцію


 =>
=>



 Тоді
Тоді


 – довільний
многочлен n-го
порядку.
Запишемо у вигляді:
– довільний
многочлен n-го
порядку.
Запишемо у вигляді:
 Щоб знайти С, підставимо замість x
= x0
Щоб знайти С, підставимо замість x
= x0


 Методом математичної індукції
Методом математичної індукції

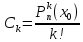 ,
k
= 0,1…n;
,
k
= 0,1…n;
 +
+ Якщо
Якщо
 або тільки в т. х0,
то їй відповідає многочлен
або тільки в т. х0,
то їй відповідає многочлен
 Цей многочлен називається многочленом
тейлора функції f(x)
в т. х0
і пов'язаний з функцією f(x)
тим, що його значення і значення всіх
його похідних до порядоку n
в т. х0
співпадають зі значенням функції та
її похідних в цій точці. Якщо позначити
через
Цей многочлен називається многочленом
тейлора функції f(x)
в т. х0
і пов'язаний з функцією f(x)
тим, що його значення і значення всіх
його похідних до порядоку n
в т. х0
співпадають зі значенням функції та
її похідних в цій точці. Якщо позначити
через
 то
то
 називається
формулою Тейлора
називається
формулою Тейлора