
ekzamen_шпора
.docx
|
46.Теорема про залишок формули Тейлора |
|
Якщо
на [a;b]
f(x)
– неперервна і
має (n+1)
похідну
на (a;b),
то для ∀g(x)
– диференційованої
на (a;b)
такої,
що g’(x) ≠
0, ∀x
∈ (a;b)
∃c
між
x
i
x0
:
|
|
Доведення
Розглянемо
функцію:
|
|
Формула
Тейлора з залишком в формі Лагранжа
|
|
47. Локальна теорема Тейлора |
|
Нехай
f(x)
- (n+1)
диференц.
на (a;b),
причому
∃M:
|f(n+1)(x)|
≤
M
∀x
∈ (a;b)
Тоді
∀x,
х0
∈
[a;b]
⇒
|
|
Доведення
Залишок
в формі Лагранжа має вигляд
|
|
48.Формула Тейлора для головних елементарних функція |
|
x0
= 0
1.
|
|
49. Необхідні та достатні умови локального екстремуму функції в термінах першої похідної |
|
необхідні
Для
того щоб точка x0
∈
(a;b)
була
точкою внутрішнього екстремума функції
|
|
Доведення
Якщо
x0
∈
(a;b)
точка екстремума
Точки в яких для f(x) виконано умови 1,2 називаються критичними точками f(x) |
|
достатні
Нехай
f(x)
– диферент.
в деякому проколотому околі U(x0),
x
– критична
для f(x)
Якщо
f’(x)
не
міняє знак при переході через т. х0
то в т. х0
екстремума немає
∃б
>
0
|
|
Доведення
|
|
51. Достатні умови локального екстремуму функції за першою похідною |
|
Нехай
f(x)
– диферент.
в деякому проколотому околі U(x0),
x
– критична
для f(x)
Якщо
f’(x)
не
міняє знак при переході через т. х0
то в т. х0
екстремума немає
∃б
>
0
|
|
Доведення
|
|
52. Достатні умови локального екстремуму функції в термінах вищих похідних |
|
Нехай
f(x)
визначена
в деякому U(x0)
при
чому
|
|
Доведення
За
теоремою Тейлора
|
|
53. Опуклі функції, різновиди означення опуклості |
|
Функція
|
|
Переформулювання
визначення опуклості
Позначимо
через х = (1-a)x1
+ ax2
= x1
+ a(x2-x1).
Виразимо
a
через
х
|
|
55. Опуклі функції, точки перегину. Умови існування точки перегину. |
|
Якщо
|
|
Тверждення Якщо
|
|
доведення х0-
точка перегину f(x)=> за критерієм
опуклості
Достатня
умова точки перегину є зміна знаку
|
|
54.Критерій опуклості диференційованих функцій |
|
Диференційована на (a;b) функція f: (a;b)R опукла на (a;b) її похідна монотонна на (a;b). При цьому, не спаданню функції відповідає опуклість вниз, а незростанню – опуклість вверх. Строгій монотонності похідної відповідає строга монотонність. |
|
доведення Нехай, для визначеності, розглянемо випадок опуклої вниз функції. (=>)
f(x) – опукла вниз => (з нерівності 2
Тоді
З
іншого боку, якщо xx2,
то
Для
f(x) виконані умови теореми Лагранжа,
а значить,
Аналогічно,
для вверх отримуємо, що
(<=)
Нехай f(x)-диференційована
на (a;b):
Аналогічно,
для зростаючої функції
Випадок
строгої монотонності: якщо
|
|
Наслідок Якщо
Якщо
Якщо
Якщо
|
|
56. Нерівність Йенсена. Наслідок з неї |
|
Якщо
f: (a;b)
R опукла вверх (вниз) на (a;b), то для
|
|
Доведення За методом ММІ: n=2
Нехай
для n-1 виконується, тоді для n – маємо:
Нехай
для визначеності
Позначимо
|
|
Наслідок З
доведення видно, що якщо
|
|
57. Асимптоти графіка функції. Схема побудови гр.функції. |
|
Пряма l називається асимптотою кривої на координатній площині, якщо відстань від точок M(x;y) з кривої до прямої l прямує до 0 за умови M(x;y) 0. І. Вертикальні асимптоти Це прямі, рівняння яких має вигляд х=х0. Тоді, для графіка функції y=y(x) пряма х=х0 буде асимптотою тоді і тільки тоді, коли:
Це означає, що вертикальні асимптоти для графіка функції y=y(x) можуть бути тільки в точках розриву ІІ роду, або на границі обл. визначення. |
|
ІІ. Горизонтальні асимптоти Горизонтальні ас-ти – прямі l: y=b
M(x,y)∞
x±∞
і умова
|
|
ІІІ. Вертикальні асимптоти Прямі, що задаються рівнянням y=kx+b M(x,y)∞ x±∞ d(M(x,y);l)=|MM2|=|MM1|*sinφ =>d(M,l)=|MM2|0 |MM1| 0. |MM1|=|y(x)-l(x)|=|y(x)-kx-b|0 тоді
|
|
Теорема l: y=kx+b буде асимптотою для графіка функції y=y(x) тттк
|
|
доведення (=>)
y=kx+b – асимптота, тоді
Із
умови
(<=)
дано:
|
|
Схема побудови графіка. Область визначення; Парність/непарність, періодичність; Точки перетину з осями координат; Інтервали неперервності, точки розриву, асимптоти; Дослідження за допомоги першої похідної – монотонність; Дослідження за допомогою другої похідної – опуклість; Наносимо на координатну площину характерні точки, точки перегину, асимптоти, будуємо ескіз графіка. |
|
58. Первісна та невизначений інтеграл. Таблиця інтегралів. |
|
F(x)
називається первісною функції f(x) на
(а;б) якщо
|
|
Теорема |
|
Якщо F(x) якає первісною для f(x) на (a;b) то для будь-якої іншої її первісної Ф(х) на (a;b) існує константа така, що Ф(х)= F(x)+С. І навпаки, для будь-якої константи: Ф(х)= F(x)+C буде первісною f(x). |
|
Доведення 1.
Ф(х),
F(x) – первісні f(x) =>для H(x)= Ф(х)- F(x),
маємо:
|
|
Визначення Множина
всіх первісних f(x) на (a;b) називається
невизначеним інтегралом від f(x) на
(a;b) і позначається
|
|
Таблиця інтегралів
|
|
59. Властивості невизначеного інтегралу |
|
Якщо
|
|
доведення За
властивостями похідних, похідна
За властивостями похідних, доведення аналогічно до 3. Заміна
змінних: якщо на деякому проміжку
(a;b)
|
|
доведення За
формулою похідної складної функції
маємо:
|
|
Зауваження За
властивістю 5 => якщо Якщо
= |
|
Інтегрування за частинами
З властивостей диференціалів: d(uv)=udv+vdu=> udv = d(uv) – vdu =>
|
|
60. Інтегрування раціональних дробів |
|
|
|
Інтегрування найпростіших
|
|
В загальному випадку теорема Якщо
дріб То
дріб
|
|
61.Інтегрування тригонометричних виразів. |
|
Нехай R(sin x,cos x) -- раціональний вираз змінних sin x,cos x((sin аx,cos аx)!) |
|
1.Універсальна тригонометрична підстановка |
|
t=tg( cos
x = x=arctg(tg |
|
a)Якщо R(-sin x,-cos x) = R(sin x,cos x) => може допомогти підстановка t= tgx або t=ctg x cos^2(x)
= |
|
б) R(sin x,cos x)= cosmx * sinnx Можливі випадки: 1) m - непарне (2к+1) => cosmx sinnx dx=(cos2kx*sinnx*cosx)dx=(1-sin2(x))ksinnxd(sinx)={t=sin x}=(1-t2)tndt 2) n-непарне (2к+1) => cosmx*sinnx=cosmx*sin2kx*sinx dx = 1-cosmx(1-cos2x)k d(cosx)={t=cos x}= -tm(1-t2)kdt 3)m,n
-- парні;
m=2k;
n=2l => sin x*cosx = 4) sina *cosb=1/2(cos(a+b)+sin(a-b)); cosa*cosb=1/2(cos(a+b)+cos(a-b)) sina*sinb=1/2(cos(a-b)-cos(a+b)) |
|
63. Нескінченно великі. Їх влст. |
|
1)f(x),
g(x)
-- неск.
великі
при х
->а
|
|
2)Якщо
f(x)
- н.в. при х
->а
|
|
3)
f(x),
g(x)
-- неск.
великі
при х
->а
|
|
4)якщо
f(x)
- н.в., а g(x)
така що
f(x)*g(x)
- н.в. при х
->а
|
|
Зв'язок н.в. і н.м. |
|
якщо
f(x)
-- н.в. ,а α(x)
-- н.м.
при
х
->а
|
|
Заув. Якщо f(x) -- н.в. ,а α(x) -- н.м. при х ->а; f(x)* α(x) -- може бути яким завгодно |
|
62.Інтегрування ірраціональних виразів |
|
1)Якщо підінтегральна фунція містить різні корені даного виразу заміна => ax+b=tN, N-підбирається Або
|
|
|
|
Диф. Біном
Вираз під інтегралом – це диф.біном(m,n,p – раціональні числа) 1)p-ціле, підстановка x=tN,де N таке щоб добувалися корені заховані в n |
|
Приклад:
2)m+1/n=1/4 не ціле 3)m+1/n+p=0 ціле
|

 , ∀x,x0
∈ [a;b]
, ∀x,x0
∈ [a;b] при фіксованих
x0
i
x.
при фіксованих
x0
i
x.
 ;
;
 ⇒
⇒
 ;
;
 , ⇒
Для функції
F(t)
i
g(t)
виконані
умови теореми Коші ⇒
між x0
i
x
∃c
таке
що:
, ⇒
Для функції
F(t)
i
g(t)
виконані
умови теореми Коші ⇒
між x0
i
x
∃c
таке
що:
 ⇒
⇒


 формула
Тейлора з залишком у формі Пеано.
формула
Тейлора з залишком у формі Пеано. =
=
 o
o
 =
=
 ⇒
⇒

 2.
2.
 3.
3.
 4.
4.
 5.
5.
 Доведення
Доведення
 1.
1.
 ⇒
∀k
⇒
∀k
 ⇒
∀k
⇒
∀k
 2.
2.
 ⇒
∀k
⇒
∀k
 ⇒
∀k
⇒
∀k
 3.
3.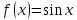 ⇒
∀k
⇒
∀k
 ⇒
∀k
⇒
∀k
 4.
4.
 ⇒
⇒
 ⇒
∀k
≥
1
⇒
∀k
≥
1
 5.
5.
 ⇒
⇒
 ⇒
⇒
 ⇒
⇒

 – необхідне
виконання однієї з двох умов
1. f(x)
– недиференційована
в т. x0
2. f’(x)
= 0;
– необхідне
виконання однієї з двох умов
1. f(x)
– недиференційована
в т. x0
2. f’(x)
= 0; ,
то можливі два випадки: 1. f(x)
– недиференційована
в т. x0
– виконана умова. 2. f’(x)
диференційована
в т. x0
тоді за теоремою Ферма f’(x0)
= 0 ⇒
виконана
умова 2.
,
то можливі два випадки: 1. f(x)
– недиференційована
в т. x0
– виконана умова. 2. f’(x)
диференційована
в т. x0
тоді за теоремою Ферма f’(x0)
= 0 ⇒
виконана
умова 2. Якщо
f’(x)
міняє
знак через т. х0
тобто
∃б
>
0
Якщо
f’(x)
міняє
знак через т. х0
тобто
∃б
>
0
 то
в т.
х0
екстремум є, при чому якщо
то
в т.
х0
екстремум є, при чому якщо
 ,
,
 - т.
х0
екстремума, якщо
- т.
х0
екстремума, якщо
 ,
,
 - т.
х0
максимума
- т.
х0
максимума ,
,
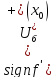 ⇒
на інтервалі (x0
- б;
х) f(x)
спадає,
а
на інтервалі (x0;
x0+б)
– зростає ⇒
f(x0)
= inf
f(x),
x
є (x0
- б;
х), f(x0)
= inf
f(x),
x
є (x0;
x0+б)
⇒
f(x0)
= min
f(x)
– локальний
мінімум,
x
є (x0
- б;
x0+б)
анагалогічно
⇒
на інтервалі (x0
- б;
х) f(x)
спадає,
а
на інтервалі (x0;
x0+б)
– зростає ⇒
f(x0)
= inf
f(x),
x
є (x0
- б;
х), f(x0)
= inf
f(x),
x
є (x0;
x0+б)
⇒
f(x0)
= min
f(x)
– локальний
мінімум,
x
є (x0
- б;
x0+б)
анагалогічно ,
,

 Якщо
f’(x)
міняє
знак через т. х0
тобто
∃б
>
0
Якщо
f’(x)
міняє
знак через т. х0
тобто
∃б
>
0
 то
в т.
х0
екстремум є, при чому якщо
то
в т.
х0
екстремум є, при чому якщо
 ,
,
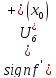 - т.
х0
екстремума, якщо
- т.
х0
екстремума, якщо
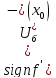 ,
,
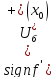 - т.
х0
максимума
- т.
х0
максимума ,
,
 ⇒
на інтервалі (x0
- б;
х) f(x)
спадає,
а
на інтервалі (x0;
x0+б)
– зростає ⇒
f(x0)
= inf
f(x),
x
є (x0
- б;
х), f(x0)
= inf
f(x),
x
є (x0;
x0+б)
⇒
f(x0)
= min
f(x)
– локальний
мінімум,
x
є (x0
- б;
x0+б)
анагалогічно
⇒
на інтервалі (x0
- б;
х) f(x)
спадає,
а
на інтервалі (x0;
x0+б)
– зростає ⇒
f(x0)
= inf
f(x),
x
є (x0
- б;
х), f(x0)
= inf
f(x),
x
є (x0;
x0+б)
⇒
f(x0)
= min
f(x)
– локальний
мінімум,
x
є (x0
- б;
x0+б)
анагалогічно ,
,

 ,
а
,
а
 .
Тоді якщо n=2k+1
то
в
т. x0
екстремума
немає.
Якщо
n
= 2k
то
в
т. x0
екстремум
є, при чому якщо
.
Тоді якщо n=2k+1
то
в
т. x0
екстремума
немає.
Якщо
n
= 2k
то
в
т. x0
екстремум
є, при чому якщо
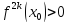 то
т.
x0
– min,
то
т.
x0
– min,
 то
т.
x0
– max
то
т.
x0
– max
 ⇒ ∃б
>
0
⇒ ∃б
>
0
 множник
множник
 зберігає знак
зберігає знак
 Тоді
у випадку n=2k+1,
Тоді
у випадку n=2k+1,
 міняє
знак при переході через х0
разом
з (x-x0)
⇒
різниця
міняє
знак при переході через х0
разом
з (x-x0)
⇒
різниця
 міняє
знак при переході через х0
⇒
в т. х0
екстремума немає.
При n
= 2k,
міняє
знак при переході через х0
⇒
в т. х0
екстремума немає.
При n
= 2k,
 різниця
різниця
 зберігає знак, причому якщо
зберігає знак, причому якщо
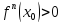 ⇒
⇒

 т. min,
якщо
т. min,
якщо
 ⇒
⇒

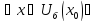 т. max
т. max називається
опуклою вниз (вверх) на цьому інтервалі
якщо
називається
опуклою вниз (вверх) на цьому інтервалі
якщо
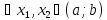 i
i
 має
місце
має
місце
 опукла
вниз
опукла
вниз
 ,
графік
функції знаходиться під хордою
опукла
вверх – графік функції знаходиться
над хордою
,
графік
функції знаходиться під хордою
опукла
вверх – графік функції знаходиться
над хордою .
Таким чином нерівність приймає вигляд
.
Таким чином нерівність приймає вигляд


 ; x2
– x1
> 0; x
– x1
> 0; x2
– x
> 0;
; x2
– x1
> 0; x
– x1
> 0; x2
– x
> 0;
 Визначення
2
f(x)
опукла вниз (вверх) на інтервалі (a;b)
якщо
Визначення
2
f(x)
опукла вниз (вверх) на інтервалі (a;b)
якщо
 і
і
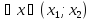 має місце
має місце
 Строгій нерівності, відповідає
строга опуклість
Строгій нерівності, відповідає
строга опуклість і x0 така, що на
і x0 така, що на
 і на
і на
 f(x) опукла різного характеру опуклості,
то точка х0 називається точкою перегину
f(x)
f(x) опукла різного характеру опуклості,
то точка х0 називається точкою перегину
f(x) на (a;b)
і х0
на (a;b)
і х0
 (a;b)
є точкою перегину f(x) то x0 є критичною
для
(a;b)
є точкою перегину f(x) то x0 є критичною
для
 .
. в цій точці міняє характер монотонності
=> це точка екстремума
в цій точці міняє характер монотонності
=> це точка екстремума
 => в цій точці
=> в цій точці
 не існує, або
не існує, або
 =0,
тобто, х0-критична для
=0,
тобто, х0-критична для
 .
. при переході через цю точку.
при переході через цю точку. )
)




 – неспадна
на (a;b).
Аналогічно показуємо, що в випадку
f(x) – опукла вверх =>
– неспадна
на (a;b).
Аналогічно показуємо, що в випадку
f(x) – опукла вверх =>
 – не зростаюча. Якщо f(x) – строго опукла
вниз, то маємо строгу нерівність(крім
того, що її похідна неспадна!):
– не зростаюча. Якщо f(x) – строго опукла
вниз, то маємо строгу нерівність(крім
того, що її похідна неспадна!):


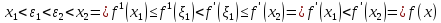 -зростаюча.
-зростаюча. -спадна
-спадна -
неспадна. Тоді
-
неспадна. Тоді


 отримуємо нерівність 2 зі знаком
отримуємо нерівність 2 зі знаком

 опукла
вверх.
опукла
вверх. - зростаюча, то отримуємо:
- зростаюча, то отримуємо:
 (a;b)
(a;b)
 опукла вниз на (a;b)
опукла вниз на (a;b) (a;b)
(a;b)
 опукла вгору
опукла вгору (a;b)
(a;b)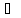
 опукла вниз на (a;b)
опукла вниз на (a;b) (a;b)
(a;b)
 опукла вгору на (a;b)
опукла вгору на (a;b) x1,x2,x3…xn
x1,x2,x3…xn
 (a;b) і для
(a;b) і для
 – невід’ємних, таких, що
– невід’ємних, таких, що
 має місце:
має місце: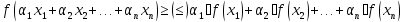

 – визначення
опуклості вверх (вниз).
– визначення
опуклості вверх (вниз).




 ,що
і треба було довести.
,що
і треба було довести. і f(x) строго опукла, то знак «=» в
нерівності Йенсена може бути лише в
випадку х1=х2=…=хn.
і f(x) строго опукла, то знак «=» в
нерівності Йенсена може бути лише в
випадку х1=х2=…=хn.

 0
0


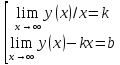



 =>
=> =>
y = kx+b – асим-а графіка функції. Аналогічно
доведення -∞.
=>
y = kx+b – асим-а графіка функції. Аналогічно
доведення -∞.
 За
наслідком з теореми Лагранжа - H(x)=С =>
Ф(х)- F(x)=C=> Ф(х)= F(x)+С
2.
За
наслідком з теореми Лагранжа - H(x)=С =>
Ф(х)- F(x)=C=> Ф(х)= F(x)+С
2.
 С
= const:
С
= const:
 - теж первісна для f(x)
- теж первісна для f(x) .
f(x) називається підінтегральною
функцією.
.
f(x) називається підінтегральною
функцією.






 і
і
 – диференційована функція
– диференційована функція
 ,
то
,
то

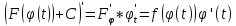
 ,
то
,
то

 ,
то
,
то


 ,
якщо
,
якщо
 – диференційовані.
– диференційовані.
 де
де
 - многочлени стемені M
i
N
відповідно.
Найпростіші
дроби
- многочлени стемені M
i
N
відповідно.
Найпростіші
дроби
 ;
;
 ;
;
 ;
;






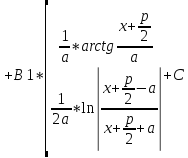
 -
правильна, тобто m<n
і знаменник розкладено на множники,
тобто
-
правильна, тобто m<n
і знаменник розкладено на множники,
тобто
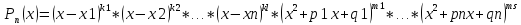 .
. розпадеться на суму найпростіших.
розпадеться на суму найпростіших.
 )
=> sin x =
)
=> sin x =
 =
=

 =
=

 ))
=> 2arctg t => dx=
))
=> 2arctg t => dx= (-π<x<π) =>
(-π<x<π) => ;
;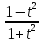 )
)
 =
=
 ;
sin x =
;
sin x = =
= ;
dx=
;
dx=
 sin2x;
cos2x=
sin2x;
cos2x= ;
sin2x=
;
sin2x=
 sin(cx+b)dx
=>застосовуємо
ф-ли перетворення добутку в суми:
sin(cx+b)dx
=>застосовуємо
ф-ли перетворення добутку в суми:
 одного
знаку, то f(x)+
g(x)
- н.в. при х
->а
одного
знаку, то f(x)+
g(x)
- н.в. при х
->а

 ,
а g(x)--
локально обмежена при х
->а
,
а g(x)--
локально обмежена при х
->а
 ,
то f(x)+
g(x)
= н.в.
,
то f(x)+
g(x)
= н.в. f(x)*g(x)=
н.в. при х
->а
f(x)*g(x)=
н.в. при х
->а

 М>0
і
М>0
і
 u0(a):
g(x)
u0(a):
g(x) М,
М,
 x
x u0(a),
то
u0(a),
то
 ,
то
,
то
 = н.м. , а
= н.м. , а
 - н.в.
- н.в.
 =tN
=tN



 m=0,n=4,p=-1/4
– не ціле.
m=0,n=4,p=-1/4
– не ціле. ;
;
