§2. Description of the vector field

2.1 Electric flux

Let us say, the fluid motion is characterized by the velocity vector field. The volume of fluid flowing per time unit through a certain cross-section S, is called a flow of liquid through the surface. To determine the flow, we need to divide the surface into elementary sections ∆S.

Consider the electric-field of the vector. We assume that the density of field lines is equal in magnitude to the electric-field vector itself, and then the number of lines, which permeate elementary plane dS will be evaluated, as a product EdScosα (normal line n to the surface will be at an angle α with the vector Е). This is the flow dФ of the vector Е through the plane dS.

fig.2.1

, (2.1)

S

Г

Е_n – projection Е onto the normal n, dS – vector whose magnitude is numerically equal to dS, and the direction coincides with the direction of the normal to the plane. The normal can be directed to both sides.

If there is a freeform surface, the flow is determined by integrating

. (2.2)

E

S α n

En

fig. 2.2

A flux of the vector E is algebraic value which depends on the choice of direction of the normal n and the configuration of the electric-field vector pattern.

2.2. Gauss’s theorem

Let us write the Gauss’s theorem, which in some cases simplifies evaluating of the electric field: electric vector flux through a closed surface equals to the algebraic sum of the charges contained within this surface, divided by ε₀:

. (2.3)

Proof:

Consider single charge field Q. Let us say, this charge is located inside a closed surface S (Fig.2.3).

Consider the vector flux through some element dS.

(dω =4π).

The value ,dω – angle, which is subtended on this surface with the vertex at the point where the charge Q is located.

fig.2.3

.

The integration over the area S is identical to the integration over the corner ω. After the integrating, we obtain:

.

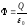When an electric field is created by a system of charges Q₁, Q₂, Q₃,... on the principle of superposition of fields, we have:

Then the electric flux is:

If the charge is located inside a closed surface, it is numerically equal to and it is equal to zero if located outside the surface.

Let us say, the charge is uniformly distributed over the volume V. Each elementary volume dV contains a point charge equal to ρdV and then on the right side of formula (3) we obtain:

. (2.4)

We make the integrating (2.4) only over the volume, which is located inside a closed surface.

At the time when the field of electric intensity itself depends on the configuration of all the charges, the flow E through a closed surface S is evaluated only by the algebraic sum of the charges within S, which means that if the charges move, the field with strength E changes everywhere and the vector through the given area S also changes. But, if the movement of the charge happens without crossing the surface S, then the flow through a given surface remains unchanged, although the field strength may change and quite substantially.

2.3. Divergence of electric-field vector

In order to determine the divergence of electric-field vector, we need to define the differential form of Gauss’s theorem and to find the relationship between the volumetric charge density and the charge distributed in this volume.

Let us imagine the charge in a volume V surrounded by a closed surface S. The inner charge Q is determined from the formula:

Q_inner=<ρ>V,

where <ρ> − volume charge density, average over the value.

Let us substitute this expression into the equation of Gauss’s theorem (2.3):

. (2.5)

Let’s direct this volume to zero by pulling it to the point of the field, which we are interested in. Obviously, in this case <ρ> will follow up to the value ρ at this point. Consequently, the ratio of the left side (2.5) will tend to .

The value which is the boundary of ratio 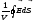is calleddivergence of the electric field Е.

. (2.6)

(2.7)

2.4. Ostrogradskiy-Gauss theorem

Knowing the divergence of the intensity vector in any point of space, we can find the flux of the vector E through any closed surface of finite size.

Now consider the flow velocity vector for an ideal fluid.

The product divV on dV gives the power to the source of fluid covered by a volume dV, the sum of the products gives the total algebraic power sources throughout the volume V, in which the integration: .

Due to the fact that the fluid is not compressed, the total power of the source surface is equal to the fluid flow, which flows outside through the surface S, which limits the volume V.

Thus, .

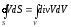This statement is a mathematical account of the theorem of Ostrogradskiy-Gauss.

This theorem is true for the vector field of any nature. Therefore we can write:

. (2.8)

2.5. Circulation and rotor of intensity vector

Now imagene a closed contour G, through which an ideal fluid is moving (fig.2.4). Freeze instantly fluid in the entire volume except for a thin closed channel of constant cross section, which includes the contour G. Depending on the nature of the field of velocity vector, the fluid in the channel is either stationary or will circulate along this contour.

As a measure of this movement we will take the value – the product of the velocity on the length of the contour; the circulation of the velocity vector along the contourG.

circulation V on G = Vl

Since the channel has a constant cross section, V=const, at a time when there was a solidification of the walls. Each of the particles of the fluid in the channel will retard the velocity of the component, perpendicular to the wall and the only component of velocity tangent to the contour – V_l (tangential component) will remain. This component is related to the elementary impulse dp_i, module of which for a particle of fluid that is on a segment of the channel dl, has a value , whereρ – density of the of the fluid, σ - is the cross - sectional area of the channel.

Since the fluid is ideal, the effect of the walls can vary only along dp_i, but does not affect its value. Thus the algebraic sum of the impulses can not change, that is, impulse gained by one of the particles is numerically equal to the impulse that is lost by another particle, i.e.:

,

Where V – velocity of circulation, V_i – tangential component of the fluid velocity in the volume before solidification of the walls of the channel. By reducing the value onρ and σ we recive:

circulation .

Similarly defines a circulation of any vector by an arbitrary closed contour is defined. Then:

circulation .

If we consider the laminar fluid flow in the river, the velocity at the bottom is zero and gradually increases when approaching the surface of the water and the line of the velocity vector will be rectilinear. However, in the field of curved lines circulation may be zero.

The circulation of the vector is characterized by the properties of the fields, which have the average values over the surface. To obtain the average values at the point P, it is necessary to reduce the size of the contour G and respectively, to decrease the circulation and size of the contour.

The ratio of the circulation of the vector to the surface S is directed to some boundary that used to characterize the field at point R.

Take the contour G, which lies in a plane that passes through the point P and consider the expression:

,

where S – area covered by the contour G. For an arbitrary plane this limit is not possible to determine the characteristic of the field at the point P, because it depends not only on the point P, but also on the orientation of the contour in space. This orientation can be set to the positive direction of the normal n to the area of counter G. Normal is considered positive when it is related to the direction of the countour traversing under the integration rule by right screw.

Determining the normals (2.10) in one point P for different directions of we will get different values, and for opposite directions n, they differ only in their signs. For same direction value n (2.10) at this point will be maximum. Thus, the ratio (2.10) behaves as a projection of the vector in the n direction. The maximum value (2.10) defines a module of the vector and the positive direction of the normal, at which the maximum is reached gives the direction of the vector. This vector is called the rotor, or curl of vector V and is denoted as:

.

–the projection of the vector on the positive normal to theS, covered by the contour G.

In places where the rotor is different from zero, the mill is moving with a greater velocity, more than the projection of the rotor on the axis of this mill.