3.3 The field of two parallel charged planes

Presume that each of the planes is equal in magnitude but different in sign to the surface charge density σ.

The field of two charged surfaces can be found as a superposition of fields generated by each plane separately. Between the planes, tension fields are added and they have the same direction, i.e.:

.

In this formula σ - is the module of surface charge density.

The field in this case is between the planes and is homogeneous in this area. The result is true for plane of finite size, if the distance between the planes is much smaller than the area of the planes (plate capacitor).

The most noticeable deviations of homogeneity exist only near the plates, but they are negligible.

4. The field of the infinite round cylinder

Presume that, the field is created by infinite cylindrical surface with R radius and this surface is charged by constant surface density σ. For the symmetry reasons intensity of the a field in any point is directed along a straight line, which is perpendicular to the axis of the cylinder. The magnitude voltage doesn't depend on r distance from a cylinder axis.

Imasine some coaxial closed cylindrical surface of radius of r and h length.

i For the base of cylinder E_n=0. Intensity of electric field, in this case, is perpendicular to the cylinder surfaces.

For a lateral surface of the cylinder E_n=E(r).

We will consider a charge positive.

From this follows that stream Е through a lateral surface numerically is equal .

E

R ᵪ r

h

fig 3.4

If this radius r>R, all charge of Q will get in this surface, which - numerically will be equal to the production of the linear density of this charge and cylinder h length.

Q=τh,

(τ – linear density of a charge).

We use Gauss's theorem:

;

. (3.3)

The formula (3.3) is true at r ≥R.

If r<R, then unbounded surface lack in charge, as a result Е(r)=0.

Thus, in side evenly charged cylindrical surface of infinite length the field is absent. Intensity, from the outside of a surface is defined by the linear density of τ and r distance from a cylinder axis.

The field of negatively charged cylinder differs from the a field of positively charged cylinder only in the direction of a vector of intensity, but not its size..

From the formula (3.3) it follows that by reducing cylinder radius R, at uniform linear density of a charge, it is possible to receive a field with very big intensity near a cylinder surface. Having substituted (3.3) in a condition, that and having presented thatr=R, we will receive, for intensity of a field, directly at a cylinder surface

. (3.4)

By means of the principle of superposition, it is possible to find a field of two coaxial cylindrical surfaces with identical in size, but different in a sign, linear density τ. Then, the field lies between surfaces.

In smaller and outside of bigger cylinders, the field is absent, and between cylinders tension's size is denoted by formula (3.3).

It is also true for cylindrical surfaces of finished length if the distance between surfaces is much less than their length (the cylindrical capacitor). Deviation are noticeable - only near edges of the cylinder.

fig. 3.5

3.5.The field of spherically charged surface

The field created by a spherical surface of radius of R, which is loaded with area density σ will be centrosymmetric. That is, the direction of dencity vector in any point passing through the center of the sphere is a function of distance of R from the sphere center.

Imagine a concentric surface of radius in this surface r.

For all points of this surface E_n=E(r).

If r>R –the whole charge of Q will get distributed on a surfaces of the sphere and therefore it is possible to write Gauss's theorem:

.

From this equation

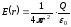, (r ≥R). (3.5)

The spherical surface of radius r which is less than R will not have charges, owing to what for the case of r<R

Е_n(r)=0.

Thus in a spherical surface with constant surface density - the field is absent, from the outside of this surface the field is identical with the field of a dot charge of the same size placed in the center of the sphere.

Using the principle of imposing of fields, it is possible to show that the field of two spherical surfaces which have identical charges, but with opposite signs, will be in an interval between surfaces, and the size of intensity will be determined by a formula Е.

3.6.The field of volumetrically charged sphere

Let the sphere R be charged with a constant volume density of a charge ρ. The field, in this case, possesses the central symmetry.

For a field outside of a sphere, we have the same result as for a spherical surface - the equation (3.5). But, for points inside a sphere – the result is

different.

Spherical surface (r<R) comprises a charge

.

Therefore Gauss's theorem for such surface will look like:

.

Volume charge density . We will insert this value into the previous formula. Then:

, (r≤R).

Thus, inside the sphere intensity increases linearly with r distance towards the center, and outside of the sphere it reduces with the increase in distance of r.

fig. 3.6 fig. 3.7

r E

R

E=0

r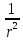

r

Lecture 4

Part 2. Dielectric in external electric field