Приклади розв’язання заданих задач Розв’язок завдання №1

Рівняння системи:

Локалізація коренів:

Перше рівняння, вирішене відносно x2:

Друге рівняння, вирішене відносно x2:

Перший корінь:

Початкове приближення:

Точність для блока Given Find:

TOL:=

Решення системи f(x1,x2)=0 за допомогою вбудованого блока MATHCAD:

Given

0

0

Find(

Отримане приблизне розв’язок:

Контрольні питання

1. Постановка задачі розв’язок нелінійних рівнянь. Основні етапи розв’язання задачі.

2. Метод простої ітерації: опис методу, умова і швидкість збіжності, критерій закінчення, зведення до вигляду, зручному для ітерацій.

3. Метод Ньютона: опис метод, теорема про збіжність, критерій закінчення.

4. Недоліки методу Ньютона. Модифікації методу Ньютона.

5. Метод диференціювання по параметру.

6. Застосування методів розв’язання систем нелінійних рівнянь для задачі мінімізації функцій.

7. Вирішити методом Ньютона з точністю системи рівнянь:

a) ,

b) ,

8. Розв’язати методом простої ітерації наступні системи:

a) ,

b) ,

9. Для функції знайти точки мінімума, зводжуючи задачу до розв’язку системи рівнянь.

Комп’ютерний практикум 6

Тема: Наближення функцій (Інтерполяція).

Мета: Вивчення основних визначень та положень теорії інтерполяції функції. Визначення особливостей інтерполяції функцій многочленами Лагранжа та Ньютона, сплайн-інтерполяції. Порівняння якості приближення функцій різними методами за умови різного розподілу і кількості вузлів інтерполяції.

Загальні положення

Інтерполяційний многочлен Лагранжа в загальному випадку має вигляд: , де– коефіцієнт полінома Лагранжа. При цьому його залишковий член матиме наступний вигляд:, де.

Інтерполяційний многочлен Ньютона в загальному випадку виглядає наступним чином: , де,a коефіцієнти є різничним відношенням функції. Тому для їх знаходження можна використати формулу для різничних відношень. В даному випадку залишковий член матиме такий же вигляд, як і в попередньому.

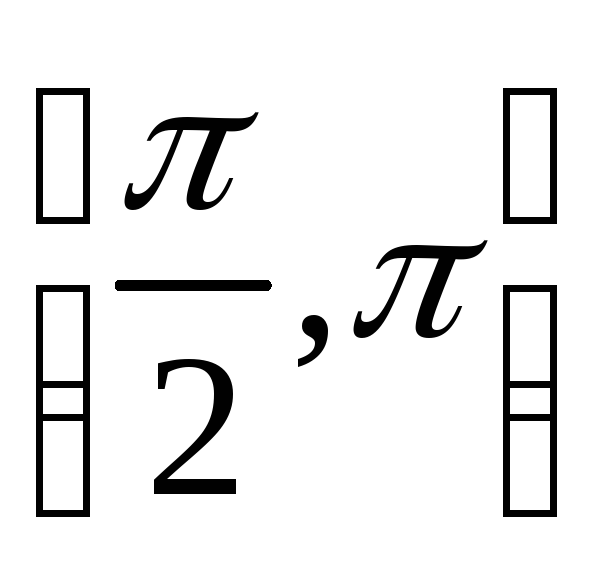
Формула розподілу Чебишевських вузлів на проміжку :

.

Кусково-лінійна інтерполяція являє собою так звану інтерполяцію лінійними сплайнами. В загальному вигляді формула для даного методу

матиме наступний вигляд: , де, при. Її також можна переписати наступним чином:

Функція називається кубічним сплайном, якщо існуєкубічних поліномівз коефіцієнтамита , які задовольняють наступним умовам:

Де

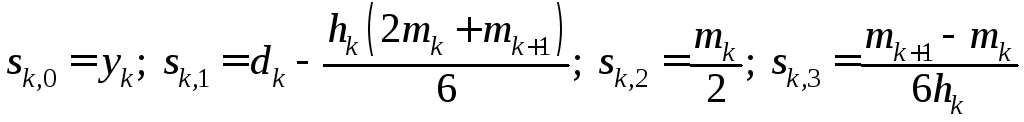
_{Таблиця 6.1 - Обмеження в граничних точках для кубічного сплайна}

_{Опис стратегії Рівняння відносно m0 і mN}

Робоче завдання

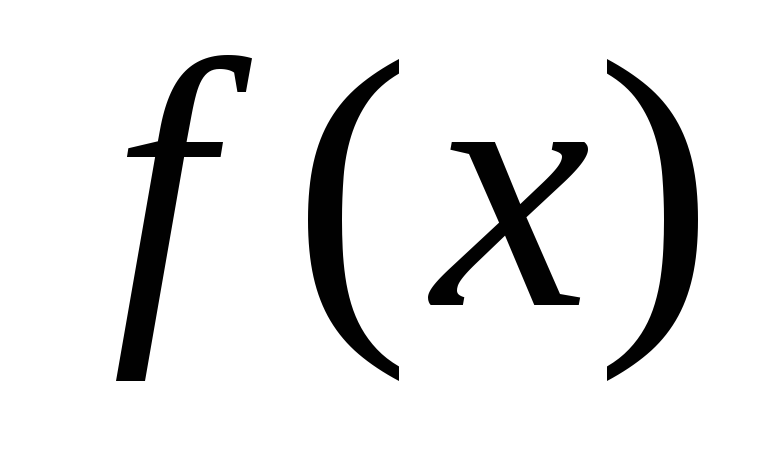1. Дана функція(Табл. 6.1) Приблизитина проміжку [a;b] інтерполяційними многочленами Лагранжа та многочленами Ньютона. На одному рисунку побудувати графіки приближуючих многочленів та функції . Для многочлена 3 степені порівняти якість приближення при різному виборі вузлів інтерполяції

2. Дана кусково-гладка функція на проміжку[a;b]. Порівняти якість приближення функції кусково-лінійною інтерполяцією та інтерполяційним многочленом Лагранжа

3. Дана функція. Приблизити на проміжку методом Ньютона при рівномірному та Чебишевському розподілі вузлів інтерполяції. Порівняти якість приближення.

4. Дана функція. Приблизити на проміжку методом Ньютона та кубічним сплайном (для кожного члена бригади з різними граничними умовами). На одному рисунку побудувати графіки приближуючої функції та функції . Порівняти якість приближення при різній кількості вузлів інтерполяції.

Таблиця 6.2 - Завдання1

N		N		N
6.1.1		6.1.2		6.1.3
6.1.4		6.1.5		6.1.6
6.1.7		6.1.8		6.1.9
6.1.10		6.1.11		6.1.12
6.1.13		6.1.14		6.1.15

Таблиця 6.3 - Завдання2

N		N		N
6.2.1		6.2.2		6.2.3
6.2.4		6.2.5		6.2.6
6.2.7		6.2.8		6.2.9

Таблиця 6.4. Завдання 3

N		N		N
6.3.1		6.3.2		6.3.3
6.3.4		6.3.5		6.3.6
6.3.7		6.3.8		6.3.9

N		N		N
6.4.1		6.4.2		6.4.3
5 ∙sin(x2)	[0,4] s1’=2 s2’=1	3∙sin(x3)	[1,2.5]	7∙ех∙sin(х2)	[0,4]
змикаючий		екстраполяційний		природній
6.4.4		6.4.5		6.4.6
6sin(x) x	[5,15]	10cos(x3) x	[1,2.75] s1’’=7 s2’’=4	11sin(х3) х		[1,2.75] s1’=3 s2’=4
З постійною 2-ю похідною		З заданою 2-ю похідною		змикаючий
6.4.7		6.4.6		6.4.9
8∙еx∙cos(х2)	[1,3.75]	12sin(ex)	[1,1.28] s1’’=3 s2”=4	40cos(x3)		[3,3.5]
Екстраполяційний		З заданою 2-ю похідною		Екстраполяційний
6.4.10		6.4.11		6.4.12
110sin(х3) x	[3,3.5]	х2cos(x)	[0,5]	10 cos(х) x		[3,5]
З постійною 2-ю похідною		природній		З постійною 2-ю похідною
6.4.13		6.4.14		6.4.15
9cos(ex)	[1,1.28] s1’=5 s2’=4	ecos(3x)	[0,4]	хsin(х2)		[0,5]
змикаючий		Екстраполяційний		природній

Таблиця 6.5. Завдання 4