Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Казанский государственный архитектурно-строительный университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

сборник задач по динамике

.pdf

Скачиваний:

205

Добавлен:

17.03.2016

Размер:

1.79 Mб

Скачать

☆

1 / 41 2 3 4 > Следующая >>>

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

КАЗАНСКИЙ ГОСУДАРСТВЕННЫЙ АРХИТЕКТУРНО-СТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТ

Кафедра механики

Сборник задач по динамике

для подготовки и защиты расчетно-графических работ

Методические указания для студентов всех направлений подготовки

и форм обучения

Казань

2015

УДК 531.3 ББК 22.213

	Г94
Г94	Сборник задач по динамике для подготовки и защиты расчетно-

графических работ: методич. указания для студентов всех направлений подготовки и форм обучения / сост. А.В. Гумеров, Ф.Г. Шигабутдинов. – Казань: Изд-во Казанск. гос. архитект.-строит. ун-та, 2015. – 39 с.

Печатается по решению Редакционно-издательского совета Казанского государственного архитектурно-строительного университета.

Методические указания предназначены для проведения практических занятий, оперативного контроля знаний на зачетах, при приеме расчетнографических работ, при допуске к экзамену и могут быть использованы студентами для самоконтроля.

Рецензент Кандидат технических наук, доцент кафедры МК и ИС КГАСУ

О.И. Ефимов

УДК 531.3 ББК 22.213

Казанский государственный архитектурно-строительный университет, 2015

Гумеров А.В., Шигабутдинов Ф.Г., 2015

1. ДИНАМИКА МАТЕРИАЛЬНОЙ ТОЧКИ

1.1. Законы динамики Динамикой называется раздел механики, в котором изучается движение

материальных тел под действием сил.

В основе динамики лежат законы, впервые сформулированные Ньютоном.

Закон инерции (первый закон). Материальная точка сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока какая-нибудь сила не выведет ее из этого состояния.

Если F 0, то v const .

Закон пропорциональности силы и ускорения (второй закон – основной закон динамики). Ускорение материальной точки пропорционально приложенной к ней силе и имеет одинаковое с ней направление (рис. 1.1), т.е.

					v
	ma F	,	m		v
	ma F	,	m
где m – коэффициент пропорциональности, характе-			a
ризует инертные свойства материальной точки и
				F
				F
называется массой точки.			Рис. 1.1

Закон равенства действия и противодействия (третий закон). Всякому действию соответствует равное и противоположно направленное

противодействие, т.е. F1 F2 .

Закон независимости действия сил (четвертый закон). Ускорение,

полученное точкой под действием системы сил, равно векторной сумме ускорений от действия отдельных сил, т.е.


				ma	Fk	.			(1.1)
1.2. Дифференциальные уравнения движения точки
Дифференциальные уравнения движения материальной точки в
декартовых координатах:
	mx	Fkx Fx ,	my		Fky Fy , mz		Fkz Fz	.	(1.2)

В проекциях на естественные оси – касательную, главную нормаль и бинормаль, получаем дифференциальные уравнения движения точки в проекциях на оси естественного трехгранника:

			md 2s dt2 F , mv2	Fn , 0 Fb	,	(1.3)
		, v ds dt , s – дуговая координата,
где v	v	, v ds dt , s – дуговая координата,		– радиус кривизны траектории.

Задачи динамики

1)Зная закон движения точки массой m определить действующую на нее силу (первая задача динамики).

2)Зная силы, действующие на материальную точку, ее массу m, а также начальные условия движения, определить закон движения точки (вторая задача динамики).

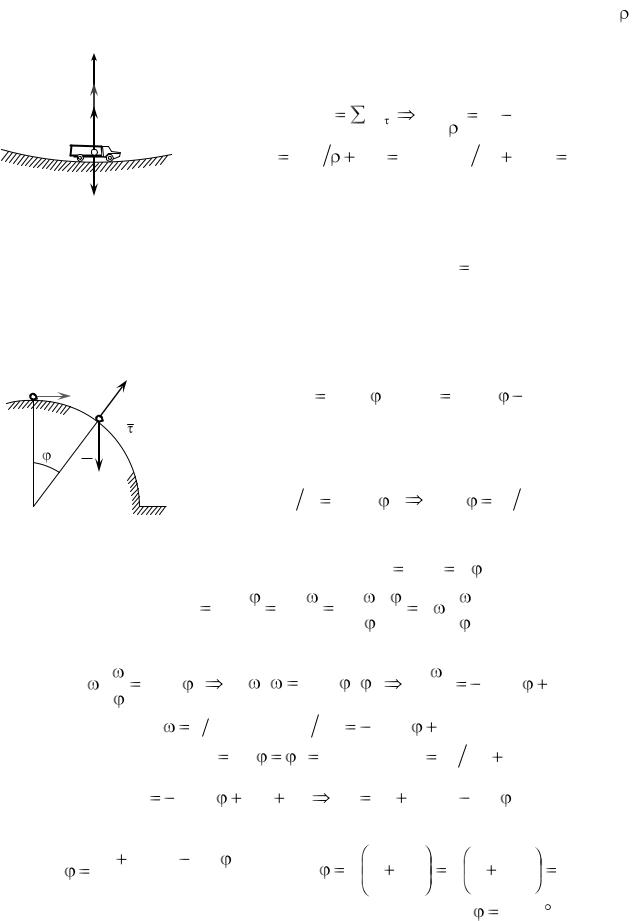
Пример 1.1. Лифт массой m начинает подниматься с y ускорением а. Определить натяжение троса (рис. 1.2).

Решение. На лифт действуют сила тяжести G и реакция троса T . Составим уравнение движения лифта вдоль оси y:

may	Fky	may	T G T G may	m(g a) .
Если лифт опускается вниз с таким же ускорением, то
натяжение троса:		may	T G T G may	m(g a) .

Рис. 1.2

Пример 1.2. Груз спускается вниз по негладкой наклонной плоскости, расположенной под углом к горизонту, двигаясь согласно уравнению x = at2, где а – постоянный коэффициент. Определить модуль силы трения скольжения

груза о плоскость (рис. 1.3).

Fтр

Решение. Показываем приложенные к грузу силы.

Составим дифференциальное уравнение движения груза

в проекции на ось х:

mg sin

Fт р .

(1)

Учитывая, что x at2 ,

откуда x

2at и x

2a . Тогда

из уравнения (1): Fт р mg sin

m(g sin

2a) .

Рис. 1.3

Пример 1.3. Груз в результате полученного толчка начал скользить вверх с

начальной скоростью

= 3

м/с

по

негладкой наклонной

плоскости,

расположенной под углом = 30° к горизонту. Определить путь s, пройденный грузом до остановки, если коэффициент трения скольжения равен f = 0.4.

Решение. Направим ось х в сторону движения груза, вверх, вдоль наклонной плоскости (рис. 1.4). Дифференциальное уравнение движения груза

вдоль оси х:

mg sin

Fтр ,

так как Fтр fN fmg cos

, тогда

g(sin

f cos )

gb .

Fтр

Проинтегрируем полученное ДУ,

заменив x

на dvx

dt и проставив пределы интегрирования:

dvx

gb dt

gbt .

(1)

Рис. 1.4

Из (1) найдем время движения груза до остановки vx

0 : t

gb .

(2)

Проинтегрируем (1) еще раз, заменив vx

на dx dt :

1 gbt2

gbt v

(

gbt

v )dt

v t .

Подставляя найденное время t (2), определим путь s пройденный грузом.

	v2	v2
s	0	0		0,542	м.
s	2gb 2g(sin		f cos )	0,542	м.
	2gb 2g(sin		f cos )

Рис. 1.6

Пример 1.4. Автомобиль массой m = 1000 кг движется по дну оврага с постоянной по модулю скоростью v = 90 км/ч. Определить давление автомобиля на дно оврага в наинизшей точке. Радиус кривизны траектории в этой точке равен 50 м (рис. 1.5). Силой сопротивления движению пренебречь.

Решение. Дифференциальное уравнение движения

материальной точки в проекции на главную нормаль:

man

N P .

Отсюда N

mv2

1000(252

50 9,81) 22310кг.

Сила давления автомобиля на дно оврага равна по

модулю N и направлена вниз.

Рис. 1.5

Пример 1.5. Шарику, находившемуся в вершине гладкой шаровой

поверхности радиусом R = 1 м, сообщена скорость v0

1 м/с. Определить, в

какой точке шарик отделится от поверхности и начнет двигаться свободно.

Решение. Шарик движется по гладкой шаровой поверхности под

действием двух сил:

силы тяжести

G и реакции поверхности N (рис. 1.6).

Уравнения движения шарика в естественных координатах (1.3):

О v0
	N

R n

m	d 2s	G sin	, m	v2	G cos N .
	dt2			R

Шарик отделяется от поверхности, когда реакция поверхности N равна нулю. Из второго уравнения при N = 0, получаем

mv2 R G cos

cos v2 gR . (1)

Для определения скорости в точке отрыва v воспользуемся первым уравнением. Начальное положение шарика примем за начало отсчета О дуговой координаты s. Тогда s OM R и распишем

d 2s

d 2

dt2

Подставляя в первое уравнение и интегрируя, получаем

g sin

R d

g sin d

g cos

C .

Учитывая, что

v R , имеем v2

g cos

C . Константу определим

по начальным условиям: v

v ,

0 . Откуда C

g .

g cos

2gR(1

cos

) .

Подставляя найденное v2 в уравнение (1), получаем

2gR(1

cos )

cos

или

cos

0,701.

9,81

Таким образом, шарик отделится от поверхности при угле

45,52 .

1.3.Задачи для самостоятельного решения

1)Материальная точка весом 49 Н движется по прямой согласно

уравнению x 8sin 2t см. Найти силу, действующую на точку в моменты времени, когда ее координата x = – 5 см.

Ответ: 1 Н и направлена к началу координат.

2)На вал диаметром 20 см намотана веревка, к свободному концу которой подвешен груз весом 800 Н. Угловая скорость вращения вала ω = 30t c-1. Определить натяжение веревки, когда груз: а) поднимается; б) опускается.

Ответ: а) 1045 Н; б) 555 Н.

3)Определить давление человека весом 0.85 кН на площадку лифта в начале подъема и перед остановкой, если ускорение (замедление) равно 0.4g.

Ответ: 1.19 кН; 0.51кН.

4)Материальная точка весом 49 Н движется по горизонтальной окружности радиуса 9 см согласно уравнению s = 8t3 см. Определить величину

инаправление силы F, действующей на эту точку в момент t = 1 c.

Ответ: F = 4 H; 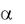arctg(3/ 4) .

5)	Материальная	точка	массой 300 г движется согласно уравнению:
x 3cos	t см, y 3sin	t , z	5t см. Найти силу, действующую на эту точку.

Ответ: F = 0.089 Н.

6) Определить максимальную скорость велосипедиста на закруглении дороги радиуса 50 м, если коэффициент поперечного трения между шинами


велосипеда и асфальтом f = 0.4. Определить, на какой		угол	отклонилась
плоскость велосипеда от вертикальной плоскости.		Полотно дороги
расположено в горизонтальной плоскости. (v = 14 м/с;	arctgf		21 50 ).

7)На криволинейных участках автодороги возвышают наружную сторону над внутренней для того, чтобы сила давления проезжающего автомобиля была перпендикулярна дороге. Определить угол наклона полотна дороги, если

радиус закругления 1000 м, максимальная скорость автомобиля 120 км/ч.

Ответ: 6,46 .

8)Груженая вагонетка массы 700 кг опускается по канатной железной

дороге с уклоном 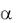15 , имея скорость v 1,6 м/с. Определить натяжение каната при равномерном спуске и при торможении вагонетки. Время торможения t = 4 c, общий коэффициент сопротивления движению f = 0.015. При торможении вагонетка движется равнозамедленно. (1676 Н, 1956).

9)Грузовой автомобиль массы 6000 кг въезжает на паром со скоростью 6 м/с. Заторможенный с момента въезда на паром автомобиль остановился, пройдя 10 м. Считая движение автомобиля равнозамедленным, найти натяжения каждого из двух канатов, которыми паром привязан к берегу. При решении задачи пренебречь массой и ускорением парома.

Ответ: Натяжение каждого каната 5400 Н.

10)На материальную точку массой 200 г, движущуюся вдоль горизонтальной оси Ох, действует постоянная сила F = 2 H. В начальный

момент x0 = 3 м, v0 = 4 м/с. Найти уравнение движения точки. ( x 5t2 4t 3).

11) Хоккеист сообщает шайбе прямолинейное движение по ледяному полю. Чему была равна начальная скорость шайбы, если она прошла до остановки 50 м? За какое время шайба прошла это расстояние, если коэффициент трения шайбы о лед f = 0.05? Сопротивлением воздуха пренебречь.

Ответ: v0 7 м/с, t = 14,3 м/с.

12) Коэффициент трения лыж о снег при движении лыжника по склону горы вниз f = 0,1. Угол склона 60°, а его длина 100 м. Определить время спуска и скорость лыжника в конце склона, если в начале спуска она была равна нулю.

Сопротивлением воздуха пренебречь. ( t			5 с, v = 40 м/с).
	13) Управляемый снаряд, поднявшись на высоту 20 км, движется дальше
как	свободное	тело в безвоздушном	пространстве	с	начальной	скоростью
v0	1700 м/с,	составляющей с горизонтом угол =		45°. Определить время,
дальность полета и высоту траектории снаряда. (280с, s					306 км, H	106,4 км).
	14) После вертикального запуска управляемый снаряд движется по
траектории с начальной скоростью v0			1700 м/с, наклоненной под углом 45° к

горизонту. Определить высоту подъема снаряда перед выходом на траекторию, если дальность его полета L = 300 км. Сопротивлением воздуха пренебречь.

Ответ: H L(gL / v2	1) 5,5км.
0

15) Какую начальную скорость v0 легкоатлет должен сообщить ядру,

брошенному с высоты 2 м над землей под углом 45° к горизонту, чтобы оно пролетело расстояние 18 м? Сопротивлением воздуха пренебречь. (12,6).

16) Под каким углом 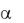к горизонту надо выстрелить из орудия, поставленного в начале координат, чтобы попасть в цель, координаты которой

x = 1 км, y = 0,5 км, если		начальная скорость снаряда v0 1000 м/с?
Сопротивлением воздуха пренебречь. Ось Оy направлена вверх.
Ответ:	26 50 .
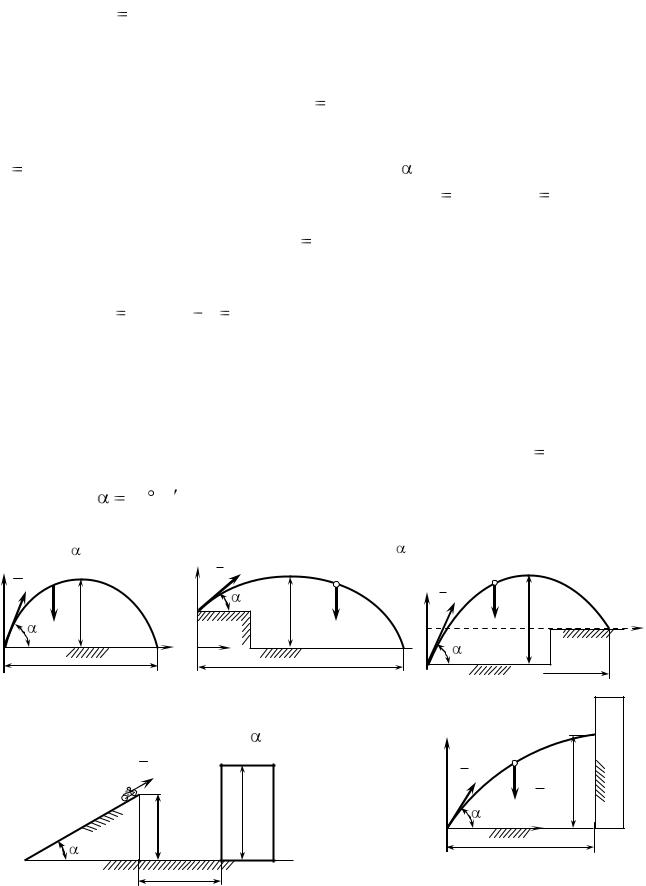
17) Миномет выстреливает мину М c начальной скоростью v0:
Даны: v0, . Найти: H, L.		Даны: ±y0, v0, . Найти: H, L.

у v0 М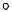

mg H

0	L

у v0

		H		у	v0	H
		H	mg	0	mg	H
		х		0		х
	0	х

х			L			L
						L

18) С какой скоростью должен вылететь с трамплина каскадер на мотоцикле, чтобы приземлиться на здание В, если = 30°?

v0
	В
30 м	40 м
	20 м

Даны: v0, l, h. у Найти: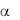

v0	М
v0	mg	h
	mg
0	х	l
		l

2. Общие теоремы динамики материальной точки

2.1. Теорема об изменении количества движения точки

Полным импульсом силы

F ,

действующей на материальную точку в

течение времени t, называется вектор

Fdt .

Проекции полного импульса силы F на оси декартовых координат:

Fxdt , Sy

Fy dt , Sz

Fz dt .

Модуль и направление полного импульса S определяются по проекциям:

Sx2

Sy2 Sz2 ; cos(

,i )

S , cos(S , j) Sy

S , cos(S , k )

Sz S .

Количеством движения материальной точки называется векторная

величина mv , равная произведению массы точки m на ее скорость v .

Запишем ДУ (1.1) движения материальной точки М в виде mdv dt

или, так как

const,

d (mv)

(2.1)

Уравнение (2.1) выражает теорему об изменении количества движения

точки в дифференциальной форме. Перепишем (2.1)

в виде d(mv)

Fdt

проинтегрируем ДУ в пределах от 0 до t:

d (mv )

Fdt ,

mv0

М1

mv1

mv0

(2.2)

М0

mv0

где v , v0

– абсолютная скорость

точки в текущий


	начальный моменты времени соответственно; S – полный			Рис. 2.1
	импульс равнодействующей силы за время t (рис. 2.1).			Рис. 2.1
	импульс равнодействующей силы за время t (рис. 2.1).
	Уравнение (2.2) выражает теорему об изменении количества движения

точки в интегральной форме: изменение количества движения точки за промежуток времени от 0 до t равно полному импульсу равнодействующей силы, действующей на точку, за тот же промежуток времени. В проекциях на оси

mvx mv0 x

Sx ;

mvy mv0 y

Sy ;

mvz

mv0 z

(2.3)

2.2. Теорема об изменении момента количества движения точки

Моментом количества движения материальной точки относительно

некоторого центра О называется векторная величина

Lxi Ly j Lz k m0 (mv ) r mv ,

Lx m( yvz

zvy ) , Ly

m(zvx

xvz ) , Lz

m(xvy

yvx ) ,

0 , если

где r – радиус-вектор движущейся точки.

смотря навстречу оси

х,

движение точки происходит

против хода часовой стрелки. Когда Lx

– наоборот.

Рис. 2.2

Модуль вектора L0 равен L0 mvh

Lz .

Запишем уравнение движения материальной точки

dL0

(2.4)

mdv dt F r m

r F

(r mv ) r F

Уравнение (2.4) выражает теорему об изменении момента количества движения точки: первая производная по времени от момента количества движения точки относительно центра О равна моменту равнодействующей силы относительно того же центра О. В проекциях на оси координат имеем

	dL			dLy			dL
	x	M x ,				M y ,	z	M z	.
	dt	M x ,		dt		M y ,	dt	M z	.
	dt			dt			dt
			2.3. Работа силы

Пусть точка приложения силы					F перемещается по криволинейной
траектории из положения M 0			в положение M1 . Разобьем перемещение точки М

по дуге M 0M1 на бесконечно малые перемещения ds и определим работу на каждом таком перемещении (рис. 2.3).

Элементарной работой силы F , приложенной в точке М, называется скалярная величина равная произведению элементарного перемещения на

проекцию силы на это перемещение.

F ds

F cos ds

(2.5)

Поскольку

то

(2.5) запишется

М1

М0

cos

Fxdx

Fy dy

Fz dz .

Рис. 2.3

Полную работу силы F на перемещении точки из положения М0 в положение М1 определяют как предел интегральной суммы соответствующих элементарных работ

M1	M1	M1
A dA	F ds	(Fxdx Fydy Fz dz)	.	(2.6)
M0	M0	M0

Пример 2.1. Найти импульс равнодействующей всех сил, действующих на снаряд за время, когда снаряд из начального положения О переходит в

наивысшее положение М (рис. 2.4). Известно: v0 500 м/с;

60 ;

v1 200 м/с; масса снаряда 100 кг.

Решение. По теореме об изменении количества движения точки (2.3):

у	М	v1		mv1x	mv0 x		Sx ,
v0				mv	mv	0 y	S	y	.
				1y		0 y		y
				Применительно к рис. 2.4, имеем
О	L		х	mv1	mv0 cos				Sx ,
				mv1	mv0 cos				Sx ,
				0 mv0 sin			S y .
	Рис. 2.4			0 mv0 sin			S y .
	Рис. 2.4
				Подставляя			числовые значения,
находим: Sx	m(v1	v0 cos )	5000 Н∙с, S y		v0msin				43301 Н∙с.

Пример 2.2. По шероховатой наклонной плоскости, составляющей с горизонтом угол = 30°, спускается тело без начальной скорости. Определить, в течение какого времени t тело пройдет путь длины l = 40 м, если коэффициент трения f = 0.1 (рис. 2.5).

Решение. Теорема об изменении количества движения вдоль оси х и у:

mvx

mv0 x

Fkx t,

mvx

(mg sin

Fтр ) t,

mvx

(mg sin

Nf ) t,

mvy

mv0 y

Fky t.

mg cos

) t.

mg cos .

Подставляя N в первое уравнение системы и

Fтр

сокращая на m, находим закон изменения скорости

g(sin

f cos

) t ,

) t2 / 2 .

g(sin

f cos

Отсюда t

2l / g(sin

f cos

)

4.95 с.

Рис. 2.5

Пример 2.3. Материальная точка массы m движется по эллиптической траектории вокруг неподвижного центра под действием центральной силы.

Найти скорость в точке А, если скорость в точке В равна vB

30 м/с,

а малая

полуось эллипса b = 5a (рис. 2.6).

Решение. Согласно

теореме

об изменении

момента количества движения точки

0 , в

нашем случае

M z

0 , так как сила центральная

(линия действия силы проходит через центр О).

Следовательно,

const

или LzA

LzB

отсюда

mvAa

mvBb

vBb / a

600 м/с.

Рис. 2.6

2.4. Задачи для самостоятельного решения

Модуль

постоянной по направлению силы изменяется по закону

F 8t2

Найти модуль импульса этой силы за промежуток времени

t1 , где t2

2 с, t1

0 . (34 Н∙с).

2) На материальную точку массой 10 кг действует сила постоянного

направления, значение которой изменяется по закону

5t3 . Определить

скорость этой точки в момент t = 2 c, если v0

3 м/с.

Ответ: 5 м/с.

3) Материальная точка массой 5 кг движется по прямой под действием

постоянной силы F (схема предыдущей задачи). Скорость токи за промежуток

времени t

t1,

где t2

10 с, t1

0 изменилась от v1

5 м/с до v2

15 м/с.

Определить модуль силы F . (5 Н).

4) С какой начальной скоростью брошен камень под углом 30º к горизонту, если до падения его на землю прошло 2.5 с? Чему равна минимальная скорость камня во время его движения? Сопротивлением воздуха пренебречь.

Ответ: v0 = 24,5 м/с, vmin = 21,2 м/с.

1 / 41 2 3 4 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
11.05.201516.38 Кб32С1.docx
#
11.05.2015537.09 Кб76С1_0.doc
#
11.05.2015441.34 Кб239С1_1.doc
#
11.05.2015684.54 Кб91С4.doc
#
11.05.201524.82 Mб102сборка.docx
#
17.03.20161.79 Mб205сборник задач по динамике.pdf
#
17.03.201634.08 Кб13Сваи. БЖД.docx
#
12.05.2015508.58 Кб27СВАРКА+.pdf
#
11.05.2015471.04 Кб66Секвестор (1).doc
#
11.05.2015428.54 Кб21силикаты пояснилка.doc
#
11.05.201565.55 Кб21силикаты.docx