
- •Введение
- •Глава 1. Элементы векторного анализа
- •1. Векторы и действия над ними
- •2. Математическое понятие поля. Градиент
- •3. Дивергенция. Теорема Остроградского-Гаусса
- •4. Ротор. Теорема Стокса
- •5. Некоторые соотношения векторного анализа
- •6. Операции в криволинейных координатах
- •В цилиндрических координатах
- •В сферических координатах
- •7. О дифференциальных уравнениях с частными производными
- •Глава 2. Уравнения лапласа и пуассона
- •8. Дельта-функция Дирака
- •9. Интегрирование уравнения Пуассона
- •10. Граничные задачи для уравнения Лапласа
- •11. Метод разделения переменных
- •Глава 3. Гармонические колебания и волны
- •12. Гармонические колебания и метод комплексных амплитуд
- •13. Волновые процессы и их математическое описание
- •14. Вращение декартовой системы координат
- •Глава 4. Решения волновых уравнений
- •15. Интегрирование неоднородного уравнения Гельмгольца и уравнения Даламбера
- •16. Уравнение Бесселя и цилиндрические функции
- •17. Решение однородного уравнения Гельмгольца методом разделения переменных
- •Глава 5. Краевые задачи электродинамики
- •18. Граничные задачи для уравнения Гельмгольца.Собственные функции и собственные значения
- •19. Ортогональные системы функций и ряды Фурье
- •20. Сведения из алгебры
- •21. Проекционные методы
- •Список литературы
- •Контрольные задания
Глава 2. Уравнения лапласа и пуассона
В уравнения Максвелла входят
плотность заряда ρ
и плотность тока проводимости
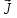 ,
а также другие функциями плотности,
например, плотности мощностиp,
плотности энергии ω
и т. д. Эти функции
определяются предельными выражениями,
которые имеют вполне ясный смысл при
плавно меняющихся, как говорят, гладких
(дифференцируемых) распределениях
заряда, тока и иных физических величин.
Но как, например, охарактеризовать при
помощи функции ρ идеальный точечный
заряд, который занимает исчезающе малый
объем, а, следовательно, должен иметь
бесконечную плотность в точке? На этот
и подобные вопросы, касающиеся дискретных
распределений, дает ответ аппарат
дельта-функции Дирака. Этот аппарат
будет использован, в частности, при
интегрировании уравнения Пуассона.
,
а также другие функциями плотности,
например, плотности мощностиp,
плотности энергии ω
и т. д. Эти функции
определяются предельными выражениями,
которые имеют вполне ясный смысл при
плавно меняющихся, как говорят, гладких
(дифференцируемых) распределениях
заряда, тока и иных физических величин.
Но как, например, охарактеризовать при
помощи функции ρ идеальный точечный
заряд, который занимает исчезающе малый
объем, а, следовательно, должен иметь
бесконечную плотность в точке? На этот
и подобные вопросы, касающиеся дискретных
распределений, дает ответ аппарат
дельта-функции Дирака. Этот аппарат
будет использован, в частности, при
интегрировании уравнения Пуассона.
Рассмотрение граничных задач для уравнения Лапласа понадобится для правильного суждения о содержании важных классов задач электростатики.
Наконец, излагаемый в данной главе метод разделения переменных применяется далее к самым различным задачам теории электромагнетизма.
8. Дельта-функция Дирака
8.1. Первоначальное понятие. Рассмотрим функцию F(x), изображаемую в виде «импульса»:
F(х) = 0 при х < - Δх и при х > Δх, причём
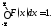 (8.1)
(8.1)
Введём новую функцию δ(х) как предел
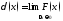 (8.2)
(8.2)
В частности, при задании F(x) в виде прямоугольного импульса она равна:
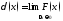
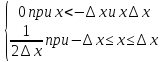 (8.3)
(8.3)
Функция δ (х), как видно, равна нулю везде кроме исчезающе малой окрестности точки х = 0, где она неограниченна. С точки зрения классического математического анализа, рассмотрение δ(х) затруднительно, следовало бы сказать, что предел (8.2), (8.3) не существует.
Тем не менее, произведенные рассуждения наводят на мысль о существовании особого математического объекта, называемого дельта-функцией Дирака (по имени известного физика). В качестве определения дельта-функции δ(х) обычно рассматривают следующее интегральное соотношение
 (8.4)
(8.4)
где f(x) - обычная функция. При этом для всякого ограниченного отрезка
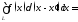
 (8.5)
(8.5)
В частности, при f(x) = 1
 (8.4а)
(8.4а)
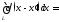
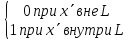 (8.5а)
(8.5а)
Вернёмся теперь к формулам
(8.1) - (8.3), чтобы убедиться, что интуитивный
образ, к которому они приводят,
соответствует определению дельта-функции.
Согласно (8.2), (8.3) δ(х)
= 0 везде кроме точки
х =
0 (соответственно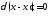 везде кроме точки
везде кроме точки
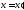 при сохранении
интеграла (8.1). Это отвечает соотношениям
(8.4 а), (8.5 а). Что касается формул (8.4) и
(8.5), то всю область интегрирования, когда
она включает точку х΄
можно заменить отрезком
ΔL,
покрывающим х'
и настолько малым, что функцию f(x)
на нем можно считать
постоянной и равной f(x').
Поэтому
при сохранении
интеграла (8.1). Это отвечает соотношениям
(8.4 а), (8.5 а). Что касается формул (8.4) и
(8.5), то всю область интегрирования, когда
она включает точку х΄
можно заменить отрезком
ΔL,
покрывающим х'
и настолько малым, что функцию f(x)
на нем можно считать
постоянной и равной f(x').
Поэтому
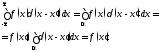 .
.
8.2. Обобщение и примеры. Всё cказанное нетрудно обобщить, например, на функцию трёх переменных. Взяв вместо отрезка L пространственную область V, будем обозначать задаваемые нам функции как /(г) (§ 2, п. 1). Аналогично (8.1) можно рассматривать функцию F(r) такую, что
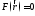 при
при
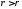
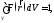
и
в том же смысле, что
и в (8.2), говорить о предельном случае

Переходя к определению
дельта-функции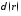 ,
вместо (8.4) и (8.5) будем
иметь:
,
вместо (8.4) и (8.5) будем
иметь:
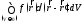 (8.6)
(8.6)
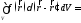
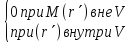 (8.7)
(8.7)
Подобным же образом рассматривается и двумерный случай. Достаточно лишь вместо V взять S; тогда r лежит в плоскости, на которой лежит область S и круг радиуса ρ.
Разумеется, в трехмерном случае (при использовании декартовых координат) справедливо равенство:
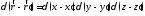 , (8.8)
, (8.8)
и аналогичное равенство можно записать для двумерного случая.
В качество примера применения
дельта-функции
 охарактеризуем
плотность заряда
охарактеризуем
плотность заряда
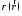 в
пространстве при наличии точечного
зарядаq,
расположенного в
точке М
в
пространстве при наличии точечного
зарядаq,
расположенного в
точке М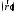 .Легко видеть, что
.Легко видеть, что
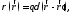 (8.9)
(8.9)
так как при этом
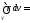
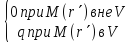 (8.10)
(8.10)
Возьмём, далее, некоторую
поверхность S
(рис. 8.2), пусть на ней заданы координатные
функции q1,
q2
(криволинейные
координаты, см. п. 6.1) и нормаль
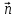 ,
которую мы представляем как прямолинейную
координату с началом наS
(n
= 0 на S);
если S
несёт поверхностный заряд с плотностью
,
которую мы представляем как прямолинейную
координату с началом наS
(n
= 0 на S);
если S
несёт поверхностный заряд с плотностью
 ,
его можно рассматривать как распределённый
в объёме с плотностью
,
его можно рассматривать как распределённый
в объёме с плотностью
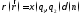 (8.11)
(8.11)
Действительно,
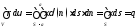
(точки а
и -а
лежат на прямой n
по разные стороны S).
Рассмотрим поверхностный ток I,
распределенный на Р
сплотностью
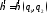 .Вместо
.Вместо
 можно ввести плотность
тока в объёме
можно ввести плотность
тока в объёме
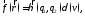 (8.12)
(8.12)
где подразумевается, что
точки
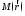 находятся
на какой-либо поверхностиS,
пересекающей Р по
линии l,
a
n
- координатная линия
в S.
находятся
на какой-либо поверхностиS,
пересекающей Р по
линии l,
a
n
- координатная линия
в S.
В самом деле, при этом
пересекающий
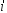 поверхностный ток описывается как ток
в объёме с плотностью
поверхностный ток описывается как ток
в объёме с плотностью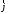 ,
проходящей черезS:
,
проходящей черезS:
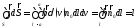
(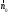 - орт нормали к l,
касательный Р).
- орт нормали к l,
касательный Р).
Наконец, возьмём случай тока I, протекающего, вдоль, линии L. Для такого линейного тока
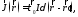 (8.13)
(8.13)
где
дельта-функция двумерная; соответственно
этому точки
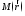 -и
-и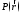 (последняя лежит на
L)
при интегрировании
остаются на какой-либо поверхности,
пересекаемой током.
Вычисляя ток I,
имеем:
(последняя лежит на
L)
при интегрировании
остаются на какой-либо поверхности,
пересекаемой током.
Вычисляя ток I,
имеем:
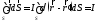
8.3. Представление дельта-функции δ (r). Взяв функцию
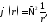
убедимся; что везде, за исключением точки r = 0, она равна нулю. Действительно, на основании (6.21) .
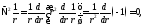

Исследуем теперь объёмный
интеграл от
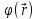 по области V,
содержащей начало
координат r
= 0; при помощи теоремы
Остроградского-Гаусса преобразуем его
к поверхностному:
по области V,
содержащей начало
координат r
= 0; при помощи теоремы
Остроградского-Гаусса преобразуем его
к поверхностному:

Пусть V
- сферический объём с центром при r
= 0; тогда S
есть соответствующая сферическая
поверхность радиуса ρ,
накоторой функция grad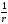 постоянна и согласно (6.18) или(2.12а)
равна:
постоянна и согласно (6.18) или(2.12а)
равна:
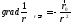
Таким образом, для любого сферического (а, следовательно, и иного) объема V, содержащего начало координат,
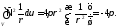
Подведём итог. Функция
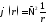 ,
равная нулю везде, кроме начала координат,
при интегрировании по любой области,
включающей начало, даёт - 4π. Поэтому,
будучи умножена на -1/4π,
эта функция удовлетворяет
определению (8.6), (8.7). Это значит, что
найдена дельта-функция
,
равная нулю везде, кроме начала координат,
при интегрировании по любой области,
включающей начало, даёт - 4π. Поэтому,
будучи умножена на -1/4π,
эта функция удовлетворяет
определению (8.6), (8.7). Это значит, что
найдена дельта-функция
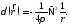 (8.14)
(8.14)
Очевидно также, что
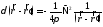 (8.14а)
(8.14а)
Полученный результат ниже будет использован при интегрировании уравнения Пуассона.
